ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Neelam Kumari1, Seema Mehra2 Department of mathematics, M. D. University Rohtak (Haryana), India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper a new labeling known as n-edge magic labeling is introduced. Let G (V, E) be a graph, where V and E represents the set of vertices and edges respectively .We denote the graph G by G (p, q) , having p vertices and q edges. Graph, graph labeling, magic labeling, edge magic labeling, vertex magic labeling, 0-edgemagic labeling and 1-edge magic labeling have been discussed. It is proved that some graphs such as Pn, Cn (n being odd +ve integer) and many other graphs have n-edge magic labeling. In this paper the problem of graphs having n- edge magic labeling is studied.
Keywords |
| Graph, Graph Labeling, Edge Labeling, Edge Magic Labeling, 0-Edge Magic Labeling, 1- Edge Magic Labeling. |
INTRODUCTION |
| All graphs in this paper are finite, simple, planer and undirected. The graph G has the vertex set V (G) and edge set E (G). A labeling of a graph G is a mapping that carries graph elements to integers. The origin of this labeling is introduced by Rosa. We deal with labeling having domain either the set of all vertices, or the set of all edges, or the set of all vertices and edges, respectively. We call these labeling a vertex labeling, or an edge labeling, or a total labeling, depending on the graph elements that are being labeled. In this paper, we focus on one type of labeling called n- edge magic labeling. |
| The concept of labeling of graphs has gained a lot of popularity in the area of graph theory. This popularity is not only due to mathematical challenges of graph labeling but also to the wide range of applications that graph labeling offer to other branches of science, for instance, X-ray, crystallography, coding theory, cryptography, astronomy, circuit design and communication networks design. In the last three decades magic and antimagic labeling, prime labeling, graceful labeling, k-graceful labeling, and odd labeling, even and odd mean labeling and strongly labeling etc. have been studied in over 1300 papers. Recently in 2012, J. Jayapriya and K.Thirusangu introduced 0-Edge Magic Labeling and shown the existence of this labeling for some class of graphs. Motivated by 0-Edge Magic Labeling we have introduced n-Edge Magic Labeling for certain graphs as for Pt, Ct , Sm,t (i.e. double star) etc. Now we shall drive the existence of n-edge magic labeling for some graphs. |
PRELIMINARY |
| In this section we give some basic definitions of vertex labeling and edge labeling. |
| Definition 2.1 The vertex-weight of a vertex v in G under an edge labeling is the sum of edge labels corresponding to all edges incident with v. Under a total labeling, vertex-weight of v is defined as the sum of the label of v and the edge labels corresponding to the entire edges incident with v. If all the vertices in G have the same weight k, we call the labeling vertex-magic labeling or vertex-magic total labeling respectively and we call k a magic constant. If all the vertices in G have different weights, then the labeling is called vertex-antimagic edge labeling or vertex antimagic total labeling. |
| Definition 2.2 The edge- weight of an edge e under a vertex labeling is defined as the sum of the vertex labels corresponding to every vertex incident with e, under a total labeling, we also add the label of e. Using edge –weight, we drive edge magic vertex or edge magic total labeling and edge-antimagic vertex or edge antimagic total labeling. |
| Definition 2.3 A (p, q) graph G is said to be (1 ,0) edge-magic with the common edge count k if there exist a bijection f:V(G)→{1,2,…………p} such that for all e=uv E(G), f(u)+f(v)=k. It is said to be (1, 0) edge-antimagic if for all e = uv E (G), f (u) +f (v) are distinct. |
| Definition 2.4 A (p, q) graph G is said to be (0, 1) vertex –magic with the common vertex count k if there exist a bijection f : E(G)→ {1, 2,…………q } such that for each u V(G), Σ f(e)=k, where e E(G) and e is incident on u. It is said to be (0, 1) vertex-antimagic if all the weights are distinct. |
| Definition 2.5 A (p, q) graph G is said to be (1, 1) edge-magic with the common edge count k if there exist a bijection f : V(G)UE(G) → {1,2,…………….. p + q} such that f(u) + f(v) + f(e) =k for all e=uv E (G). It is said to be (1, 1) edge antimagic if f (u) +f (v) +f (e) are distinct for all e = uv E (G). |
| Definition 2.6 Let G =(V, E) be a graph , V={vi ,1≤ i≤ t} and E = {vi vi+1 , 1 ≤ i ≤ t-1}. Let f : V →{-1, 1} and f* : E→ {0}, such that for all uv E, f* (u v) =f(u)+f(v)=0 then the labeling is said to be 0-Edge Magic labeling. |
| Definition 2.7 G + =GÃÅ ÃËK1 is a graph obtained by joining exactly one pendant edge to every vertex of a graph G. |
| Definition 2.8 A sun St is a cycle on t vertices with an edge terminating in a vertex of degree 1 attached to each vertex on the cycle. |
| Definition 2.9 A complete binary tree T is a tree with a central vertex of degree 2 , all other vertices that are not leaves of degree 3, and all leaves at the same distance from the central vertex. |
| Definition 2.9 Let G= (V, E) be a graph where V= {vi, 1 ≤ i ≤ t} and |
| E = {vi v i+1,1≤i≤ t-1} |
MAIN RESULTS |
| The concept of 0-Edge Magic Labeling and 1-edge magic labeling motivate us to define the following new definition of n-Edge Magic Labeling. |
| n-Edge Magic Labeling : Let G=(V, E) be a graph where V= { vi, 1≤i≤ t } and |
| E = {vi v i+1,1≤i≤t-1} |
| Let f: V → {-1, n+1} and f*: E → {n} such that for all uv E, f*(u v) = f (u) + f (v) = n then the labeling is said to be n-Edge Magic Labeling. |
| Using this new definition, we prove some results as follows: |
| Theorem 3.1 Pt admits n-Edge Magic Labeling for all t. |
| Proof: Let G = (V, E) be a graph where V= {vi , 1≤i≤ t} and E = {vi v i+1, 1≤i≤ t-1}. |
| Let f: V → {-1, n+1} |
| Such that f (vi) = -1 if i is odd. |
| f (vi +1 ) = n+1 if i is even |
| for 1≤i≤ t, we have |
| f* (v i. v i+1 ) = -1+(n+1) = n if i is odd. |
| f* (v i. v i+1 ) = (n+1) -1 = n if i is even |
| Hence pt admits n-Edge Magic Labeling. |
| Theorem 3.2 C t admits n-Edge Magic Labeling when t is even. |
| Proof: Let G =(V, E) be a graph where V={vi : 1 ≤ i ≤ t} and E={ vi. vi+1 , 1 ≤ i ≤ t-1 |
| Let f; V→{-1,n+1 }such that |
| f (v i)= -1 if i is odd |
| f(v i)= n+1 if i is even |
| for 1≤i≤t, we have |
| f * (v i. v i+1 ) = -1+(n+1)= n if i is odd, |
| f* (v i. v i+1 ) = (n+1)-1= n if i is even. |
| Hence C t admits n-Edge Magic Labeling for every even t. |
| Corollary: 1 Similarly we can prove that the graph mC t is n-edge magic for all m and even t. |
| Theorem 3.3 A sun graph St is n-edge magic only when t is even. |
| Proof: Let v1, v2, ……….. vt be the vertices of cycle St and u1, u2, …….ut be the end vertices of each edge attached to v1, v2, ……….. vt. |
| f(vi)= -1 if i is odd, |
| f(vi)= n+1 if i is even. |
| and |
| f (ui)= -1 if f(vi)=n+1, |
| f (ui)= n+1 if f(vi)= -1. |
| for 1≤i≤t, we have |
| f * (v i. v i+1 ) = -1+(n+1)= n if i is odd, |
| f* (v i. v i+1 ) = (n+1)-1= n if i is even. |
| And f * (v i. u i ) = -1+(n+1)= n if i is odd, |
| f* (v i. u i) = (n+1)-1= n if i is even. |
| This completes the proof. |
| Example 1: To support the Theorem 3.4 we give an example of n-Edge Magic Labeling for S6. |
| Solution: |
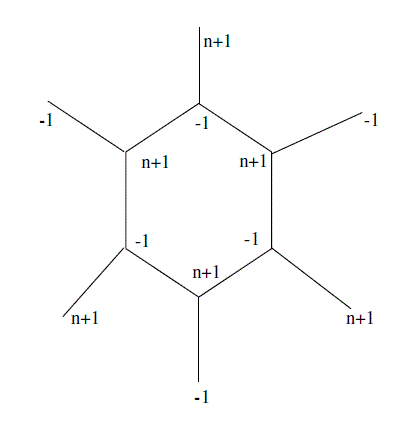 |
| Theorem 3.4 If G admits n-Edge Magic Labeling then GÃÅ ÃËK1 admits n-Edge Magic Labeling. |
| Proof :- Let G=(V, E) be a graph where V={ v i : 1 ≤ i≤ t} and E={ v i. v i+1 , 1 ≤ i ≤ t-1}. |
| Let f: V→{-1, n+1 } and f* : E→{n} such that for all v i. v i+1 E |
| f* (vi. vi +1 ) = f (vi)+ f (vi+1) = n |
| Let |
| GÃÅ ÃËK 1 = (V ,E) U { v ÃâÃË : 1 ≤ j ≤ t } U { vi. vÃâÃË: 1 ≤ i,j ≤ t }, then let g: V→{-1, n+1} and g* : E→{n} , then for all vi. vi+1 E |
| Let vÃâÃË = -1 if vi = n+1 or vÃâÃË = n+1 if vi = -1 then g*( vi v ÃâÃË) = g*( vi)+ g*( v ÃâÃË) = n |
| Hence the theorem. |
| Example 2: To support the Theorem 3.4 we give example of n-Edge Magic Labeling for P4ÃÅ ÃËK1 |
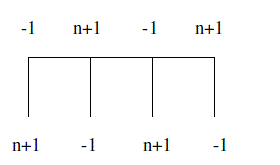 |
| Theorem 3.5: Let G =S m, t be a double star graph then G admits n-Edge Magic Labeling. |
| Proof: Let G = (V, E) be a double star graph denoted by Sm, t and v1 and v2 are two vertices in Sm,t which are not pendent. Let ui ’ s are m pendent vertices to vi and uj ’ s are t pendent vertices to v2. |
| Let |
| f: V→{-1 , n+1} |
| such that f (v1)= -1 and f ( v2)= n+1, |
| and f(ui ) = n+1 for 1 ≤ i ≤ m, |
| and f(u j )= -1 for 1 ≤ j ≤ t. |
| f *(v1 ui ) = -1 + (n+1)= n if 1 ≤ i ≤ m, |
| Also f *(v2 u j ’ ) = (n+1) - 1 = n if 1 ≤ j ≤ t. |
| Hence the proof. |
| Corollary: using the above theorems we can prove that Ladder, Wheel graph and Kt admits n-edge magic labeling if t≡0 (mod 2), either t is even. |
| In this paper we have investigated some class of graphs which admits n-Edge Magic Labeling. Further investigation can be done to obtain the conditions at which some graphs admits n-Edge Magic Labeling. |
References |
|