Stochastic Generation and Forecasting Of Weekly Rainfall for Rahuri Region

Abstract

One of the major problems in water resources management is the advanced knowledge of future sequences of rainfall or rainfall forecast. With the effect of rainfall on water resources as a foregone conclusion, more accurate prediction of rainfall would enable more efficient of water resources. Regions depending on agro-based economy could benefit tremendously from accurate rainfall predictions. This study, is therefore, particularly focused on rainfall forecasting and generation since a forecasting could provide better information for optimal management of a resource over a substantial period of time. There are several techniques of rainfall forecasting that include autoregressive (AR) and moving average (MA) models of different orders, ARMA, ARIMA, Thomas Feiring etc. These are also called as stochastic or time series models. Autoregressive integrated moving average (ARIMA) models have been found to be more useful for forecasting and generation of hydrological events. Therefore, in this study ARIMA models of different orders have been used for generation and forecasting rainfall in advance. The present study attempts to develop the ARIMA model for forecasting and generation of weekly rainfall. Data were collected from National Data Centre of India Meteorological Department, Pune. Rainfall data series of 31 years (1982 – 2012) of Rahuri region of Ahmednagar district were used for developing ARIMA models. The series of 30 years i.e. from 1982 to 2011 was used for the development of the models and series of 2012 was used for testing the validity of the models. ARIMA models of different orders were selected based on observing autocorrelation functions (ACF) and partial autocorrelation functions (PACF) of the historical rainfall series. The parameters of selected model were obtained with the help of maximum likelihood method. The diagnostic checking of the selected models was then performed with the help of three test (standard error of parameters, ACF and PACF of residuals and Akaike Information Criteria) to know the adequacy of the selected models. The ARIMA models that passed the adequacy test were selected for forecasting. The weekly rainfall values 2012 year were forecasted with the help of these selected models and compared with the actual weekly rainfall values of the year 2012 by root mean square error (RMSE). The ARIMA (1,1,1) (1,0,1) 52 gave the lowest value of RMSE and hence is considered as the best model for generation and forecasting of weekly rainfall values.

Keywords

Stochastic model, ARIMA, Rainfall forecasting and Generation

INTRODUCTION

Water is limited resource and its efficient use is basic to the survival of the ever increasing population of the world. The basic source of water is the precipitation in the form of rainfall or snowfall and is the most critical and key variable of hydrological cycle. The major source of water for agriculture and human consumption is direct or stored (above ground, underground and or soil zone) rainfall.

Rainfall is a crucial agroclimatological factor in the seasonally arid parts of the world and its knowledge is an important perquisite for agricultural planning [1]. India is a tropical country and its agricultural depends on monsoon rainfall. More than 75% of rainfall occurs during the monsoon season. However monsoon rainfall is uneven both in time and space and

hence pose great deal of challenges for analysis including forecasting and generation. Maharashtra state, the major portion of which lies in semi arid tropics lies between 15 44’ and 21 40’ N latitudes and 73 15’ and 80 33’ E longitudes. This state forms a major part of Indian peninsula with a geographical area about 30.75 mha; out of which cultivable area is 22.5 mha. Summer, rainy and winter seasons are three distinct seasons in Maharashtra. The rainfall varies from 400 mm to 6000 mm with an average precipitation of 1433 mm. The variability of rainfall in state is high and it affects the agricultural production and the economy of the state. Thane, Raigad, Ratnagiri and Sindhudurg districts, receive heavy rains of an average of 2000 mm annually. But the districts of Nasik, Pune, Ahmednagar, Dhule, Jalgaon, Satara, Sangli, Solapur and parts of Kolhapur get rainfall less than 500 mm. Thus rainfall particularly concentrates to the Konkan and Sahyadrian Maharashtra. Central Maharashtra receives less rainfall. However, under the influence of the Bay of Bengal, eastern Vidarbha receives good rainfall in July, August and September [2].

As stated earlier the rainfall received during monsoon season is useful for the rainfed agriculture, while excess rainfall that is stored under ground or over ground is utilized for irrigating the crops during non monsoon seasons i.e. winter and summer. The knowledge of rainfall over future periods is thus useful for planning the rainfed agriculture and managing the irrigated agriculture properly. Over the last few decades, several models have been developed, attempting forecasting of rainfall. Though some of these models show notable accuracies in short term rainfall occurrence prediction [3, 4] while there are still gaps particularly when there is large temporal variations in rainfall.

Medium-to-long-term rainfall forecasting at weekly, monthly, seasonal, or even annual time scales is particularly useful in reservoir operations, irrigation management, institutional and legal aspects of water resources management and planning and rainfed agriculture. Long sequences of rainfall data are also an essential component for better decision on proper planning and management of soil conservation projects to avoid risk of either under designing or uneconomic cost of over designing at particular site. Several mathematical models based on stochastic process are available such as regression model, time series model and probabilistic models to generate and forecast the annual rainfall- runoff values. Stochastic linear models are fitted to hydrological data or time series such as temperature, humidity, rainfall, evaporation etc for two main reasons: to enable forecasts of the data one or more time periods ahead and to enable the generation of sequences of synthetic data.

The multiplicative seasonal autoregressive integrated moving average (ARIMA) have been used for generation and forecast of weekly, fortnightly and monthly values [5] for different hydrological variable in past. The ARIMA process is a powerful time series modeling and forecasting technique which possesses flexibility for the inclusion of many time series characteristic. In past ARIMA models have been used successfully to hydrological time series model [6]. Therefore, in this study it is proposed to investigate the suitability of ARIMA class of model for generation and forecasting of weekly rainfall.

MATERIAL AND METHODS

A. Study Area

The Ahmednagar district is situated in Western part of the Maharashtra. The district covers an area of 17,413 sq.km. Administratively district is divided into fourteen taluks, Rahuri is one of them which falls between 19°23' North latitude and 74° 42’ East longitude. The average annual rainfall in the district is 501.8 mm. Though heavy near the Sahyadris in Akola & plentiful in the hilly parts of Sangamner, for Rahuri, Shevgaon and Jamkhed, the rainfall is uncertain. The area chosen for this study is Rahuri where in periods of draught have been reported [7].

B. Data Acquisition

The time series data related to weekly rainfall were collected from National Data Centre of India Meteorological Department, Pune. Thirty one year’s rainfall data series (1982– 2012) of Rahuri region of Ahmednagar district were used for stochastic modeling.

C. Methodology

1 Autoregressive Integrated Moving Average (ARIMA) model

A time series involving seasonal data has relations at a specific lag ‘s’ which depends on the nature of the data, e.g. for monthly data s = 12 and weekly data s = 52. Such series can be successfully modeled only if the model includes the connections with the seasonal lag as well. Such models are known as multiplicative or seasonal ARIMA models. The general multiplicative seasonal ARIMA (p,d,q) (P,D,Q)s model has the following form.

Modelling process

Seasonal autoregressive integrated moving average are useful for modeling seasonal time series in which mean and other statistical properties for given season are not stationary across the year. The basic ARIMA model is described as a straight forward extension of the non-seasonal ARIMA models. The following modeling process [5, 9] has been used for developing the ARIMA models for weekly rainfall event.

Standardization and normalization of time series variables: The first step in time series modelling is to standardize and transform the time series. This process is required to ensure normalcy of data sequence and residuals. Many procedures are available in the literature for this purpose. In general the standardization is performed by normalizing the series as follows:

Where,

Yi,t = stationary stochastic component in the mean and variance,

Xi,t = weekly rainfall in the week t of year i,

X=weekly mean rainfall,

t = weekly standard deviation

Model identification: An important step in modeling is identification of tentative model type to be fitted to the data set. In present study the procedure stated by [8] was adopted for identifying the possible ARIMA models. A time series with seasonal variation may be considered stationary. One of the basic conditions for applying the ARIMA model on a particular time series is its stationary. A time series with seasonal variation may be considered stationary if the theoretical autocorrelation function and theoretical partial autocorrelation function are zero after a lag k = 2s + 2 (where,‘s’ is the seasonal periods, in this study, for weekly s = 52). The estimate of theoretical autocorrelation function (em) i.e. rm is obtained by equation (2). The autocorrelation functions vary between -1 and +1, with values near 1 indicating

Where,

The estimate of partial autocorrelation function (ekk) i.e mm is obtained by the equation (3). The partial autocorrelation functions vary between -1 and +1, with values near indicating stronger correlation. The partial autocorrelation function (PACF) removes the effect of shorter lag autocorrelation from the correlation estimate at longer lags.

Where,

mm= Partial autocorrelation function at lag m.

It is considered that and equal zero if

Where,

rk = Sample autocorrelation at lag k,

r Sample partial autocorrelation at lag k,

T = Number of observations

If the sample autocorrelation function (ACF) of analyzed series does not meet the above condition, the time series needs to be transformed into a stationary one using different differencing schemes. For example, (d = 0, D = 1, s = 52) according to the expression given by equation (6).

Where

yt -is stationary

d - order of non seasonal differencing operator,

D - order of seasonal differencing operator,

B - back shift operator,

s - seasonal length,

t - discrete time,

Xt -rainfall series

k - lag at period,

xt - stationary series formed by differencing series.

The time series will be stationary if the ACF and PACF cut off at lags less than k=2s + 2 seasonal periods. Thus it is necessary to test the stationary of the transformed time series obtained by differencing the original times series according to different orders of differencing (non seasonal and seasonal). The differenced series that pass the stationary series needs to be considered for further analysis. The following guidelines were used for selecting the orders of AR and MA terms [6]

If the autocorrelation function cuts off, fit ARIMA(0,d,q) x (0, 1,Q)52 model to the data, where q is the lag after which the autocorrelation function first cuts off, and Q is the lag after which seasonal ACF cuts off.

If the autocorrelation function cuts off, fit ARIMA (p,d,0) x (P,1,0)52 model to the data, where p is the lag after which the partial autocorrelation function first cuts off, and P is the lag after which seasonal PACF cuts off.

If neither the autocorrelation or partial autocorrelation functions cut off, fit the ARIMA (p,d,q) x (P,1,Q)52 model for a grid of values of p, P, and q, Q.

Thus, on the basis of information obtained from the ACF and PACF, several forms of the ARIMA model need to be identified tentatively.

Parameter estimation: After identifying model the parameters of selected model are estimated by the statistical analysis of data series. The most popular approach of parameter estimation is the method of maximum likelihood. Hence in this study, the maximum likelihood method was used for the estimation of parameters.

Diagnostic checking: Once a model has been selected and parameters calculated, the adequacy of the model has to be checked. This process is called diagnostic checking. There are number of diagnostic checking methods to test the suitability of the estimated model. These include Box-Pierce method, Portmanteau lack-of-fit test, t-statistics, standard error of the model parameters, observing ACF and PACF of the residuals, Akaike Information Criteria (AIC) and Bayes Information Criteria (BIC). However in this study following three tests will be used for the diagnostic checking of rainfall data series. Examination of standard error: A high standard error in comparison with the parameter values points out a higher uncertainty in parameter estimation which questions the stability of the model. The model is adequate if it meets the following condition.

Where,

cv= parameter value and se = standard error

ACF and PACF of residuals: If the model is adequate at describing behavior of rainfall time series, the residuals of model should not be correlated i.e. all ACF and PACF should lie within the following equation

lag k = 2s + 2

Where,

s = number of periods.

Akaike Information Criteria (AIC): AIC is computed by equation (8). The lower values of AIC are desirable

Where,

AIC = Akaike information criteria,

k = Number of model parameters,

vr = Residual variance

T = Total number of observations

Selection of the model

Root mean square error (RMSE) is used for selecting the appropriate ARIMA model amongst all the models that pass the adequacy test or diagnostic checking. In present study RMSE show how close the actual values are of rainfall with predicted values of rainfall. Lower the values of RMSE, better is the model. RMSE is estimate by equation (9).

Where,

RMSE = Root mean square error,

n = Total number of observations used for computing RMSE,

Pi and Oi are the predicted and observed values, respectively

RESULT AND DISCUSSION

To know the appropriateness of stochastic modeling of rainfall the time series were divided into the six different groups as below.

1) 1982-1986 2) 1987-1991 3) 1992-1996 4) 1997-2002 5) 2002-2006 6) 2007-2012

The statistical properties such as mean, standard deviation, skewness and kurtosis were estimated for each week of these groups. The average of weekly mean, standard deviation, skewness and kurtosis for each group were plotted and shown in fig.1. It is observed from the figure that there is no specific pattern of changes in the weekly statistical properties over different groups. Therefore, the stochastic modeling of rainfall time series was considered as the adequa

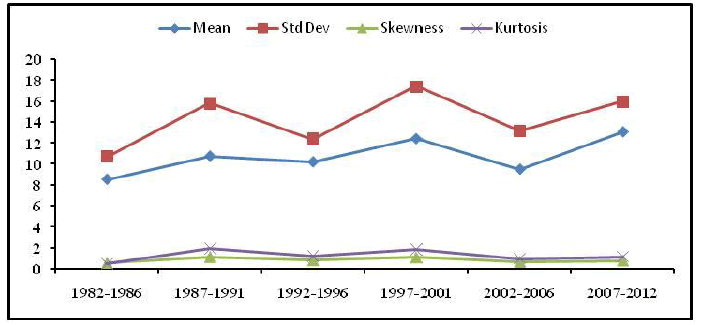Figure 1. The weekly mean standard deviation, skewness and kurtosis of rainfall of different groups of Rahuri station

Identification of model

The ACF and PACF of weekly rainfall time series were estimated for different lags. These are shown with upper and lower limits in Fig.2. It is seen from Fig.2 that ACF lies outside limits after lag k = 2s + 2 i.e. 106. Thus, ARIMA model cannot be applied the original time series of rainfall. Therefore the time series were transformed by using differencing schemes d= 1, D= 0; d=1, D=1; d=0, D=1 and d=0, D= 0. The ACF and PACF along with upper and lower limits were estimated by equation (4) and (5). It was observed that ACF of d = 1, D = 0 and d = 1, D = 1 lie within the limits of range specified by equation (4) and (5) after lag 106. Hence, these differencing schemes were used for developing ARIMA model for weekly rainfall time series.

On the basis of information obtained from ACF and PACF the orders of autoregressive (AR) and moving average (MA) terms were identified as one. Based on this several forms of ARIMA models were identified and parameters computed

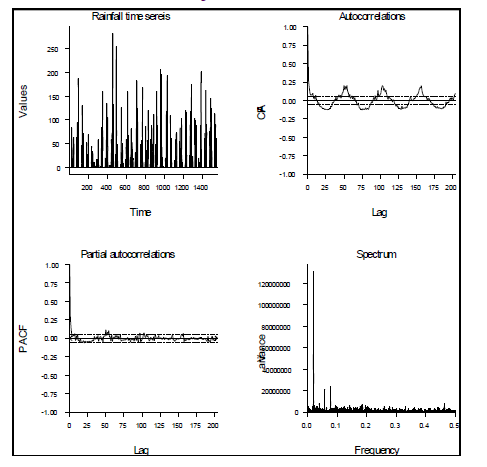Fig.2. Rainfall time series, autocorrelation and partial autocorrelation patterns of original rainfall series (d=0, D=0)

Determination of parameters and diagnostic checking

Following parameters of the selected models were calculated by maximum likelihood method.

(1) 1 (2) 1 (3) Φ1 (4) Θ1 (5). C

Out of the 36 possibilities the ARIMA models that satisfied the test for all parameters i.e. Standard error, t values and AIC values are given in Table I.

Residual of ACF and PACF

For model to be consider by adequate at all behavior of time series the residuals of model should be correlated, i.e. all ACF and PACF should lie within the limits calculated by equation (4) and (5) after lag k = 2s + 2, where, s = number of period such as s = 52 or s= 12 for this case s = 52 and the value of k = 106 computed. ACF and PACF residual series plot of several models are laid within the prescribed limits.

Selection of the best model

The eleven models with less AIC that satisfy standard error and ACF and PACF of residuals criteria were finally used for (Table II) generation of weekly rainfall values. For this purpose rainfall values were forecasted for one year with help of identified ARIMA models. These values were compared with actual values for one year by calculating the root means square error (RMSE) between them.

Based on RMSE values, ARIMA (1,1,1 ) (1,0,1 )52 model was selected for forecasting and generation of rainfall. the ACF and PACF of this model are shown in fig.3 and also the parameters of selected model are given in table III.

Comparison of forecast and actual values

The ARIMA model that were finalized to forecast the values of rainfall for Rahuri region are presented in fig. 4. These values were developed using the rainfall data from 1982 to 2011. The rainfall values were forecasted with help of best model and weekly rainfall values were calculated with help of weekly rainfall series. Forecasted values were compared with actual values of rainfall 2012.

CONCLUSION

The study indicates that the seasonal ARIMA model is available tool for forecasting the rainfall for Rahuri region of Ahmednagar district (M.S.). The system reveal that if sufficient length of data is used in model building then the frequent updating of model may not be necessary. This forecasted rainfall can be advantages management of reservoir also useful for irrigation system. ARIMA (1, 1, 1,) (1, 0, 1,)52 gave lower RMSE value (i.e. 3.11) hence, it is best stochastic model for generation and forecasting weekly rainfall values for Rahuri station. It is concluded that seasonal ARIMA model can be successfully used for forecasting.

References

Alaka Gadagil, (1986) Annual and weekly analysis of rainfall and temperature for Pune: a multiple time series approach. Inst.Indain Geographers.Vol.8.No.1. Anonymous, Water Resources. State of the environment report. Dharmaratne W.G.D. and L.D. Premarathna (2004) Development of a Rainfall forecasting model for Sri Lanka using Artificial Feed-Forward Neural Network, Proceedings of the 2nd Science Symposium-University of Ruhuna, Sri Lanka.,pp- 29-36. Perera, H.K.W.I., D.U.J. Sonnadara, and D.R., Jayewardene (2002) Forecasting the Occurrence of Rainfall in Selected Weather Stations in the Wet and Dry Zones of Sri Lanka, Sri Lankan J. Physics, 3: pp-39-53. Box,G. E. P. and G. M. Jenkins. (1976) Time series analysis, forecasting and control. Revised Edition; Holden-Day, San Francisco, California, United States Gorantiwar, S.D.(1984) Investing applicability of some operational hydrology models to West Bengal Streams. An unpublished thesis for M. Tech. (Agril. Engg) submitted to IIT, Kharagpur. Anonymous, http://ahmednagar.gov.in Hipel, K.W., Mcleod, A.I. and Lenox, W.C. (1976). Advances in Box Jenkines modeling: 1. Model construction. Water Resources Research. 13:pp- 567-575. Hipel, K.W.and A.I. Mcleod (1994) Time series modeling of water resources and environmental system, Elsevier, Amsterdam, The Netherland p.10- 13. Meshram, D. T., S.D. Gorantiwar, A.D. Kulkarni and P.A. Hangargekar (2013) Forecasting of Evaporation for Makni Reservoir in Osmanabad District of Maharashtra, India., International Journal of Advanced Technology in Civil Engineering, ISSN: 2231 –5721, Volume-2, Issue-2, pp-19-23.