ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Kaushal K. Patel1, S.J. Thanki2 P.G. Student,Department of MechanicalEngineering, Shri S‘ad Vidya Mandal Institute of Technology,Bharuch, Gujarat, India 1 Associate Professor,Department of Mechanical Engineering, Shri S‘ad Vidya Mandal Institute of Technology, Bharuch, Gujarat, India 2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
System dynamic (SD) provides a useful interpretation of business contexts, analysing how policies and decisions affect the structure of companies and the dynamics of the available resources. For this reason, it has successfully applied to many problems related to industrial management and operation research. Due to its ability to model and simulate the complex system for understanding the system behaviour over time horizon, it can be applied to Kanban production system to meet the customer demand in right quantity and time. This article presents the application of system dynamics approach in KANBAN production system. SD models for single stage single product kanban system is developed and simulated over different time horizon to study the behaviour of kanban production system. Simulation results are discussed later.
Keywords |
| System Dynamics, JIT, KANBAN System, Industrial Management |
INTRODUCTION |
| In order to remain competitive and economically successful, every organization focuses on increasing productivity, improving the quality of its products, and raising the standards of efficiency within its company. The just-in-time (JIT) management allows the organization to achieve this goal by increasing the efficiency of the production, reducing the level of wasted materials, time and effort involved in the production process. JIT philosophy recommends that a manufacturer reduce inventory by making components just in time for the subassemblies and by making the subassemblies just in time for the final assembly. Reduction in inventory is not the only goal of the JIT philosophy and it affects overall productivity in more than one beneficial way. [15] To implement the JIT philosophy, a kanban technique is introduced as an efficient operational mechanism. The improvements in reduction of inventory and wasted labor, and enhancement of customer service are usually accomplished through kanban operations. Thus, a kanban mechanism ensures the organizations to run their supply chain systems in JIT policy. In a kanban controlled system, production is triggered by the demand at the final stage. At each intermediate stage, it is triggered by its succeeding stage(s)—this process is carried all the way from the final stage to the beginning stage. Thus, the production is controlled (i.e., pulled) by demand of the succeeding stage, the customer of the preceding stage. Thus, this approach leads itself to a very simple control mechanism, best known as kanban (or pull) system. [17] Kanban controlled production systems have received much attention in the past because of the ease in which they can implement the pull control policy using a make to stock production. The production system is decomposed into several stages, each of which corresponds to a subpart of the system, where production is controlled by way of cards (called kanbans), acting as production orders. [16] |
| A. Kanban System |
| The Kanban system can be viewed as an information system that controls JIT production. Kanban is the inventory replenishment system developed by Toyota to accomplished JIT production. In Kanban production system, the production processes for various products are controlled as per the customer‘s order. Generally speaking, each item consumed, determines a replenishment signal: a production card (Kanban) is collected in a special Kanban board that displays items consumption and then used to start production or order placing according to the sequencing rules of the upstream section. There are two types of Kanbans: withdrawal kanban and production kanban. Withdrawal Kanban specifies the kind and quantity of product to be withdrawn from the subsequent process. While the production Kanban specifies the kind and quantity of product to be produced. The withdrawal Kanban is used as an inter-process signal to move physical units from one process to another process that takes place at a different location, whereas the Production Kanban is an intra-process signal to issue production orders in a particular process. As a result of this dual chain of Kanbans, the rate of production of the succeeding process is transmitted to the preceding and every process receives the necessary units at necessary time in necessary quantities. [14] A kanban usually includes the information such as part number, description, container, unit load (quantity per container), stock location (from), end process (to), and some optional information (lot size, number of kanbans per lot, machine number of final operation, individual kanban). |
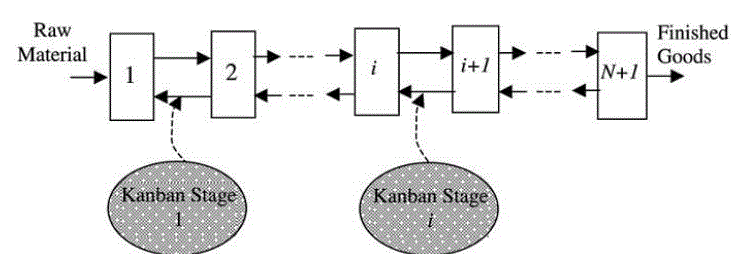 |
| Fig.1 A Multi-Stage Supply Chain System with Kanban Operations [17] |
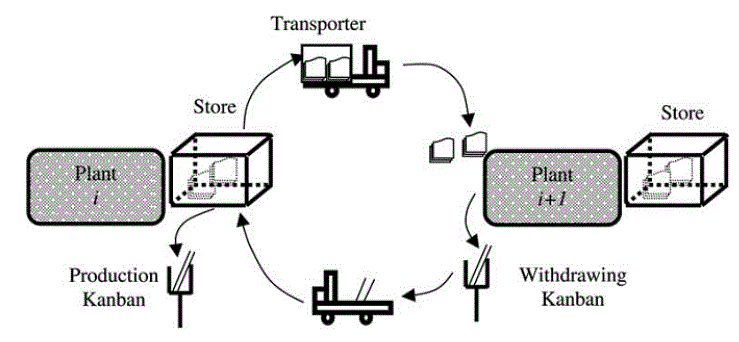 |
| Fig. 2 Operation of Kanban Production System [17] |
| The function of the kanban is best explained through the use of an N-stage production system as illustrated in Fig. 1. Two adjacent plants, i and i +1, in Fig. 1 are isolated for illustrative purpose as shown in Fig. 2. The kanban operation can be explained as, a withdrawal kanban attached to a loaded container in a succeeding plant (i+1) is detached from the container to the kanban board as the first part from the container is to be used. Then withdrawal kanbans from the kanbans board are collected and brought to the proceeding plant i at a fixed or nonfixed interval of time called kanban cycle. The withdrawal kanban is then attached to the container in a store at the preceding plant in place of the detached production-ordering kanban that triggers the production of the preceding plant to produce the required amount of parts. The containers filled with parts together with the withdrawal kanban are brought to the succeeding plant by the material handling devices called transporter. This kanban cycle realizes smooth, timely, and optimal flow of parts between preceding and succeeding plants. As the system is operated under the JIT philosophy, the stock levels in each stage should run ideally as low as possible. First, the number of kanbans in each stage should be determined; that is, the number of batches at each stage that is to be shipped by kanbans should be determined. Considering the delivering time and loading/unloading time, the number of kanbans needed to transport the batches is determined. Second, the ordering policy for the suppliers at the first stage and delivering policy for the retailers at the last stage are to be decided as well. Next, all stages should be linked together to balance the material flow in the supply pipeline. All these apparently discrete problems should be solved collectively based to minimize the total operational cost. Finally, the kanban operations at each stage should be scheduled. [17] |
| B. Implementation of System Dynamics in Kanban Production System |
| System dynamics is an approach to understanding the behaviour of complex systems over time. It is a methodology and mathematical modelling technique for framing, understanding, and discussing complex issues and problems. It deals with internal feedback loops and time delays that affect the behaviour of the entire system. System dynamics was developed by Jay W. Forrester (1950) in Massachusetts Institute of Technology (MIT). This framework is focused on systems thinking, but takes the additional some steps of constructing and testing a computer simulation model. System dynamics simulation is performed to learn about the dynamics of the system behaviour that may impact the planning solution by using closed-loop feedback and to design policies to improve system performance. It treats the interactions among the flows of information, money, orders, materials, personnel, and capital equipment in a company, an industry, or a national economy. The main characteristics of this method are the existence of complex system, the change of system behaviour from time to time and also the existence of the closed loop feedback. This feedback describes the new information about the system condition that will yield the next decision. [10] In industrial management (IM), the actual socio-economic dynamics, the aggressive competition on a global scale, more educated and demanding customers and a rapid pace of change in process technology, lead companies to frequent revision of their organizational structure, strategic objectives and decision making processes. This essentially means that companies have to show great ability in adapting to changes imposed by their own target market. Organizations need, therefore, some methods that can provide for an innovative approach to their investigations to business problems in order to identify the main cause-effect relations which characterize the environment in which they operate and find new approaches allowing for better control on production systems and more effective use of the enterprise resources. In this regard, system dynamics (SD) provides a useful interpretation of business contexts, analysing how policies and decisions affect the structure of companies and the dynamics of the available resources. [2] Due to its ability to model and simulate the complex system for understanding the system behaviour over time horizon, SD modelling and simulation can be used for demand forecasting and decision making on order placing or production planning and control in Kanban production system to meet the customer demand in right quantity and time. It will also help in policy analysis and its effects on system behaviour. It can be further used for understanding of system behaviour in respect to unexpected circumstances such as normal response, changing no. of kanbans, a breakdown, small and large demand increase, bottlenecks and capacity planning and point out some of the managerial trade-offs involved in kanban production. |
II. LITERATURE REVIEW |
| Table 1 includes the review of articles on system dynamics related to Industrial Management problems and kanban system. |
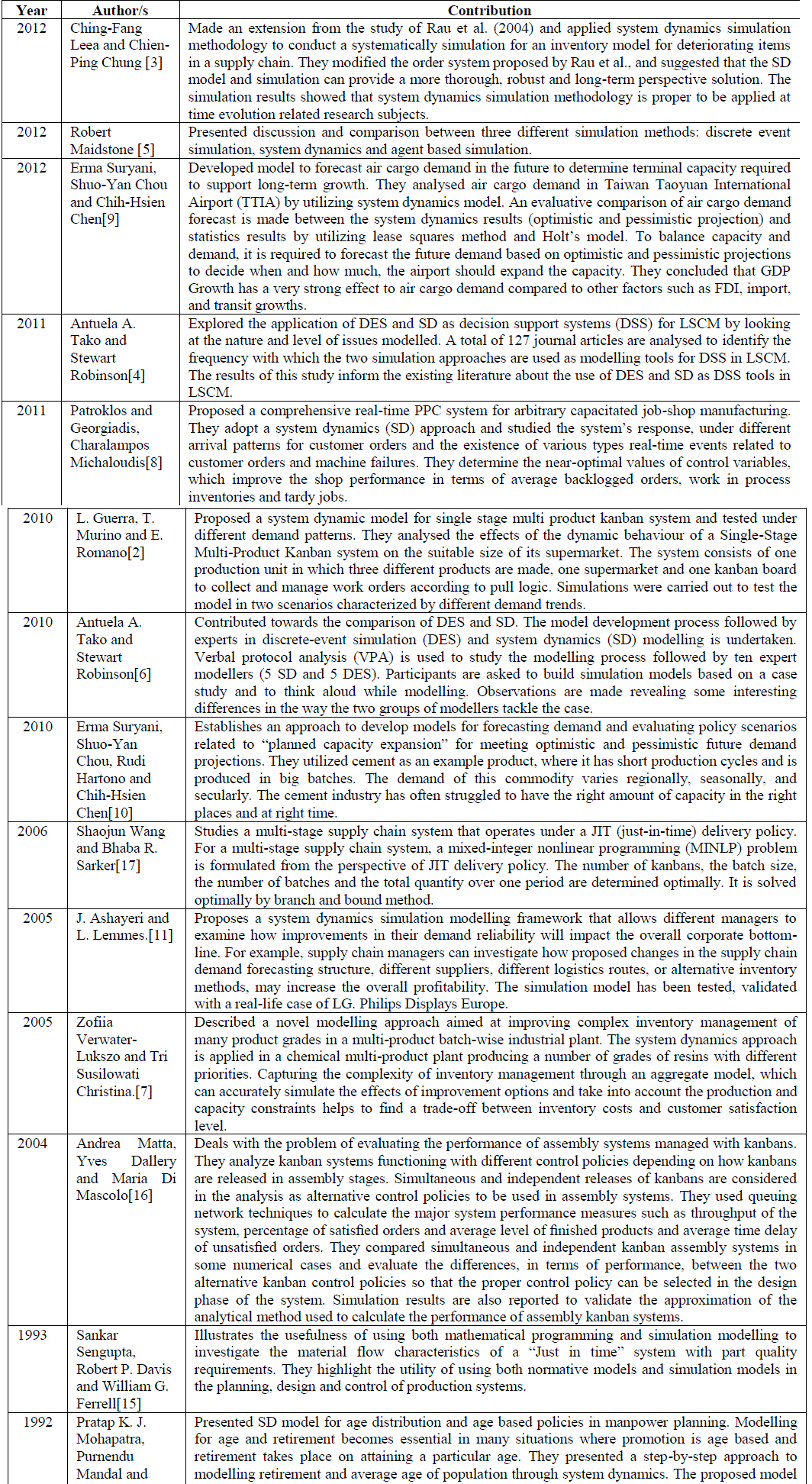 |
| Table 1-Review of Related Articles |
III. SD MODELLING OF KANBAN SYSTEM |
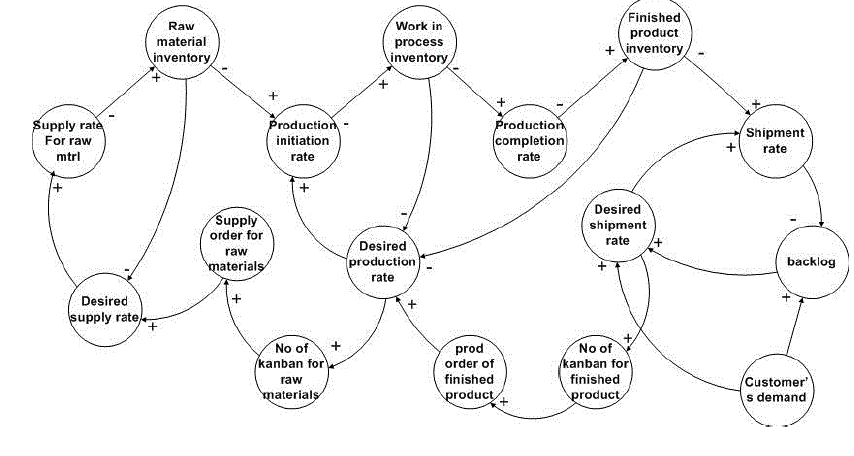 |
| Fig. 3 Causal Loop Diagram for Single Stage Single Product Kanban System |
| Fig. 3 shows causal loop diagram for single stage single product kanban system. It is created by connecting various stocks, flows and other parameters which affect the system structure and behaviour by arrows denoting the causal influences among them. This causal loop diagram shows cause and effect relations between all the variables. Each arrow represents a cause and effect relationship between two variables. The âÃâ¬Ãâ+‘ and âÃâ¬Ãâ−‘ signs represent the direction of causality. A âÃâ¬Ãâ+‘ sign indicates that if the cause increases, the effect increases; whereas the âÃâ¬Ãâ−‘ sign refers to the effect decreases as the cause increases. Casual loop diagram represents a closed loop of cause-effect linkages that intends to capture how system variables interrelate. However, link polarities only describe the structure of the system but not the behaviour of the variables. |
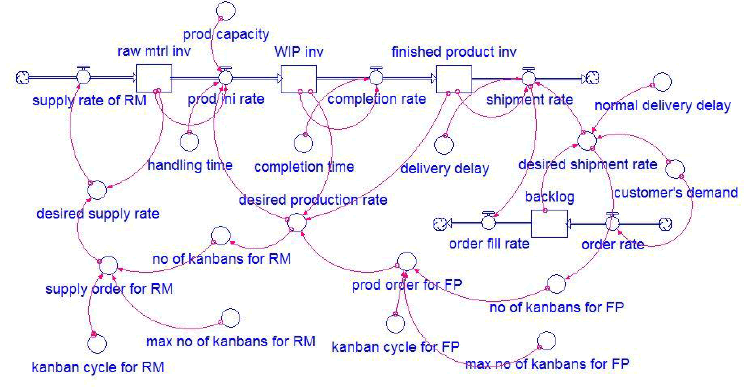 |
| Fig.4 System Dynamic Model of Single Stage Single Product Kanban System |
| We have generated simple SD model for kanban system from this causal loop diagram using STELLA software. Fig. 4 shows the basic SD model for single stage single product kanban system. It is also called stock and flow diagram (SFD). Stock and flow diagram provides the storage element of the manufacturing systems that is accumulating or draining over certain amount of time. The storage element, like stock or level, is the memory of a system and is only affected by flows. The stock is an accumulation of any particular manufacturing stage. It represents the accumulated difference between inflow and outflow rates, illustrating the results of dynamics within the system over time. Stocks are conserved quantities that can be changed only moving contents in and out. Here, supply rate for raw material, production initiation rate, completion rate and shipment rate are the flow rates and affect various inventory levels. Desired supply rate, desired production rate and desired shipment rate are the parameters which control the supply rate, production initiation rate and shipment rate respectively. Production initiation rate, completion rate and shipment rate also depends upon inventories of raw material, work in process and finished product respectively and time delays like handling time, completion time and delivery delay respectively. Production initiation rate is further limited by production capacity of the production unit or machining centre. Raw material inventory represents the accumulated difference between supply rate and production initiation rate during a certain handling time. Same way, work in process inventory represents the accumulated difference between production initiation rate and completion rate over a completion time and finished product inventory represents the accumulated difference between completion rate and shipment rate over a delivery delay. They illustrate the results of dynamics within the system over time. Another level is provided in the present model represents the backlog that is accumulated difference between order rate and order fill rate. Here, order rate is equals to customer‘s demand and order fill rate is equals to shipment rate of finished goods. Kanbans for finished product and raw material are detached depending on desired production rate and desired supply rate. No of kanbans for finished product and raw material represents the kanban board. They define the inventory allowed in the entire system. Kanbans may be withdrawal kanban or production kanban. Max no of kanbans for finished product and raw material are the upper limits for kanban board. Here, detached kanbans from kanban boards for finished product and raw material are converted into production order of finished product and supply order of raw material respectively depending on type of kanbans at regular interval of time that is kanban cycle time for both finished product and raw materials. Kanban cycle determines how fast the system reacts to changes in production rate. Handling time, completion time and delivery delay are time delays. Normal delivery delay is the sum of all these time delay associated with supply chain. It affects the desired shipment rate. Desired shipment rate is defined by sum of the customer‘s demand and backlog multiplied by normal delivery delay. The time delays make corrective actions to continue even after the state of the system reaches its goal, forcing the system to adjust too much, and triggering a new correction in the opposite direction. The most fundamental modes of system dynamic behaviour are defined as exponential growth, goal seeking, and oscillation. Each of these modes is caused by a simple feedback structure: positive feedback loop yields exponential growth, goal seeking arises from negative feedback, and negative feedback loops with time delays give system oscillation. More complex modes such as S-shaped growth and overshoot and collapse arise from the nonlinear interaction of these fundamental feedback structures. Exponential growth arises from positive feedback. The larger the quantity, the greater its net increases, further boosting the quantity and guiding even faster growth whereas, a negative loops seek balance and equilibrium. Negative feedback loops act to bring the state of the system in line with a goal or desired state. Like goal-seeking behaviour, oscillations are also caused by negative feedback loops. The state of the system is compared to its goal, and corrective actions are taken to eliminate any discrepancies. In an oscillatory system, the state of the system constantly overshoots its goal or equilibrium state, reverses, and then undershoots, and so on. The overshooting proceeds from the presence of significant time delays in the negative loop. The time delays make corrective actions to continue even after the state of the system reaches its goal, forcing the system to adjust too much, and triggering a new correction in the opposite direction. In contrast, S-shaped growth begins with an exponential growth at first, and then it gradually slows until the state of the system reaches an equilibrium level. |
IV. SIMULATION RESULTS AND DISCUSSION |
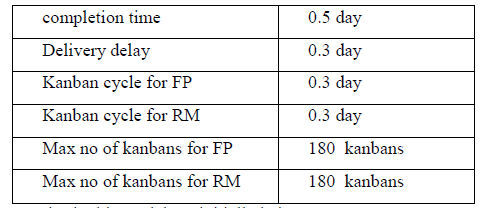
| The simulation process is carried out using STELLA 9.0 to understand the system behaviour over different time horizon. It enables us to change the input variables in SD model to study its effects on system behaviour so that we can optimize some critical parameters to solve problems involved in SD model and improve the system performance. We can also change the system policies for each parameter or flows for each runs so that we can get the best policies that appropriate for the present issues. Thus it can be helpful in policy analysis. In this model production capacity, max no of kanbans and kanban cycles for both finished product and inventory are the parameters which controls the whole production system. We can optimize these parameters by changing them and simulate each time to study the effects on system behaviour and performance. We arbitrarily choose the following system parameter values for the single stage single product kanban system model from Fig.4: |
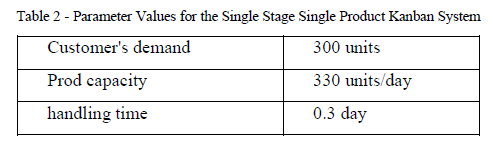 |
 |
| It is assumed that all the inventories in this model are initially being zero. The simulation carried out in STELLA 9.0 gives the results in graphical form and tabular form with respect to time duration for which SD model has run (simulated). Following figures show the simulation results for single stage single product kanban system in graphical form. |
 |
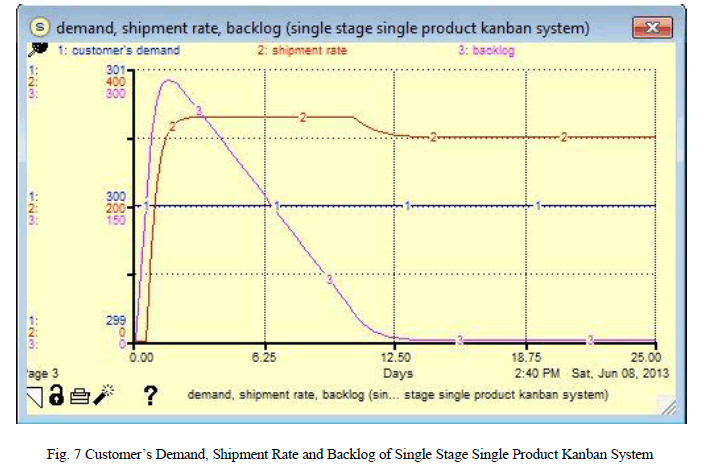 |
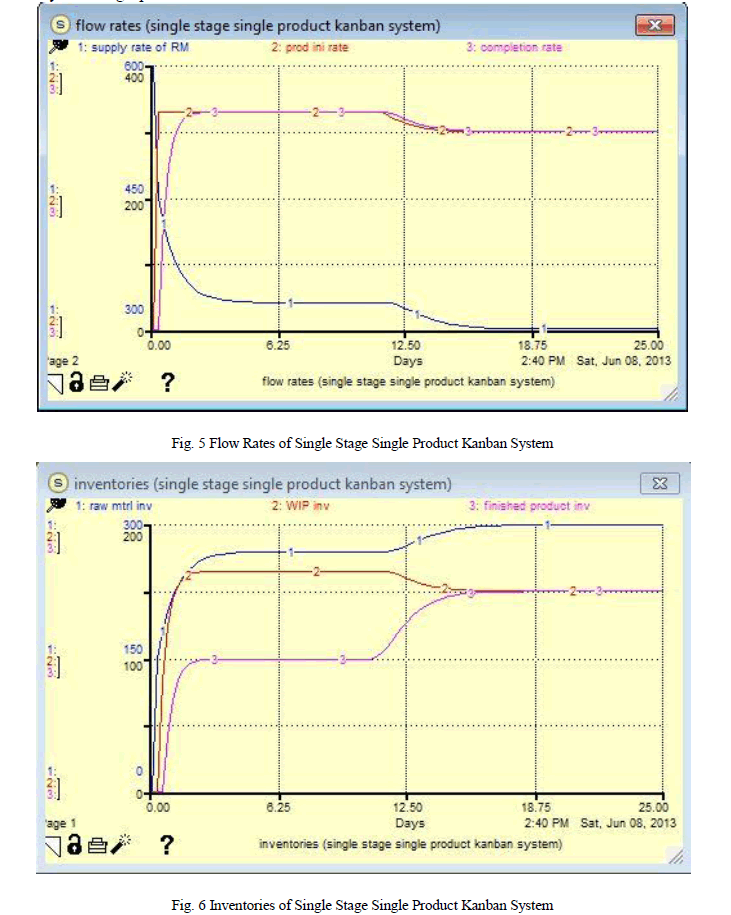
| The system dynamics model has run for 25 days. The system behaves similar to a goal seeking feedback loop structure. Fig. 5 shows the behaviour of supply rate of raw material, production initiation rate and completion rate over time. Fig, 6 shows the behaviour of raw material inventory, work in process inventory and finished product inventory over time. Similarly fig. 7 shows the behaviour of customer‘s demand, shipment rate and backlog over time. Here, we have chosen the short time period of kanban cycle as 0.3 day for both finished product and raw material so that the kanbans for production and supply are detached quickly to start the production. So the supply rate for raw material is initially at peak value to initiate the production. It will increase the raw material. As the raw material is available, the production starts and production initiation rate increases quickly from 0 to 330unit/day. This will increase work in process inventory that defines the incomplete product inventory which is under process Here, note that we have selected the production capacity as 330unit/day. It means production is carried out on max capacity of a production unit to compensate for the backlog. Here, backlog is increased rapidly as there is no finished product to deliver. Now, as the production completes, it will increase the finished product inventory. This will increase the shipment rate from 0 to 330unit/day. This will decrease the backlog level. Backlog remains zero after 14 day as it has compensated by producing parts at max capacity. The production is carried out at production capacity (330 unit/day) over first 10.5 days and then decreased from 330 to 300 unit/day. The completion rate and shipment rate behaves similar to the production initiation rate as shown in fig. 5 and 7. Raw material inventory, work in process inventory and finished product inventory shows the inventory level over time. We can see that all inventories rises initially from zero for few days as the kanbans for raw material and finished product are detached. Then, it remains constant as the production continues at max capacity. As the backlog is compensated, production rate of machining centre decreases to market demand (300units/day). This increases the raw material inventory and finished product inventory to some extent and then it remains constant. Meanwhile, work in process inventories is decrease to some extent as the production is completed. The system behaves similar to a goal seeking feedback loop structure. Here, the goal was to deliver 300 units of finished goods per day to meet the market demand. The production is achieved and controlled through kanban system. |
V. CONCLUSIONS AND FUTURE WORK |
| SD has been applied to a wide range of problems. In industrial management (IM), it is necessary to analyse, evaluate and modify the strategy and policy issues and have to make decision frequently due to dynamic environment of the market. SD has been widely used to understand the system structure and its behaviour over different time span and to spot the difficulties within the system.SD has been successfully applied to any industrial management problems like inventory management, logistic and supply chain management, production planning and control, demand forecasting and capacity expansion, human resource management, etc. In the present study, system dynamics is applied to analyse and simulate the dynamic behaviour of a Pull Kanban production system to understand and prediction of system behaviour and to point out the difficulties associated within the system structure or system policies. This paper helps to understand how kanban production system works and controls the whole production process. It can be also helpful to analyse system strategies and policies. SD model of kanban system could be simulated under different circumstances to find out difficulties in certain situations. It could be used to find out the effects of various parameters on system behaviour by changing the input parameter and for optimization of these parameters. |
References |
|