The Edge Version of Geometric Arithmetic Index of Arbitrary Subdivisions of a Wheel

Abstract

Topological indices are numerical parameters of a graph which characterize its topology and are usually graph invariant. In QSAR/QSPR study, physicochemical properties, and topological indices such as Randic, atom-bond connectivity (ABC) and edge version of geometric-arithmetic (GA) index are used to predict the bioactivity of different chemical compounds. A considerable use of graph theory has been used in this area of research. In this paper, we study the degree based molecular topological index the edge version of GA for certain subdivision of wheel graphs. We derive the analytical closed formulae for these classes of structures.

Keywords

Geometric arithmetic index, Subdivision of graph, Molecular wheel-like structures

Introduction

A single number that can be used to characterize some property of the graph of a molecule is called a topological index for that graph. There are numerous topological descriptors that have found some applications in theoretical chemistry, especially in QSPR/QSAR research [1]. The oldest topological index which introduced by Harold Wiener in 1947 is ordinary (vertex) version of Wiener index [2] which is the sum of all distances between vertices of a graph. Also, the edge version of Wiener index which was based on the distance between edges introduced by Iranmanesh et al. in 2008 [3]. One of the most important topological indices is the well-known branching index introduced by Randic [4] which is defined as the sum of certain bond contributions calculated from the vertex degree of the hydrogen-suppressed molecular graphs. Motivated by the definition of Randic connectivity index based on the end-vertex degrees of edges in a connected graph G with the vertex set V (G) and the edge set E (G) [5,6]. Vukicevic and Furtula [7] proposed a topological index named the geometric-arithmetic index (simply GA) as

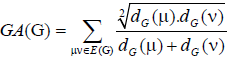(1)

where d_G(μ) denotes the degree of the vertex μ in G. The reader can find more information about the geometric arithmetic index in [7-12]. In the study carried out by Mahmiani et al. [13], the edge version of the geometric-arithmetic index was introduced based on the end-vertex degrees of edges in a line graph of G which is a graph such that each vertex of L(G) represents an edge of G; and two vertices of L(G) are adjacent if and only if their corresponding edges share a common endpoint in G, as follows

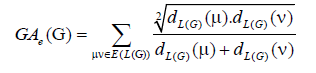(2)

where d_L(G)(μ) denotes the degrees of an edge μ of the line graph of G.

The edge version of GA index of the benzenoid graph was studied by Farahaini [14]. The total version of GA index was considered in [15,16]. Carbon nanotubes form an interesting class of carbon nanomaterials. There are three types of nanotubes: armchair, chiral, and zigzag structures. Carbon nanotubes show remarkable mechanical properties. Experimental studies have shown that they belong to the stiffest and elastic known materials. Diudea was the first chemist who considered the problem of computing topological indices of nanostructures [17-20].

A graph can be recognized by a numeric number, a polynomial, a drawing, a sequence of numbers or a matrix. A topological index is a numeric quantity associated with a graph which characterizes the topology of the graph and is invariant under graph automorphism. There are some major classes of topological indices such as distance based topological indices, degree based topological indices and counting related polynomials and indices of graphs. Among these classes degree based topological indices are of great importance and play a vital role in chemical graph theory and particularly in chemistry. The more precise way, a topological index Top (G) of a graph, is a number with the property that for every graph H isomorphic to G, we have Top (H) = Top (G). The concept of topological indices came from the work done by Wiener while he was working on boiling point of paraffin, named this index as path number. Later, the path number was renamed as Wiener index and the whole theory of topological indices started. In this paper, we have investigated the new version of geometric arithmetic index of arbitrary subdivisions of a molecular wheel graph of order n.

Definition 1. Let e be an edge with end points {μ,v} of a graph G. Subdividing the edge e means that a new vertex w is added to V(G) and the edge e is replaced in E(G) by an edge e′ with end points {μ,w} and an edge e" with end points {w,v}.

Definition 2. Subdividing a graph G means performing a sequence of edge-subdivision operations. The resulting graph is called a subdivision of the graph G. A subdivision of a graph is a graph formed by subdividing its edges into paths of one or more edges.

Example 1. Performing any k-subdivisions on the n-cycle graph C_n yields the (n+k)-cycle graph C_n+K.

Definition 3. The barycentric subdivision of a graph G is the subdivision in which one vertex is inserted in the interior of each edge.

Main Results and Discussion

In this section, we first give the edge version of GA index of some standard graphs and then the main results of this paper will be given.

Example 2. Let P_n be a path with n vertices. Then, the edge version of the geometric arithmetic index of P_nn is GAe(P_n)=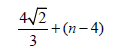

Example 3. Let S_n be a star graph with n vertices. Then, the edge version of the geometric arithmetic index of S_n is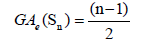

Example 4. Let K_n be a complete graph with n vertices. Then, the edge version of the geometric arithmetic index of complete graph, K_n is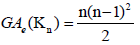

Example 5. Let C_n be a cycle with n vertices. Then, the edge version of geometric arithmetic index of C_n is GAe(K_n)=n.

Example 6. Let W_n be the wheel graph with n vertices. Then, the edge version of geometric arithmetic index of W_n is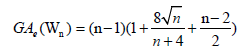

Subdivision of the Cycle of the Wheel Graph W_n

In this subsection, we will give the edge version of the subdivision of a wheel graph with respect to the subdivision on the cyclic edges only. Firstly, we consider the following example.

Example 7. Let W_5,1 be the graph obtained by the barycentric subdivision of the cycle of the wheel of order 5 as depicted in Figure 1. It is easy to see that the line graph of W_5,1 has 22 edges. On the hand, there are 8 edges with d_L(G)(μ)=d_L(G))(v)=3, 8 edges of type d_L(G)(μ)=3, d_L(G)(v)=5, and 6 edges with d_L(G)(μ)=d_L(G)(v)=5.

The edge version of geometric arithmetic index of W_5,1 is given as: G_Ae (W_5,1 ) =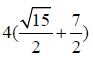

Lemma 1. Let W_n be the wheel graph with n vertices and W_n,1 is the graph obtained after the barycentric subdivision of the cycle of the wheel. Then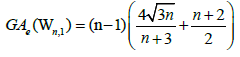

Proof. It is easy to see that the line graph of W_n,1 has 4(n-1) +|K_n-1| edges. On the hand, there are 2(n – 1) edges with d_L(G) (μ)=d_L(G)(v)=3, 2(n-1) edges of type d_L(G)(μ)=3,d_L(G)(v)=n, and |K_n-1| edges with d_L(G)(μ)=d_L(G)(v)=n.

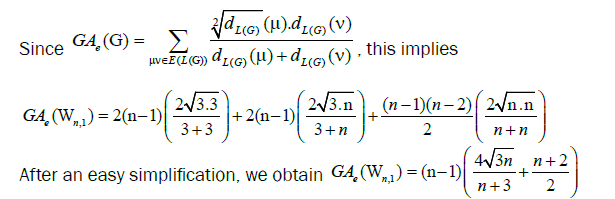
Lemma 2. Let W_n be the wheel graph with n vertices and W_n,2 is the graph obtained after the barycentric subdivision of the cycle of the wheel. Then, the edge version of geometric arithmetic index of W_n,21 is given as: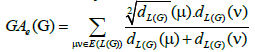

Proof. The line graph of W_n,2 has 5(n - 1) +|K_n-1| edges. On the hand, there are 2(n - 1) edges of type d_L(G)(μ)=2, dL(G) (v)=3, (n–1) edges with d_L(G)(μ)=d_L(G)(v)=3, 2(n - 1) edges of type d_L(G)(μ)=3, d_L(G)(v)=n, and |K_n-1| edges with d_L(G)(μ)=d_L(G)(v)=n.

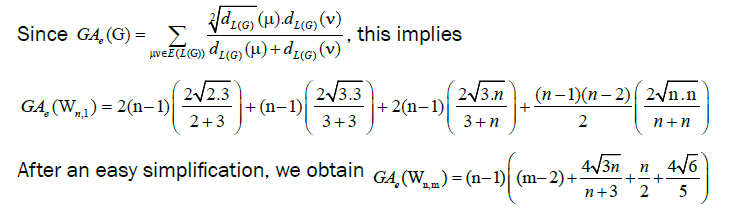
Example 8. Let W_5,3 be the graph obtained by the uniform 3-subdivision of the cycle of the wheel of order 5. Then

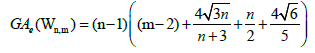
Lemma 3. Let W_n be the wheel graph with n vertices and W_n,m is obtained after the uniform m-subdivision of the cycle of the wheel by m vertices. Then, the edge version of geometric arithmetic index of W_n,m is given as:

Proof. The line graph of W_n,2 has (m+3)(n-1)+|K_n-1| edges. On the hand, there are (m-2)(n-1) edges of type d_L(G)(μ)=d_L(G)(v)=2, 2(n-1) edges of type d_L(G)(μ)=2, d_L(G)(v)=3, (n-1) edges with d_L(G)(μ)=d_L(G)(v)=3, 2(n-1) edges of type d_L(G)(μ)=3, d_L(G)(v)=n, and |K_n-1| edges with d_L(G)(μ)=d_L(G)(v)=n.

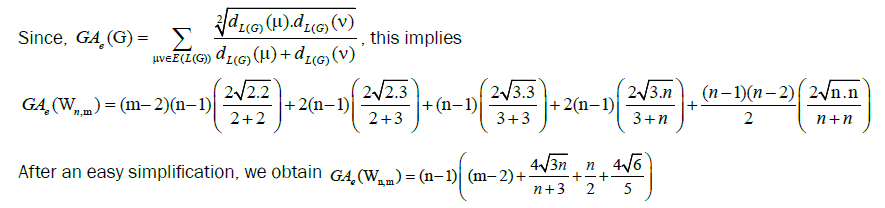
Example 9. Let W_5,2,3,4,5 be the graph obtained by the subdivision of the cycle of the wheel of order 5. Then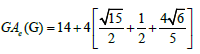

Theorem 1. Let W_n be the wheel graph with n vertices and the graph G=W_{n,k1,k2,k3,…,kn-1} is obtained by sub diving the edges of cycle of the wheel by k₁,k₂,k₃,…,k_n-1 vertices, where k_i ≥ 3 for each i=1,2,3,…,n-1. Then, the edge version of geometric arithmetic index of the graph G is given as:

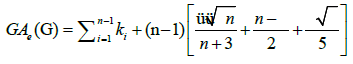
Proof. Since the line graph of a path P_ki of length k_ia path of length k_i-1so the line graph of W_{n k1,k2,k3,…,kn-1} has edges. On the hand, there are edges of type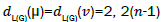 edges of type d_L(G) (μ)=2, d_L(G)(v) = 3,

(n - 1) edges with d_L(G) (μ)= d_L(G)(v) = 3,2 (n - 1) edges of type d_L(G) (μ)=3 , d_L(G)(v) = n and |K_n-1| edges with d_L(G) (μ) = d_L(G) (v) = n

Since, 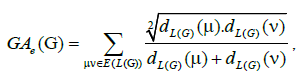this implies

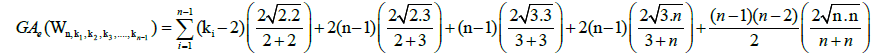
After an easy simplification, we obtain

Let G=W_{n,k1,k2,k3,…,kn-1} be a graph obtained from the subdivision of the edges of the cycle of a wheel graph W_n of order n, where,

k_i = 1, for each i=1,2,3,....,t and k_i ≥ 2 for each i = t+1,t+2,....,n-1.

In fact, we can relabelled the number of edges on the cycle of the wheel so that, so that we get the desired label of the subdivision. The edge partitions of the graph G are as follows:

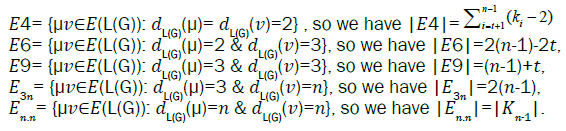
Example 10. Let W_5,1,1,2,3 be the graph obtained by the subdivision of the cycle of the wheel of order 5 as depicted in Figure 2. Then, the edge version of geometric arithmetic index of W_5,1,1,2,3 is given as:

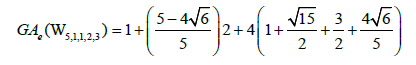
Theorem 2. Let W_{n,k1,k2,k3,…,kn-1} be a graph obtained from the subdivision of a wheel graph of order n, where, k_i = 1 for each i=1,2,3,....,t and k_i ≥ 2 for each i = t+1,t+2,....,n-1.Then, the edge version of geometric arithmetic index of W_{n,k1,k2,k3,…,kn-1} is given as:

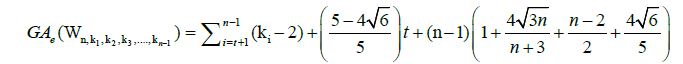
Proof. From Equation 2, we have

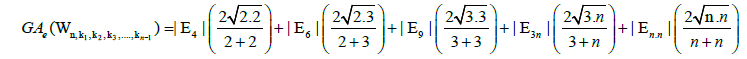
Using the cardinalities of the edge partitions and after simplifications, we get

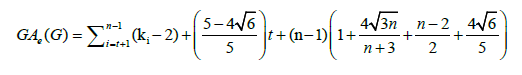
Subdivision of the Spoke of the Wheel Graph W_n

In this subsection, we will give the edge version of the subdivision of a wheel graph with respect to the subdivision on the spoke of the wheel only.

Example 11. Let (W¹₅) be the graph obtained by the barycentric subdivision of the spoke of the wheel of order 5. Then

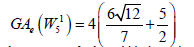
Lemma 4. Let W_n be the wheel graph with n vertices and (W²_n) is the barycentric subdivision of the spokes of the wheel. Then

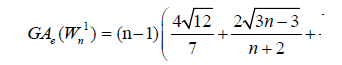
Proof. By continuing an induction argument on n, one can check that in general, the line graph of (W¹_n) has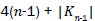 edges. On the hand, there are (n-1) edges with d_L(G) (μ)=3, d_L(G)(v) = 4 (n-1) edges of type d_L(G) (μ)=3, d_L(G)(v) = n-1 and |K_n-1| edges with d_L(G) (μ)=, d_L(G)(v) = n-1.

So, by Equation 2, we have

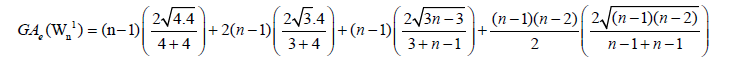
After an easy simplification, we obtain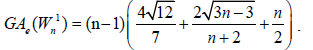

Lemma 5. Let W_n be the wheel graph with n vertices (W²_n) is the uniform 2-subdivision of the spokes of the wheel. Then, the edge version of geometric arithmetic index of (W²_n) is given by:

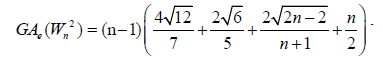
Proof. By continuing an induction argument on n, one can check that in general, the line graph of (W²_n) has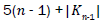 edges. On the hand, there are (n-1) edges of type d_L(G) (μ)= d_L(G)(v) = 4,2 (n-1) edges with d_L(G) (μ) = 3 & d_L(G)(v) = 4,(n-1) edges of type d_L(G) (μ) = 2 & d_L(G)(v) = 3,(n-1) edges of type d_L(G) (μ) = 2 , d_L(G)(v) = n-1 and |K_n-1| edges with d_L(G) (μ) = d_L(G)(v) = n-1.

Since, 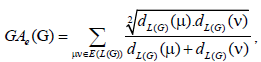this implies

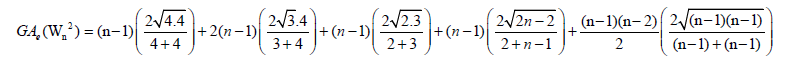
After an easy simplification, we obtain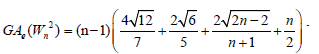

Theorem 3. Let W_n be the wheel graph with n vertices W^m_n is the uniform m -subdivision of the spokes of the wheel by m>2 vertices. Then, the edge version of geometric arithmetic index of W^m_n is given as:

Proof. It is easy to see that the line graph of Wnm has 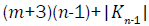edges. On the hand, there ar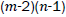e edges of type d_L(G) (μ) = 2 , d_L(G)(v) = n-1 edges of type d_L(G) (μ) = 2 , d_L(G)(v) = 3 ,(n-1) edges of type d_L(G) (μ) = 3 , d_L(G)(v) = 4 ,(n-1) edges of type

d_L(G) (μ) = d_L(G)(v) = 4 , 2(n-1) edges of type d_L(G) (μ) = 2 , d_L(G)(v) = n-1 and |K_n-1| edges with d_L(G) (μ) = d_L(G)(v) = n-1.

Since, 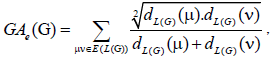this implies

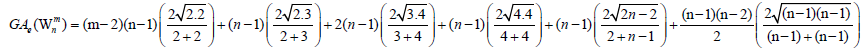
After simplification, we obtain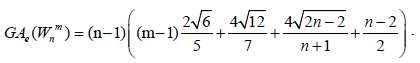

Arbitrary Subdivision of Wheel Graph

In this subsection, we will give the edge version of the arbitrary subdivision of a wheel graph.

Lemma 6. Let W_n be the wheel graph with n vertices and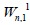 is the barycentric subdivision of the wheel graph Then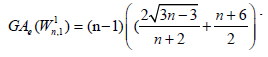

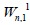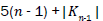Proof. By continuing an induction argument on n one can check that in general, the line graph of has edges. On the hand, there are 4 (n-1) edges with d_L(G) (μ) = d_L(G)(v) = 3 ,(n-1) edges of type d_L(G) (μ) = 3 , d_L(G)(v) = n-1 and |K_n-1| with d_L(G) (μ) = d_L(G)(v) = n-1

Since, 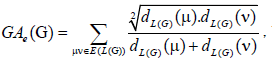this implies

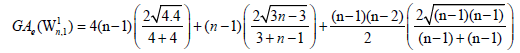
After an easy simplification, we obtain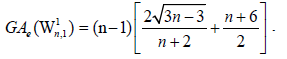

Lemma 7. Let W_n be the wheel graph with n vertices and 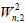is the 2-uniform subdivision of the wheel graph. Then

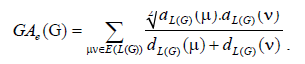
Proof. By continuing an induction argument on n, one can check that in general, the line graph of W_n has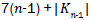 edges. On the hand, there are 3 (n-1) edges with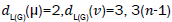 edges of type 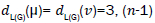edges of type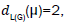 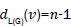and |K_n-1| edges with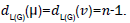

Since, 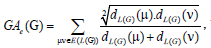this implies

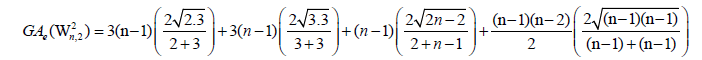
After an easy simplification, we obtain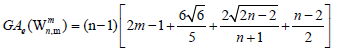

Theorem 4. Let W_n be the wheel graph with n vertices and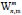 is the uniform m>2 -subdivision of the wheel. Then, the edge version of geometric arithmetic index of 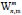is given as

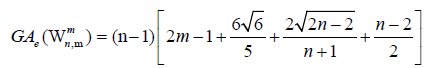
Proof. By continuing an induction argument on n, one can check that in general, the line graph of Wn has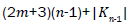 edges. On the hand, there ar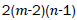e 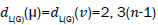edges of type 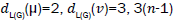edges of type edges of type 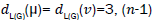edges of type 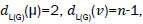and |K_n-1| edges with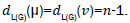

Since, 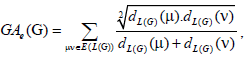this implies

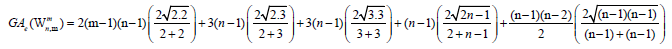
After an easy simplification, we obtain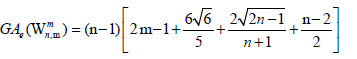

Let 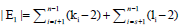be a graph obtained from the subdivision of the edges of the wheel graph W_n of order n, where, k_i=1, for each 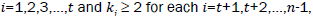for the edges of cycle of the wheel and l_i=1 for each i = 1,2,3,..., s and l_i≥ 2 for each 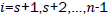for the spokes of the wheel.

The edge partitions of the graph G are as follows:

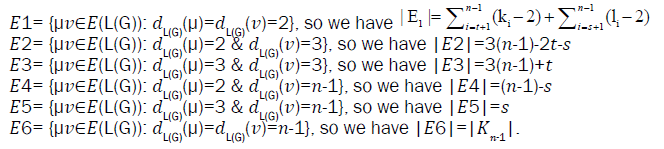
Example 12. Let 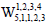be the graph obtained by the subdivision of the wheel of order 5 as depicted in Figure 3. Then

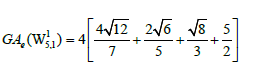
Theorem 5. Let 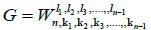be a graph obtained from the subdivision of a wheel graph. Then, the edge version of geometric arithmetic index of G is given as: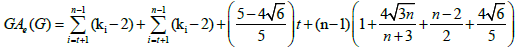

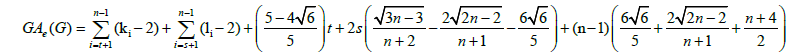
Using the cardinalities of the edge partitions and after simplifications, we get

Conclusion

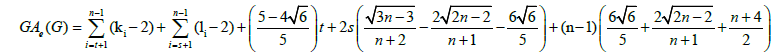
In Theoretical Chemistry, the topological indices and molecular structure descriptors are used for modeling physicochemical, toxicological, biological, and other properties of chemical compounds. In recent years, some researchers are interested in studying the topological indices of certain nanotubes and nanotori, for example, see [21,22]. In this paper, we have investigated the new version of the geometric arithmetic index of arbitrary subdivisions of a wheel graph of order n.

Acknowledgements

This research is partially supported by the University Grant, University of Sharjah, Sharjah, UAE.

References

1. Todeschini R, Consonni V. Handbook of Molecular Descriptors. Wiley-VCH, Weinheim, Germany; 2000.
2. Yuan Y, et al. On geometric-arithmetic index. J Math Chem. 2010;47:833.
3. Iranmanesh A, et al. The edge versions of the Wiener index. MATCH Commun Math Comput Chem. 2009;61:663.
4. Randic M. Characterization of molecular branching. J Amer Chem Soc. 1975;97:6609.
5. Gutman I, Furtula B. Recent Results in the Theory of Randic Index. University of Kragujevac and Faculty of Science Kragujevac, Russia; 2008.
6. Li X, Gutman I. Mathematical Aspects of Randic-Type Molecular Structure Descriptors. University of Kragujevac and Faculty of Science Kragujevac, Russia; 2006.
7. Vukicevic D, Furtula B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J Math Chem. 2009;46:1369-1376.
8. Fath-Tabar GH, et al. A new geometric–arithmetic index. J Math Chem. 2010;47:477-486.
9. Ali A, et al. A note on the zeroth-order general Randic index of cacti and polyomino chains. Iranian J Math Chem. 2014;5:143-152.
10. Ali A, et al. Some vertex-degree-based topological indices of polyomino chains. J Comput Theor Nanosci. 2015;12:2101-2107.
11. Ali A, et al. Vertex-degree-based topological indices of some dendrimer nanostars. Optoelectronics Adv Materials-Rapid Commun. 2015;9:256-259.
12. Ali A, et al. Optoelectronics Adv. Materials-Rapid Commun. 2016;10:1-2.
13. Mahmiani A, et al. On the Edge Version of Geometric-Arithmetic Index. Dig J Nanomat Biostruc. 2012;7:411-414.
14. Farahaini MR. Proc Rom Acad Ser B. 2013;15:83.
15. Mahmiani A, et al. Submitted.
16. Mahmian A, Khormali O. On the edge and total GA indices of some graphs. Int J Indust Math. 2013;5:259-263.
17. Diudea MV, Graovac A. Toranes versus Torenes. Commun Math Comput Chem. 2001;44:117-133.
18. Diudea MV, John PE. Covering polyhedral tori. Commun Math Comput Chem. 2001;44:103-116.
19. Diudea MV. Graphenes from 4-Valent Tori. Bull Chem Soc Jpn. 2002;75:487-492.
20. Diudea MV, Stefu M. Math Comput Chem. 20011;44:103.
21. Asharafi AR, et al. The eccentric connectivity index of nanotubes and nanotori. J Computational Appl Maths. 2011;235:4561-4566.
22. Ghorbani M, et al. Computing GA index and ABC index of V-phenylenic Nanotube. Optoelectron. Adv Mater Rapid Comm. 2011;5:324-326.