ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Prof. P. B. Pande1, Dr. S.P. Bajad2, Dr. S. R. Khandeshwar3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The focus of the study in this paper is directed towards understanding the rate of reduction in bearing capacity after submergence is very much dependent on degree of saturation and respective c- ï¦ parameters. Also this study proposed the approach for calculating bearing capacity (qu) under submerged condition using actual values of c- ï¦ parameters by considering initial degree of saturation. The calculated values were verified (validate) with model studies by simulating field condition performed with isolated surface circular footing resting on c- ï¦ soil. The calculated values are well agreed with values obtained from model studies. In the study of model footing it is revealed that in case of degree of saturation greater than 85%, the reduction in the ultimate bearing capacity was 40% and in case of degree of saturation less than 85% the bearing capacity got reduced by 80% for the same soil
Keywords |
| Degree of saturation, ultimate bearing capacity, submergence. |
INTRODUCTION |
| The variation of moisture content stored in the ground and earth structures under varying environmental conditions is an important aspect closely related to the mechanical behaviour of partially saturated soils. Change in the degree of saturation can cause significant changes in volume, shear strength and hydraulic properties, consequently bearing capacity. Eventually the soil may get submerged and bearing capacity will get reduced. |
| The bearing capacity is the most important soil property, which governs the design of foundation. Bearing capacity and the settlement are the two important parameters in the field of geotechnical engineering. Civil engineering projects such as buildings, bridges, dams and roadways require detailed subsurface information as part of the design process. Bearing capacity is affected by various factors like change in level of water table, eccentric loads, inclined loads, dimensions of the footings, etc. |
| Water table at the site remains at great depth so as to create unsaturated state of foundation soil. In unsaturated case the ultimate bearing capacity of shallow foundation is analytically estimated by using any of the available bearing capacity equations. However the water table eventually rises up and reaches the foundation level and the soil becomes submerged. In submerged case soil foundation system exhibits reduced bearing capacity. |
| Bearing capacity of shallow foundation is often reduced during the spring thaw, partly because. The present paper concerns the effect of degree of saturation on bearing capacity which is a function of the apparent angle of internal friction and of the apparent cohesion as evaluated by direct shear tests. The apparent friction angle decreases rapidly with increasing pore pressure coefficient and the apparent cohesion increases rapidly with increasing degree of saturation and pore coefficient. Calculation of the ultimate bearing capacity of shallow foundation has done by using universally accepted Terzhaghi’s bearing capacity. The shear strength and other parameters used in the equations are taken with respect to degree of saturation. |
II. REVIEW OF LITERATURE |
| This aspect of effect of degree of saturation on reduction in the bearing capacity of shallow foundation is comparatively the most neglected aspect with respect to both analytical treatment and actual experimentation. Theoretically this aspect has been covered to a limited extent by only few investigators (Krishnamurthy, S. and Kameshwara Rao (1925), Ausilio and Conte (2005), De Simone and Zurlo (1987) Hansen et. al. 1987). Experimental investigations and observation on this aspect are still very limited (Murtaza et. Al .1995). |
| Ernesto Ausilo and Enrico Conte(2003) studied Influence of groundwater on the bearing capacity of shallow foundation by using kinematic approach of limit analysis. S.Y.Oloo and D.G.Fredlund(1997) proposed a solution which quantify the reduction in bearing capacity arising from a static water table at any depth in any kind of soil. |
| Booking and Fredlund (1980) concluded that for a degree of saturation above of 85% the air permeability was effectively zero. |
| Most of the rainfall-induced slope failures are shallow and occur at high degree of saturation (low matric suction). It has been recognized that an unsaturated soil behaves differently at wetting and drying. Therefore, studies of the effect of wetting and drying on the unsaturated residual behavior of soils under different net normal stresses are recommended. |
| The method available for calculating ultimate bearing capacity of shallow foundation under submergence of soil is different from each other. Some empirical coefficients are given to multiply to third term of Terzaghi bearing capacity equation, while calculating the ultimate bearing capacity of submerged soil. As not much practical test data is available regarding the ultimate bearing capacity of shallow foundation with respect to submergence of soil. By keeping the concept of unsaturated soil mechanics nobody consider the degree of saturation while calculating ultimate bearing capacity of shallow foundation either in unsaturated condition or in submerged condition. The present work has been undertaken to know the same basic aspects in this respect. As a first attempt in evaluating the effect degree of saturation on reduction in ultimate bearing Capacity of shallow footing foundation (qu) the following soil-foundation system is considered. |
III. BASIC CONSIDERATION IN MODEL STUDY |
| Surface circular footing placed on soil in two cases, in first case soil is under unsaturated condition (US) and in second case soil is under submerged soil condition (SUB). In order to observe any effect of footing size on qu in both US & SUB cases 3 model footing of diameter 8.66, 12.25, 15 cm were selected. Thus the diameter proportions are 1: 2: 3. The soil selected in the study is “C-φ soil”. Thus soil used in the investigation is expected to indicate the effect of cohesion and friction component on qu of surface footing foundation on C-φ soil. With these considerations, the soil used was, Garden soil i.e C-φ soil (which is mainly a mixture of silt , fine sand, clay medium sand particle),but in actual practice different types of soils are available on which foundation of building is erected. And regarding water table in actual field condition soil contains some sort of moisture. So the soil containing initial water contents was considered for laboratory investigation. To carry out the model study a loading frame was fabricated and Circular footing of three different sizes was tested in unsaturated(US) and submerged(SUB) condition on two different initial saturation of soil. |
| Following are the cases investigated in the model study. |
| 1. On soil with model footing of diameter 8.66 cm, 12.25 cm, and 15cm Submerged cases with initial degree of saturation of soil of about 90% (Sr1). |
| 2. On soil with model footing of diameter 8.66 cm, 12.25 cm, and 15cm Submerged cases with initial degree of saturation of soil of about 75% (Sr2). |
| The laboratory investigation was planned with various considerations and aspects as discussed earlier. The details of these model studies are presented in the Thesis chapter. |
| A detailed and comprehensive methodology of the scheme of laboratory investigations, test set up and testing procedures are carried out for evaluation of load settlement curve and ultimate load bearing capacity of model footing. |
ïÃâ÷ Properties of the Tested Soil |
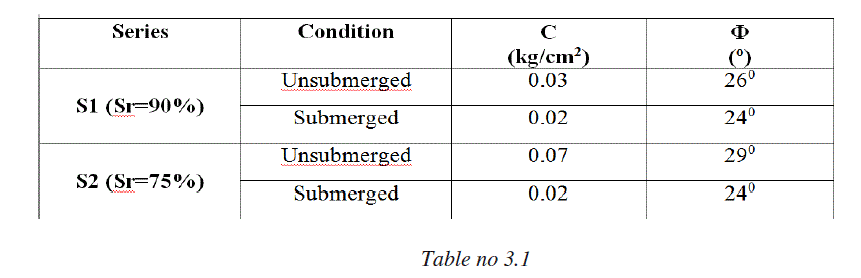
| The prepared soil sample is taken and analysed in the laboratory for determination of its various physical and engineering properties i.e. grain size distribution, shear strength parameters i.e. angle of internal of friction (φ), cohesion (c), Bulk density(γ), dry density (γd), water content (ω), degree of saturation (Sr) etc. The summary of soil properties are given in following table no 3.1 & table no 3.2: |
 |
IV. EXPERIMENTAL WORK |
| In order to carry out the investigation program in the laboratory on model footing of varying sizes, the testing tank, saturation tank, load application mechanism etc are specially developed, designed and fabricated as shown in fig. 4.1. The soil sample collected was pulverized into finer. This pulverized soil is then spread as a thin layer and allowed to air dry for sufficient time, to reduce the hygroscopic moisture to a considerable level. This prepared soil sample is then sieved through 4.75 mm IS sieve and the sieved material is collected into gunny bags for storage in dry place as processed soil sample for carrying out further investigations. |
| A perforated tank was placed in the saturation tank both the tank is kept in the Centre of test setup. The calculated quantity of processed soil is taken and thoroughly mixed. Then this soil was prepared with known degree of saturation and was kept ready to be filled in the testing tanks in layer and prepared soil sample was compacted layer by layer thoroughly and uniformly with the help of tamping hammer for conditioning the model load test. Load was applied with the help of specially designed lever arm loading arrangement. A special arrangement which is designed to measure the settlement of footing was placed in the position and two dial gauges are provided to observe the settlements when the model footing was loaded. Incremental load were put till dial gauge reading would not give constant reading. The final dial gauge readings were noted just before putting load. |
| When the test is completed dial gauges and other accessories are removed and soil sample were removed from the testing tank and another sample was filled in the testing tank, the soil sample is submerged for sufficient period of time by pouring the water into saturation tank. Then model footing is placed on top of soil bed and loading test was conducted as in the same manner explained above for submerged case. |
| The laboratory investigation involving twelve model tests for surface circular footings on C-Φ soils was carried out to study the effect of degree of saturation on reduction in the ultimate bearing capacity of footings. The study incorporated the following five variables: |
| 1. Three sizes of model footing of diameters 8.66 cm, 12.25cm & 15cm. |
| 2. Two initial degree of saturation with Sr = 90% and Sr = 75%. |
 |
V. ANALYSIS OF THE RESULTS AND DISCUSSION |
ïÃâ÷ Load-Settlement Characteristics: |
| Load settlement curve as obtained from model tests are studied. The load settlement curve for one of the model test having initial degree of saturation 90% using 12.25 diameter circular footing in unsaturated and submerged condition is as shown in Fig. 5.1 |
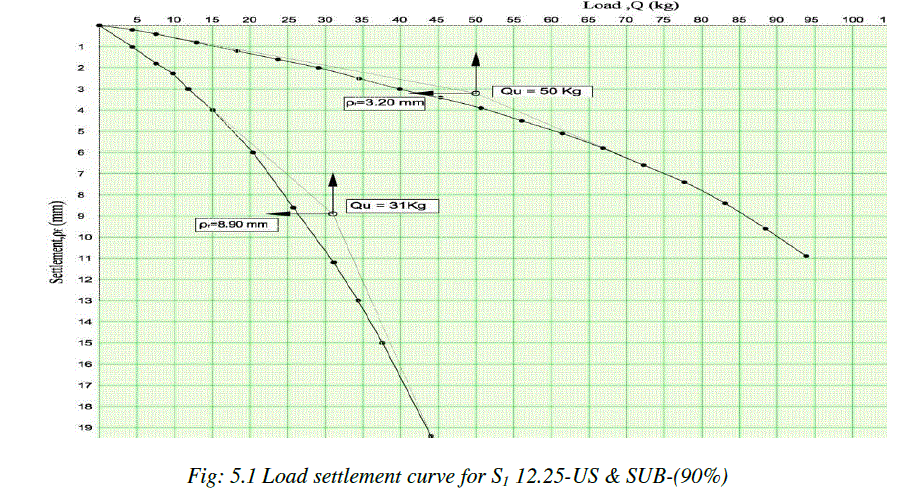 |
| The ultimate load indicating the failure state of the soil-foundation system was determined for each curve by double tangent method, considering initial portion of the curve and the later steep section of the curve as obtained in typical cases of series-1(Sr = 90%) and series – 2 (Sr = 75%) . As seen from the figures it is evident that in all the cases the load-settlement curves for full submergence of soil are much below the curves pertaining to unsaturated state of soil. The extent of difference between these two curves appears to depend, the Initial physical state of the soil (i.e. in US case) with respect to the degree of saturation and also the size of the circular model footing. |
ïÃâ÷ Theoretical computations of ultimate bearing capacity |
| There are numerous methods and theories as reported in the literature for determining the ultimate bearing capacity of shallow foundation (especially various types of footing). It is realised that most of the theories are evolved for 2D analysis pertaining to strip footing. So far as isolated footings (like rectangular, square or circular types) are concerned, in reality it is a three dimensional analysis. Practically there is no such logical three dimensional theoretical analyses for calculating the ultimate bearing capacity of shallow or surface isolated footing. In absence of this, an empirical approach of incorporating the shape factor in bearing capacity equation is commonly recommended. Here also, there appears a very wide variation in considering the value of the shape factor. Initially, Terzaghi (1943) in his classical bearing with capacity analysis recommended the shape factors Sc, Sq and Sγ in three terms of bearing capacity equation as 1.3, 1.0, and 0.6 respectively and accordingly qu for circular footing is, |
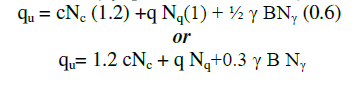 |
| Later on various investigators have suggested different values, sometimes the form of equations, for such shape factors. Considering the various approaches, the following three approaches are considered in the present study for theoretical computation of the ultimate bearing capacity of circular surface footings under unsaturated conditions: |
| 1. Terzaghi’s analysis (1948) |
| 2. Method incorporated in I.S. Code (which in fact is based is Hansen analysis (1961) and Vesic’s formulae). (1973) |
| 3. Michalowski’s method (1997) |
| In present study the approach for theoretical computation of the ultimate bearing capacity of circular surface footings under submerged condition is suggested. In suggested approach parameters should be determined by taking UD sample and tested under submerged condition. Nc and Nγ are to taken from the value of obtained under submerged condition. Also bulk density has to be worked out. Here we can say all the values required for the computation of bearing capacity should be worked out accurately under submergence |
| This feature of theoretically computed value of qu indicates that the shear strength parameters (especially Ø value of C-Ø soil) should be determined with utmost precision for accuracy of computed bearing capacity of shallow foundation. |
| It may be inferred that though there is only marginal change in the values of Nc and Nγ calculated by different approaches, the values of shape factors Sc and Sγ vary with wide difference if obtained from the three approaches / methods under consideration. This obviously affects the calculated values of qu by different methods. For comparing or characterizing the effect of submergence the factor (FSUB ) is employed. |
ïÃâ÷ Comparison of experimental values of qu with theoretical values: |
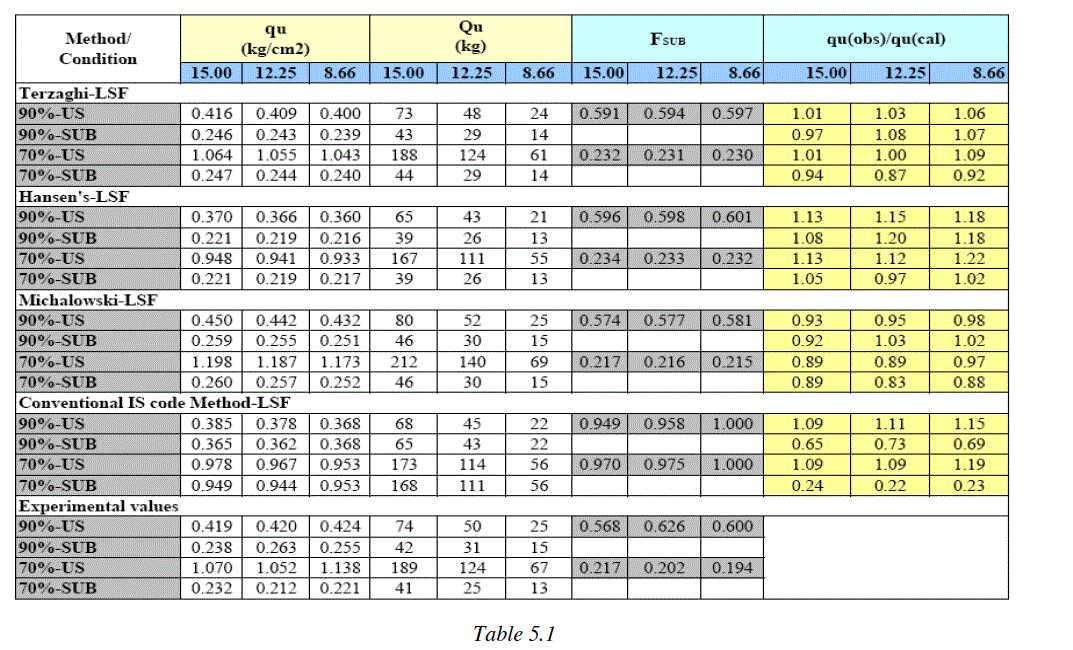
| The Table 5.1 also incorporates the experimental values of qu for all the 12 cases along with theoretical values as obtained by three different approaches. The comparison between experimental and theoretical values reveals the following features: |
 |
| • For both US & SUB cases of both S1 & S2 series there is very close agreement between the experimental values and the values as obtained from terzaghi formula. |
| • For S2 series experimental values especially for US case are very close to values calculated from IS code & Hazens method. |
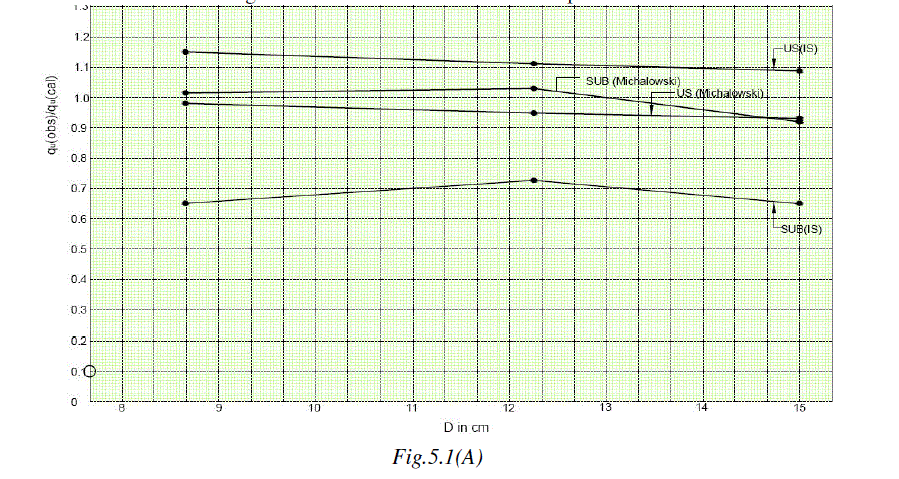
| The values of ratio qu(obs)/qu(cal) are shown in Table 5.1. These are graphically represent in Fig.5.1(A) & 5.1 (B). The following features are observed from these representations: |
 |
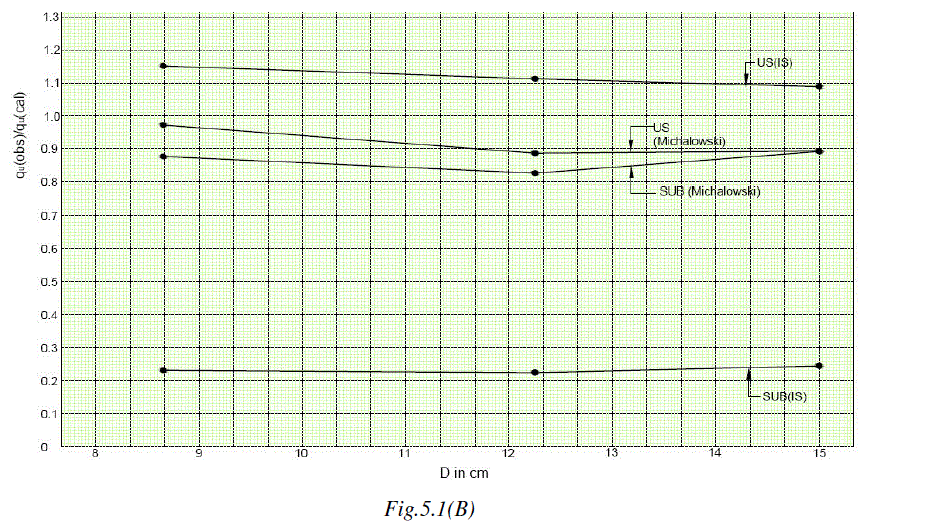 |
| 1) For S1 (90%) Soil in US condition the closeness of the ratio to 1 is seen when qu is computed by Terzaghi's Method. In this value almost ranges from 1.01 to 1.06. |
| 2) For S1(90%) SUB condition the closeness of ratio to 1 is seen when qu is computed by Michalowski method. In this value almost ranges from 0.92 to 1.02 |
| 3) For S2 (75%) Soil in US condition the closeness of the ratio to 1 is seen when qu is computed by Terzaghi's Method. In this value almost ranges from 1 to 1.01 |
| 4) For S2 (75%) SUB condition the closeness of ratio to 1 is seen when qu is computed by Hansen method. In this value almost ranges from 0.97 to 1.04. |
| The above mentioned result point out to the fact that estimation of the above mentioned result point out to the fact that estimation of ultimate bearing capacity is to be done by different approaches for realistic estimation of the result. In other words the choice of method of Computation obviously depends on unsaturated or submerged case of the soil and the initial physical state of the soil (w.r.t. its initial degree of saturation) when it is under unsaturated case. |
| 5.4 Effect of Soil Submergence on Ultimate Bearing Capacity: |
| The evaluation is proposed to be characterised by the following ratio, termed as soil submergence factor, FSUB |
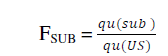 |
| From the experimental investigation this factor was evaluated considering only the experimental value of qu(SUB) and qu(US).. Also the ratio (i.e. FSUB) was computed w.r.to qu values as per I.S. code procedure and the Michalowski's method. Thus theoretical values of the factor by both the approaches were worked out. All these values of the factor in all the cases of experimentation are shown in Table 5.6. The following observations are evident from the tabulated values: |
| ïÃâ÷ It is seen that for particular case of soil foundation system the size the foundation has almost no effect on the ratio, |
| ïÃâ÷ The values of FSUB (as worked out considering various model footing sizes) are given in Table 5.1. It is seen that the experimental values of FSUB tallies well with theoretical values as per I.S. code in case of S1 soil, while for S2 soil (at various initial saturation conditions) there is close agreement between observed FSUB and theoretical FSUB as per Michalowski’s method. |
 |
| ïÃâ÷ The effect of submergence on ultimate bearing capacity (qu) is observed to depend on the initial state of the soil w.r.t. its water content or specially the degree of saturation. |
| ïÃâ÷ In the investigation the soil is taken with two different degree of saturation i.e. Sr = 90% & Sr =75% from table 5.1 it is evident that the full submergence of soil reduces the ultimate bearing capacity by 40% and 80% for initial saturation of 90% & 75% respectively. |
| In general, lower the initial degree of saturation higher is the percentage reduction in qu of submergence, whereas higher initial degree of saturation causes lesser % of reduction in ultimate bearing capacity on full submergence. |
| The aforesaid character may be explained on the basis of the role played by fines. When the soil has high degree of saturation, especially when the water content is more than OMC, the very soft silt clay matrix in the soil causes the soil to become softer and softer, thereby causing its ultimate bearing capacity to be lesser and lesser. And hence when such qu (US) value is the small, the reduction on submergence will be of smaller value. |
VI. CONCLUSION |
| The analysis and interpretation of the results revealed the following noteworthy conclusions: |
| 1. The load-settlement curves for full submergence cases are well below the curves for unsaturated condition, indicating weakened soil support due to rise in WT. Consequently, the ultimate bearing capacity for submerged foundation soil, qu(SUB), is reduced. However, this reduction in bearing capacity depends on: |
| ïÃâ÷ Initial degree of saturation of the soil or its degree of saturation Sr, under unsaturated case. |
| 2. The effect of soil submergence on ultimate bearing capacity of footing Foundation is proposed to be characterized by soil submergence factor FSUB expressed as : |
| 3. For the soil- foundation system of surface circular footing on a c-φ soil, other parameters remaining the same, the size of foundation (i.e. diameter of footing) |
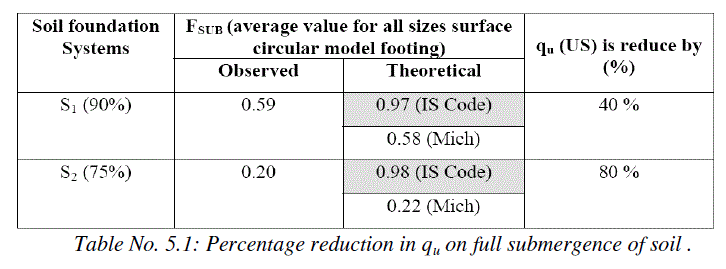 |
| 4. In the study of model footing it is found that in case of S1=90%, the reduction in the ultimate bearing capacity was 39%. Furthermore for same soil when initial degree of saturation was pertaining to Sr of 75 % the bearing capacity got reduced by 80% as shown in table no 6.1.. |
| 5. For computing the value of qu either for US or SUB condition it is of utmost important to precisely determine the respective values of c- φ parameters, pertaining to initial degree of saturation of the soil for US case or for SUB condition. It is found that φ values especially are significantly different for different initial degree of saturation states of soil controlling the qu(US) and qu(SUB). The bearing capacity factors and shape factors need to be determined for the respective values of φ. |
| 6. The extent of difference between the two curves (US and SUB) appears to depend, the Initial physical state of the soil (i.e. in US case) with respect to the degree of saturation and also the size of the circular model footing. |
References |
|