Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

The Solution of Instability Phenomenon Arising in Homogeneous Porous Media by Crank-Nicolson Finite Difference Method

Ravi N. Borana1, V. H. Pradhan2, and M. N. Mehta3
  1. Associate Professor, Department of Mathematics, Bhavan’s Sheth R. A. College of Science, Ahmedabad, India
  2. Associate Professor, Department of Applied Mathematics and Humanities, S. V. N. I. T., Surat, India
  3. Professor, Department of Applied Mathematics and Humanities, S. V. N. I. T., Surat, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

During secondary oil recovery process, when water is injected in oil formatted area to recover remaining oil, the important phenomenon Instability (fingering) occurs due to the injecting force, difference of viscosity and wettability of the water and oil gives rise to the protuberances (instability) at common interface. The injected water will shoot through the porous medium at relatively high speed through the inter connected capillaries and its shape is as good as fingers, therefore it is also called fingering phenomenon and fingers are unstable due to the injecting force, so it is also known as instability phenomenon. The mathematical formulation yields to a non-linear partial differential equation known as Boussinesq equation. Its solution has been obtained by using unconditionally stable Crank-Nicolson finite difference scheme with appropriate initial and boundary conditions. The solution has been compared with the solution of this phenomenon. It is concluded that the solution obtained is very close to the solution obtained by finite element method and analytical method. The solution represents saturation of injected water which is increasing as length of fingers x -increases for given time t  0. The solution represents saturation of injected water occupied by average cross-sectional area of schematic fingers for instability phenomenon. The Matlab coding is used for numerical values and graphical presentation of the solution.

Keywords
Water-flooding process, Instability, immiscible displacement, Crank-Nicolson finite difference scheme, flow through porous medium.

INTRODUCTION
The natural oil field is very large to study the effect of water injection (water flooding) in oil recovery process. In primary recovery process the oil is recovered by natural pressure but after sometime this recovery process does not effect. Hence, the remaining oil from oil basin may be recovered from oil formatted porous medium by injecting different fluids like water, gas, steam and polymer in secondary oil recovery process.
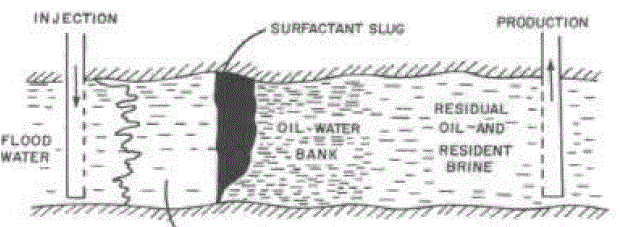image'
Fig. 1 Actual formation of Secondary oil recovery process
To study this effect many authors have studied this phenomenon by choosing small cylindrical piece of porous matrix from large natural oil basin with three sides are impermeable except one end. For the sake of mathematical study, for one-dimensional study of displacement process, taking vertical cross-sectional area of the cylindrical piece of porous matrix of length L which is shown as rectangle having irregular fingers in right side of common interface x 0 (figure 2), Scheidegger and Johnson [15] suggested to replace irregular fingers by schematic fingers of rectangular shape which is shown by the figure 4. They considered average crosssectional area occupied by schematic fingers, as saturation of injected water which is shown by rectangle in right side of common interface x 0 (figure 4).
image'
Fig. 2 The formation of natural fingers during instability phenomenon in the porous medium
The present paper describes instability (fingering) phenomenon in double phase flow of two immiscible fluids (water and oil) through homogeneous porous medium. The displacement of native oil by another of lesser viscosity injected water provides a well-developed finger. Thus, when injected water flowing through porous medium and displacing native fluid oil, then instead of regular displacement of whole front, protuberances (fingers) take place which shoots through the porous medium at relatively very high speed. In the present paper our interest is to solve non-linear partial differential equation for one-dimensional instability phenomenon arising in homogeneous porous medium during secondary oil recovery process. The numerical solution of this equation has been obtained by using Crank-Nicolson scheme of finite difference method and the solution has been compared with the numerical solution by Finite Element Method and Exact solution obtained by analytical method.

II. RELATED RESEARCH WORK
The instability phenomenon in double phase flow of two immiscible fluids (water and oil) through homogeneous porous medium has been discussed in various aspects and from a different view points by number of eminent scholars and researchers. The injected water, intended to push the native fluid forward, tends to penetrate the more viscous native oil through spontaneously formed multi-branched fingers (Marle, 1981) [5]. Saffman and Taylor (1958) derived a classical result for the shape of finger in the absence of capillary. Scheidegger (1960) [14] considered the average cross-sectional area occupied by the fingers while the size and shape of the individual fingers were neglected. Scheidegger and Johnson (1961) [15] discussed the statistical behaviour of instabilities in homogeneous porous media without capillary pressure. Verma (1969) [19, 20, 21, 22] has discussed the statistical behavior of the fingering phenomenon in a displacement process in heterogeneous porous medium with capillary pressure using perturbation solution. The shape, size and velocity prediction of fingers occurring in this phenomenon has been studied, under different situations with different viewpoints by many researchers and engineers from petroleum industry for optimising secondary oil recovery process. Lange et al., 1998; Brailovsky et al., 2006; Zhan and Yortsos, 2000 Wang and Feyen, 1998 and Brailovsky et al. (2006) [2] numerically formulated a non-linear evolution equation for water oil displacement front. They discussed to control the unrestricted growth of fingers by the injection of water not uniformly but rather during suitably distributed intervals of time. Mukherjee and Pinki (2009) have obtained an analytical solution of fingering phenomenon arising in fluid flow through porous media by using techniques of calculus of variation and similarity theory.
Mehta and Yadav (2009) [7], Joshi and Mehta (2009) [8], Meher and Mehta (2011) [9] , Pradhan and Mehta (2011) [10], Mehta and Kinjal (2011) [11], and Mehta and Vyas (2013) have discussed the solution of the Instability phenomenon arising in fluid flow through porous media by the different methods like Group Invariant, Power Series, Finite Element, Lie theoretic approach.

III. STATEMENT OF THE PROBLEM
To study the phenomenon of instability in homogeneous porous medium we choose a cylindrical piece of porous matrix of length L whose three sides are impermeable except one end, from where water is injected. For mathematical study we take vertical cross-sectional area of this cylindrical piece of porous matrix which is rectangle and open end will be the common interface x 0 . Let the water be injected at x 0 then due to the injecting force and viscosity difference the protuberances or instability may arise which is due to the displacement of oil by water injection through inter connected capillaries. The length x of the fingers is being measured in the direction of displacement. Scheidegger and Johnson [15] suggested replacing these irregular fingers by schematic fingers of rectangular size.
image'
Fig. 3 The formation of fingers in the cylindrical piece of porous medium For the sake of mathematical study, consider the average cross-sectional area occupied by schematic fingers as a saturation of injected water for the average length of schematic finger x 0 , for the given time t  0.
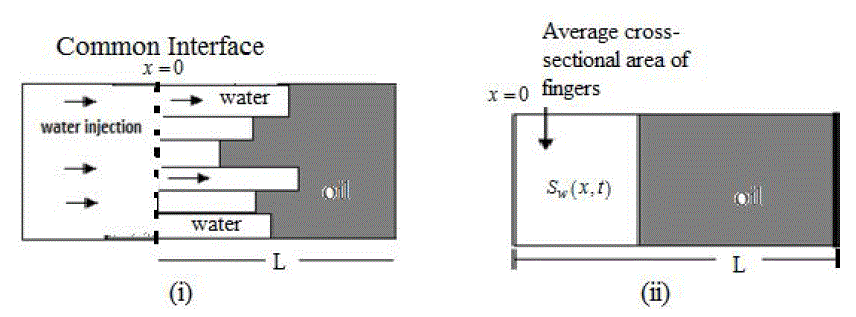image'
Fig. 4 (i) Schematic representation of the fingers and (ii) Average cross-sectional area of the fingers in the rectangular porous matrix.

IV. MATHEMATICAL FORMULATION
When water is injected, at common interface x 0 the oil will be displaced from the porous medium. Hence, seepage velocities of injected water (Vw) and native oil (Vo) are expressed by Darcy’s law (1856) for these two immiscible fluids as Bear (1972) [1],
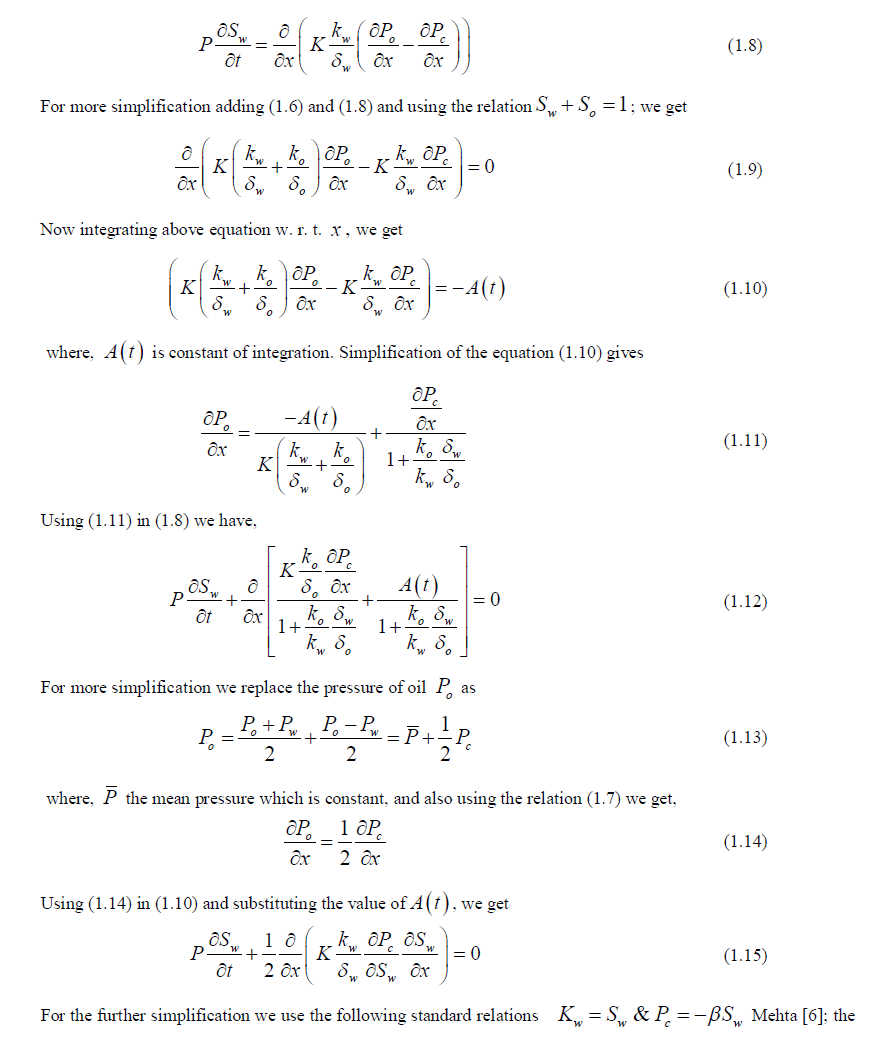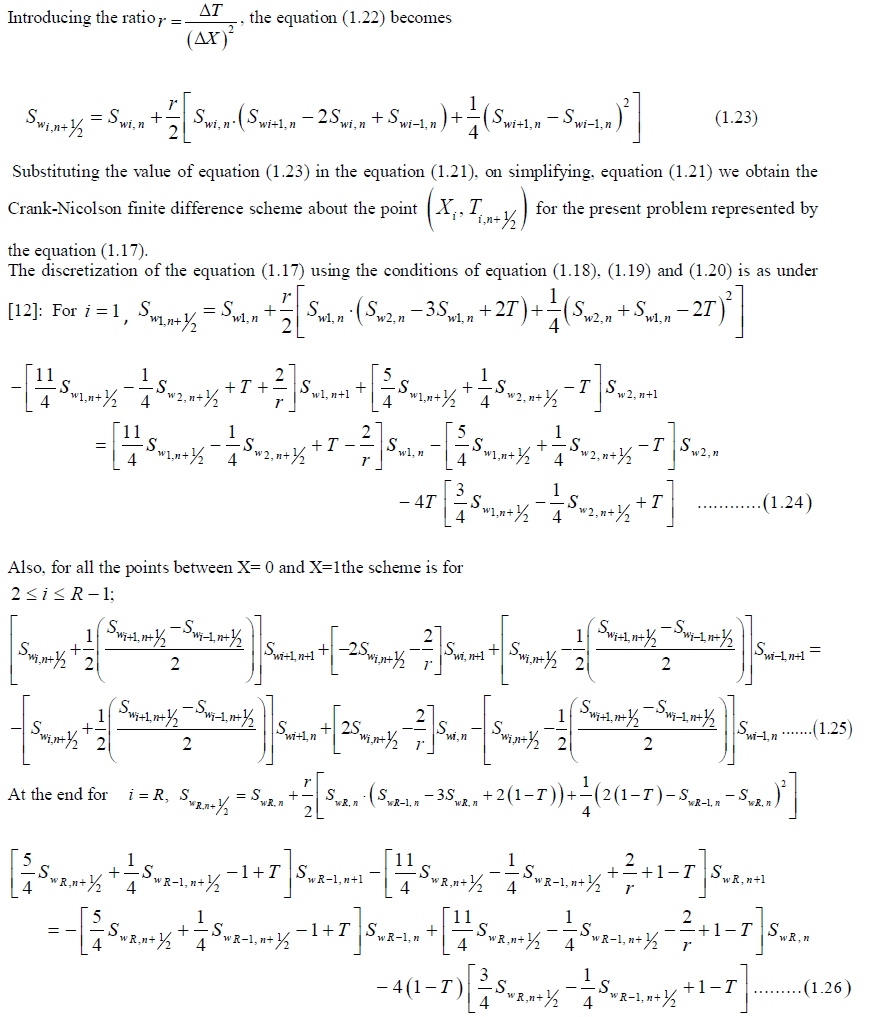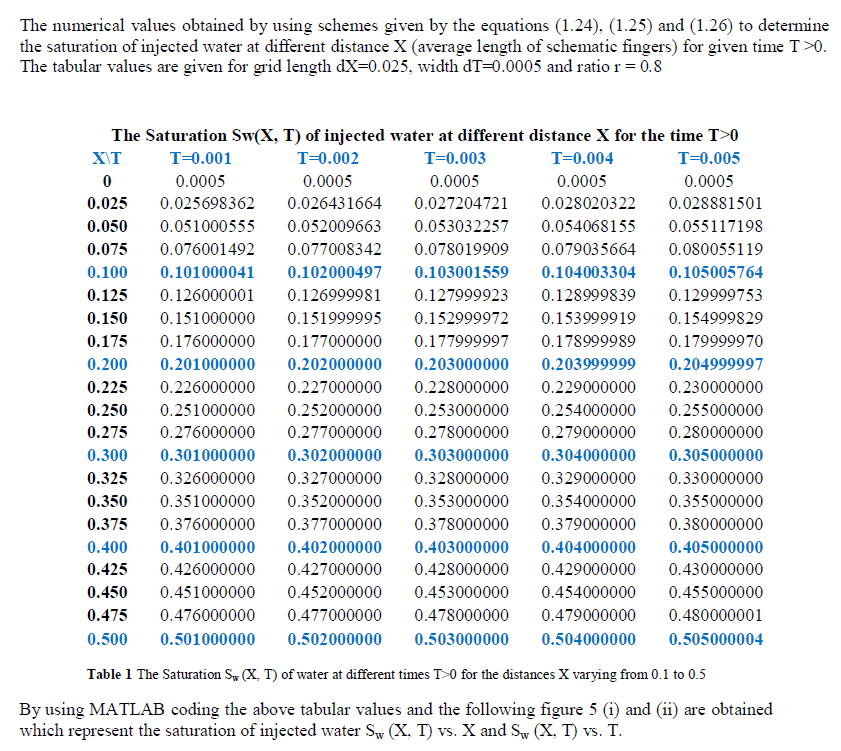image
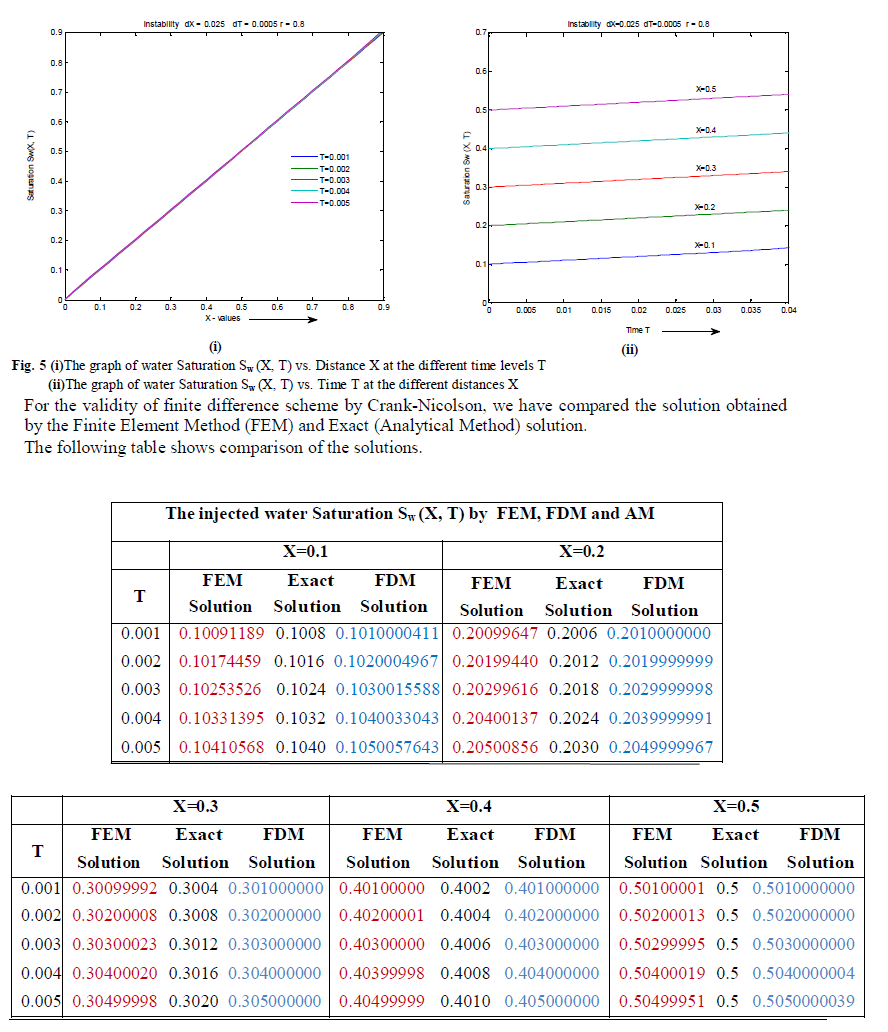
image
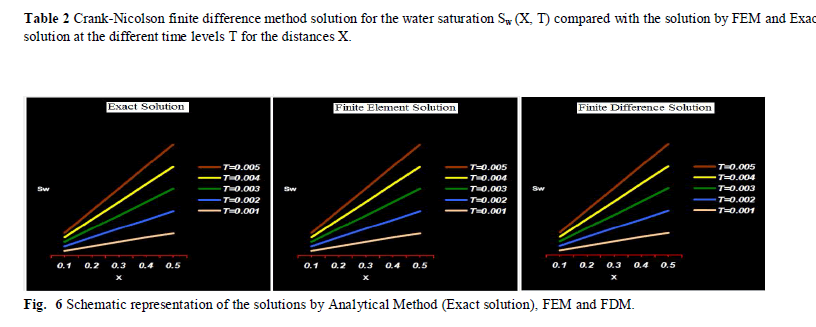image
image
image
image'4
image

VI. CONCLUSION
The tabular values and graphical presentation obtained by using Matlab coding for the finite difference scheme of the equation (1.17) by Crank-Nicolson method shows that the saturation of injected water is linearly increasing as distance X (average length of schematic finger) increases for different time T > 0 and also, it is linearly increasing for increasing time T for different length of the fingers. The comparative study shows that the numerical solution obtained using Crank-Nicolson scheme of finite difference method is very closed to the solutions obtained by finite element method and analytical method for different value of X and time T. From the above discussion we have concluded that saturation of injected water is linearly increasing in instability phenomenon when water is injected at common interface, which serves the purpose of oil recovery in secondary oil recovery process which can displace the oil toward production well, kept in right side of common interface x 0 and near to end x L . This also concludes that the validity of the Crank-Nicolson finite difference scheme applied in secondary oil recovery process.

ACKNOWLEDGEMENT
I am deeply thankful to my mother institute Bhartiya Vidhya Bhavan, Ahmedabad Kendra for giving me an opportunity to pursue Ph. D. research work. I am very much indebted and grateful to my mathematical and spiritual master former Head of the Department Prof. V. R. Trivedi (Swamiji) for his invaluable and incredible inspiration, blessings and just being by my side all the time.

References
  1. Bear, J., “Dynamics of Fluids in Porous Media”, American Elsevier Publishing Company, Inc., 1972.
  2. Brailovsky, I., Babchin, A., Frankle, M., and Sivashinsky, G., “Instability in water-oil displacement. Transport in porous media”, Vol. 63, pp. 380-393, 2006.
  3. Crank, J., and Nicolson, P., “A Practical Method for Numerical evaluation of Solutions of Partial Differential Equations of the heat conduction type”, Proc.Camb. Phil. Soc. 43, pp. 50-67, 1947.
  4. Donaldson, E. C., Chilingarian, G. V., and Ten Fu Yen, “Enhanced Oil Recovery-II process and operations”, Elsevier Science Publishing Co. Inc., 1989.
  5. Marle, C. M., “Multiphase flow in porous media”, Editions Technip, pp. 220-240, 1981.
  6. Mehta, M. N., “Asymptotic expansion of fluid flow through porous media”, Ph. D. thesis, South Gujarat University, 1977.
  7. Mehta, M. N., and Yadav, S., “Classical Solution of Non-Linear Equations Arising in Fluid Flow through Homogenous Porous Media”, Ph. D. thesis, SVNIT, 2009.
  8. Mehta, M. N., and Joshi M. S., “Solution by Group Invariant method of Instability phenomenon arising in fluid flow through porous media”, International Journal of Engineering Research and Industrial Applications, Vol.2, pp. 35-48, 2009.
  9. Meher, R., Mehta, M. N., and Meher, S. K., “Instability phenomenon arising in double phase flow through porous medium with capillary pressure”, International J. of Applied Mathematics and Mechanics, Vol. 7, Issue 15, pp. 97-112, 2011.
  10. Pradhan, V. H., Mehta, M. N., and Patel, T., “A numerical solution of nonlinear equation representing one dimensional instability phenomena in porous media by finite element technique”, IJAET, Vol. 2, pp. 221-227, 2011.
  11. Patel, K., Mehta, M. N., and Patel, T., “The power series solution of Fingering phenomenon arising in fluid flow through homogeneous porous media”, Applications and Applied Mathematics, Vol. 6, Issue 2, pp. 497-509, 2011.
  12. Rosenberg, D. U., “Methods for the Numerical Solution of Partial Differential Equations”, American Elsevier Publishing Company, Inc., 1969.
  13. Richtmeyer, R. D., and Morton, K.W., “Difference Methods for Initial-Value Problems”, 2nd ed., Wiley-Interscience, 1967.
  14. Scheidegger, A. E., “Growth of instabilities on displacement fronts in porous media”, Physics of Fluids, No. 3, pp. 94, 1960.
  15. Scheidegger, A. E., and Johnson, E. F., “The statistical behaviour of instabilities in displacement process in porous media”, Canadian J. Physics, pp. 319-326 1961.
  16. Scheidegger, A. E., “The physics of flow through porous media”, 3rd ed., University of Toronto Press, pp. 216, 1974.
  17. Smith, G.D., “Numerical Solution of Partial Diff. Equations Finite Difference Methods”, 3rd ed., Oxford Uni. Press, 1965.
  18. Thomas, J. W., “Numerical Partial Differential Equations-Finite Difference Methods”, Springer-Verlag, 1995.
  19. Verma, A. P., “Statistical behaviour of fingering in displacement process in heterogeneous porous medium with capillary pressure”, Canadian Journal of Physics, pp. 3, 47,319, 1969.
  20. Verma, A. P., and Mishra, S. K., “Similarity solution for instabilities in double‐phase flow through porous media” Journal of Applied Physics, Vol. 44, pp. 16-22, 1973.
  21. Verma, A. P., “Instabilities in two phases flow through porous media with magnetic fluids”, Multiphase transport- Fundamentals-Reactor safety Applications, Hamisphere publishing Company, Vol. 5, pp. 1323-1335, 1980.
  22. Zhangxin, C., Gaunren, H., and Yuanle, M., “Computational methods for multiphase flows in Porous Media”, Siam, 2006.