ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| A.UmaMaheswari1, P.Kumari2 Associate Professor in Mathematics, Quaid-E-Millath Govt. College for Women, Chennai, India 1 Assistant Professor in Mathematics, D.G.Vaishnav College,Chennai, India2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper we present a new class of operators based on Trapezoid Fuzzy numbers such as Trapezoid Fuzzy Prioritized Weighted Mean (TFPWM) operator, Trapezoid Fuzzy Prioritized Weighted Geometric Average (TFPWG), Trapezoid Fuzzy Prioritized Weighted Harmonic Average(TFPWH) operators to solve multiple attribute group decision making (MAGDM) problems. Unlike other (MAGDM) techniques here the attributes and experts are at different priority levels. Some desirable properties of TFPWM, TFPWG and TFPWH operator are investigated. Finally, we give a numerical example to illustrate the application of these operators to group decision making problems with trapezoidal fuzzy information.
Keywords |
| Aggregation Operators, Trapezoidal Fuzzy numbers, Prioritized aggregation operators, Decision making. |
INTRODUCTION |
| Multiple attribute decision making methods are widely used to rank many real world alternatives with respect to several competing attributes. Since the decision making process is governed by human perception and judgment which is ambiguous in nature, using fuzzy sets instead of exact numerical values will be a suitable selection in these cases. Due to the increase in complexity of real world decision making environments, most decision making processes takes place in group. The group decision making under fuzzy environment is an interesting research topic and have produced good results [1,2,3]. In many group decisions making situations under uncertainty, because of the ambiguity in human thinking, the information given by the decision makers (DMs) often takes the form of fuzzy numbers. The key step in the process of group decision making is to aggregate these information by using a proper aggregation operator [4,5]. Aggregation operators (AOs) are mathematical functions that are used to combine information [6]. AOs have the ability to fuse the fuzzy information. Different types of AOs are found in the literature [7]. A very common aggregation method is the ordered weighed averaging operator (OWA) [8]. The OWA operators were used for aggregating information expressed as exact numbers. Mostly the information available was imprecise and uncertain which can be expressed as fuzzy numbers. In this context fuzzy OWA (FOWA) operator was introduced to aggregate information represented by fuzzy numbers. The FOWA operator has been in the literature [9,10]. Yager[11] introduced the prioritized aggregation operators which allowed inclusion of priority between the attributes. Zhao[12] investigated the triangular fuzzy multiple attribute group decision making problem using fuzzy prioritized operators. The trapezoidal fuzzy numbers are a more general case encompassing the triangular ones with support in [0,1][13] . Thus the Trapezoid fuzzy numbers are more suitable for use in depicting imprecise or vague fuzzy information. In all MAGDM methods so far developed under trapezoidal fuzzy environment the attributes and DMs are at the same priority level. But in many types of applications we prioritize among the attribute or criteria and also among the DM’s. Yager [11,14] first investigated this kind of issue. In this work we propose some fuzzy prioritized aggregation operators such as TFPWM, TFPWG, TFPWH which allows prioritization among the attribute and DM’s. We have also studied some properties of these operators. In section 2, we briefly review some basic concepts. In sections 3-5 three trapezoid fuzzy prioritized operators TFPWM, TFPWG, TFPWH and their properties are studied. Section 6 demonstrates a procedure for multiple attribute group decision making problems using these operators. Section 7 provides a numerical example to demonstrate the validity and effectiveness of the proposed operators. |
II. BASIC CONCEPTS AND OPERATIONS |
| In this section we briefly recall some basic concepts related to trapezoid fuzzy number and fuzzy OWA operators. |
| A.Definition |
 |
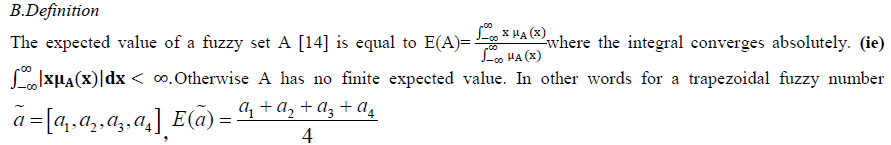 |
| C.Aggregation Operators (AO) |
| Aggregation operators [6] are mathematical functions used to combine different pieces of information. Although there is no standard definition of AOs, an AO of dimension n is a mapping |
| D.OWA Operators |
| Another class of AO’s are the Ordered Weighted Averaging (OWA) operators [8] that provide a parameterized class of mean type AOs. |
An OWA operator of dimension n is a mapping 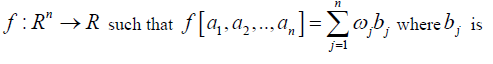 |
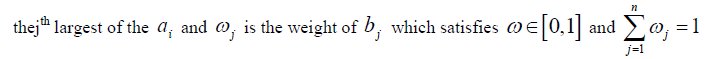 |
| The OWA operator is symmetrical, monotonic, bounded and satisfies idempotency [8] |
 |
III. THE TRAPEZOID FUZZY PRIORITIZED AND WEIGHED MEAN OPERATOR (TFPWM) |
| A. Definition |
| Let |
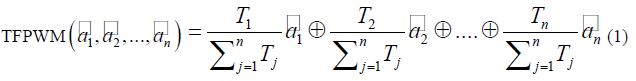 |
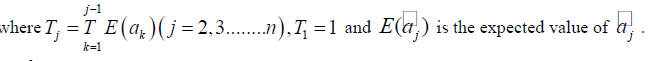 |
| B. Theorem 3.1 |
| Let |
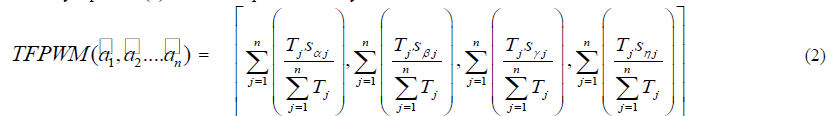 |
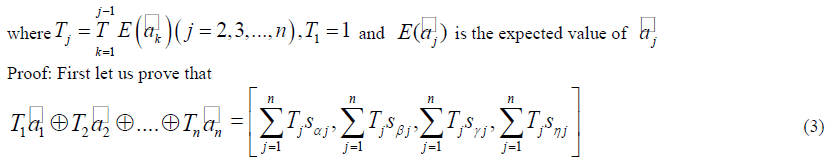 |
| We use mathematical induction to prove the theorem. Since the case of n=1 is trivial let us prove the result for n=2 |
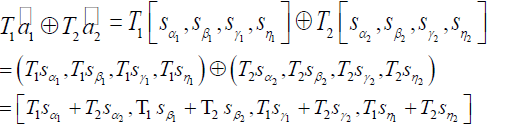 |
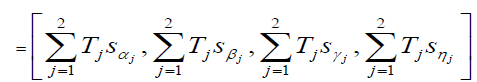 |
| Thus proving the case when n=2. Now assume that equation (2) is true when n=k |
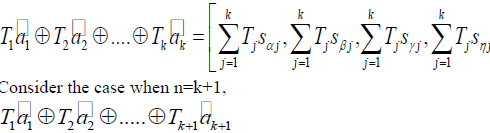 |
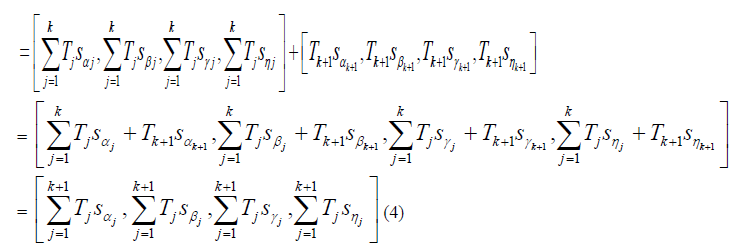 |
| Thus proving equation (3). |
| By equation (1) |
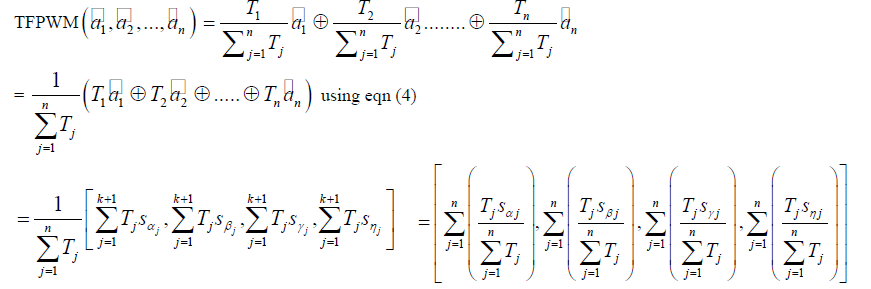 |
| Hence the proof |
| C.Theorem 3.2 (Idempotency) |
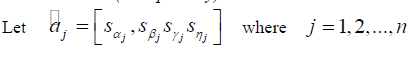 be a set of trapezoidal fuzzy numbers where be a set of trapezoidal fuzzy numbers where |
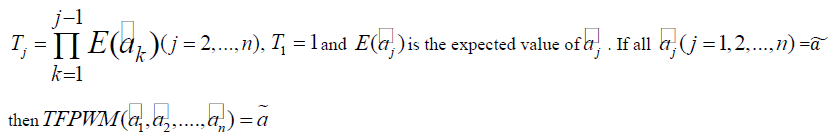 |
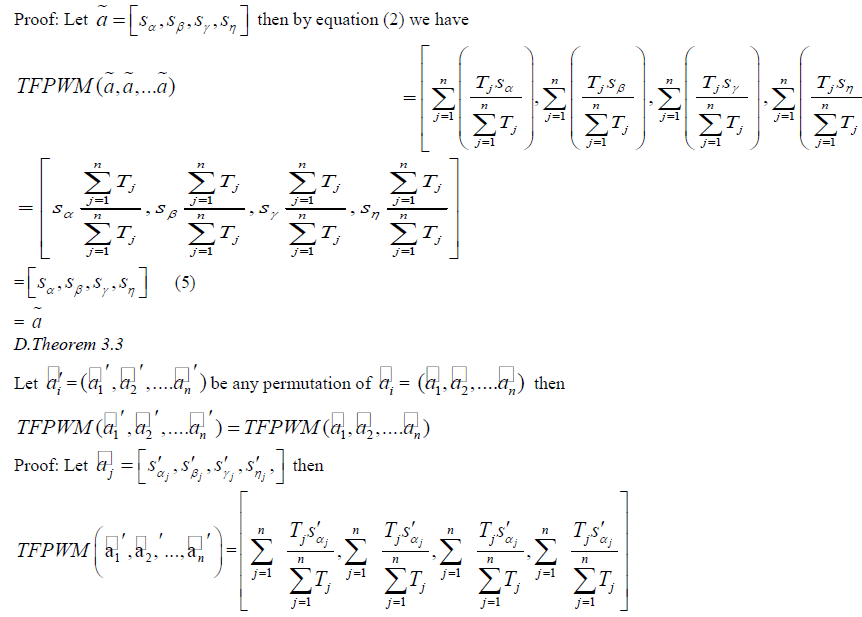 |
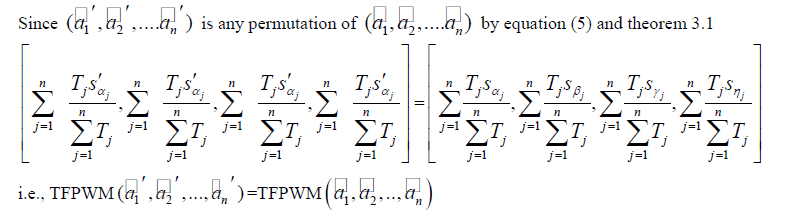 |
| E.THEOREM 3.4 (Monotonicity) |
| Let |
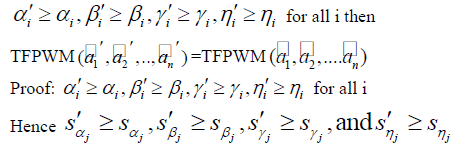 |
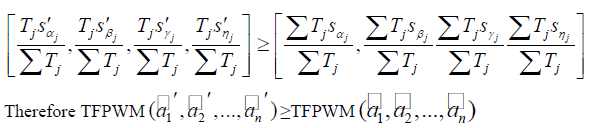 |
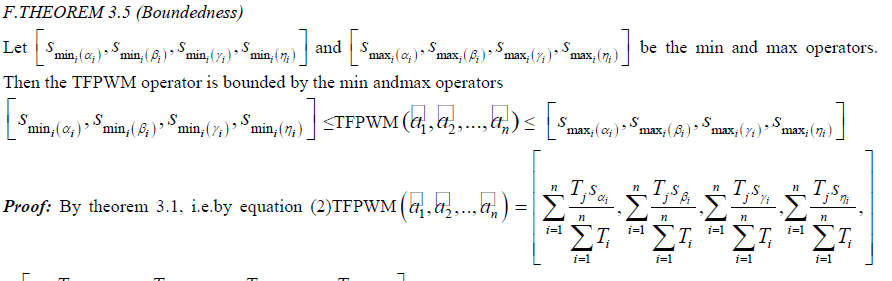 |
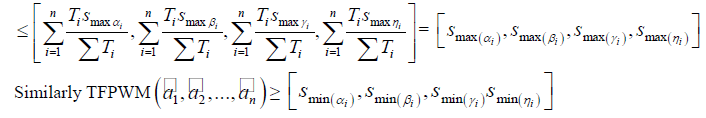 |
IV. THE TRAPEZOID FUZZY PRIORITIZED WEIGHTEDGEOMETRIC OPERATOR (TFPWG) |
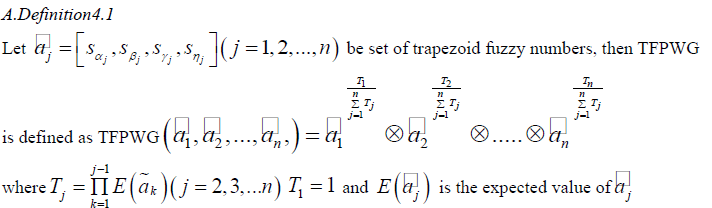 |
| Based on the operations of trapezoidal fuzzy numbers we state the following theorem. B.Theorem 4.1 |
 |
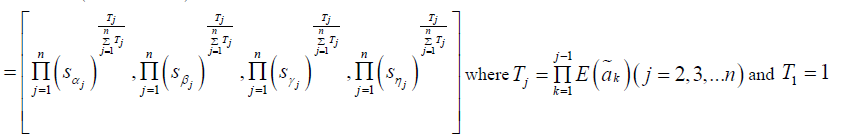 |
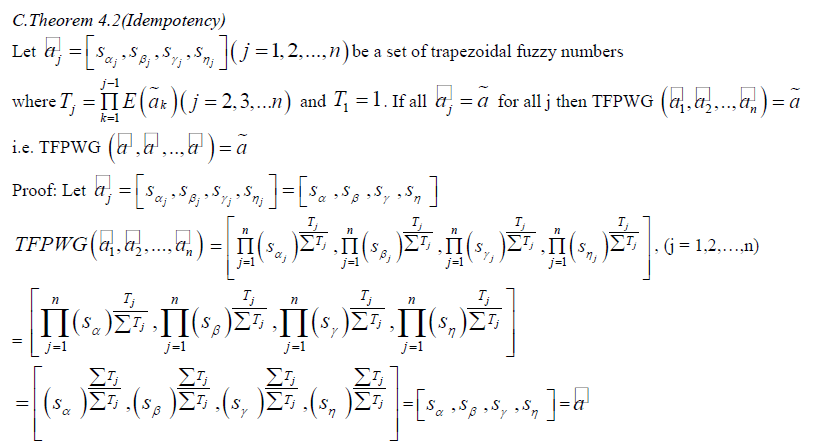 |
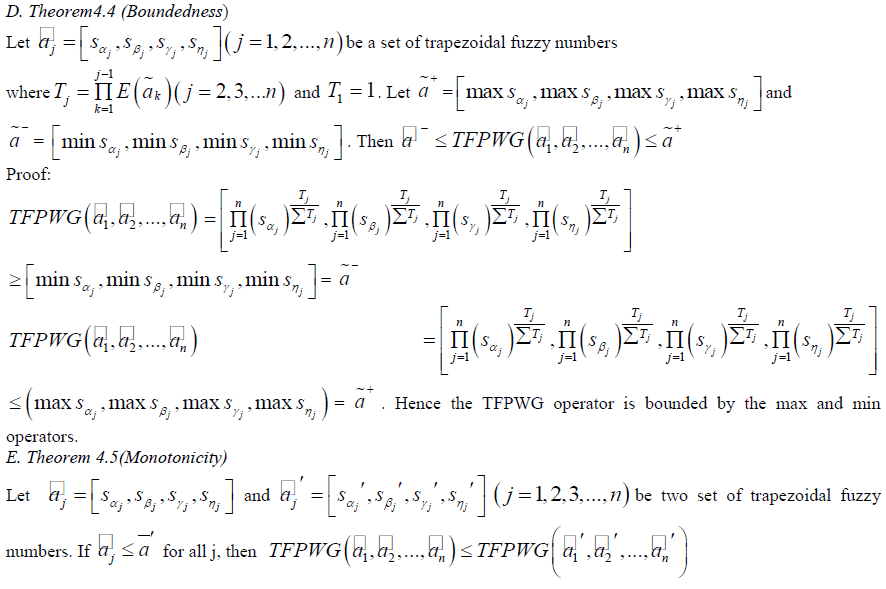 |
V. THE TRAPEZOID FUZZY PRIORITIZED WEIGHTED HARMONIC OPERATOR (TFPWH) |
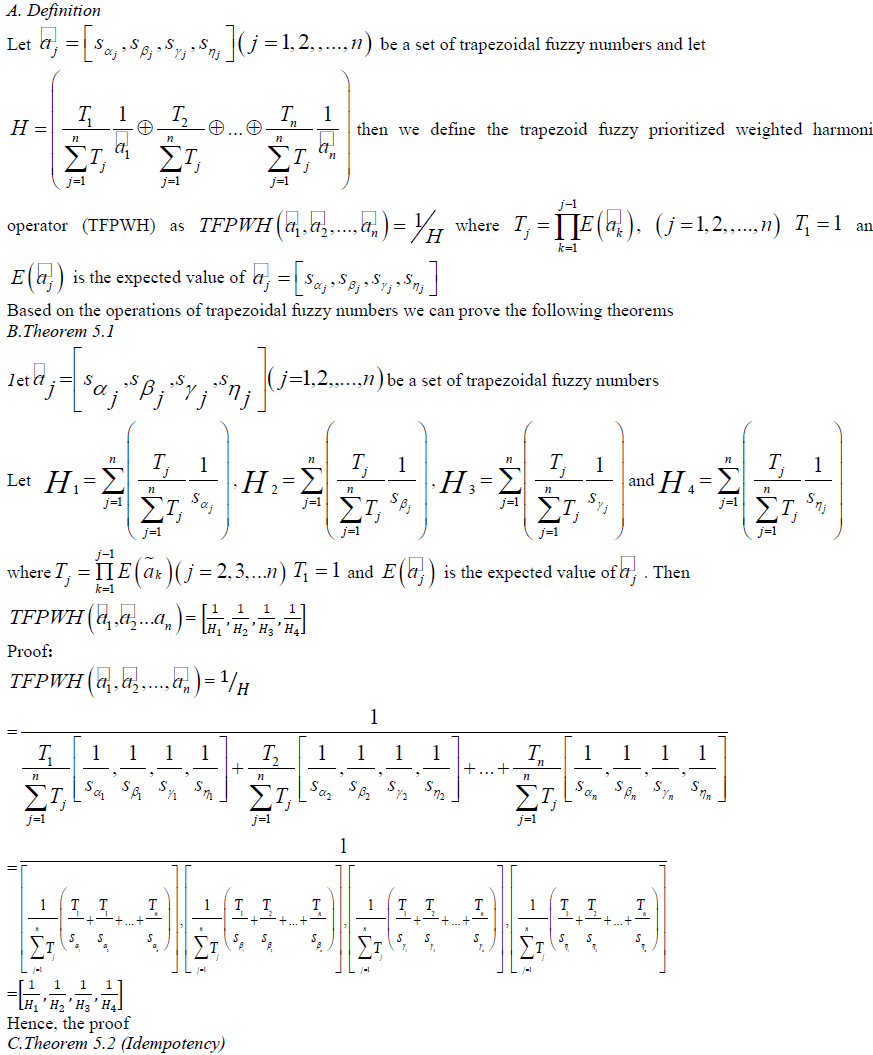 |
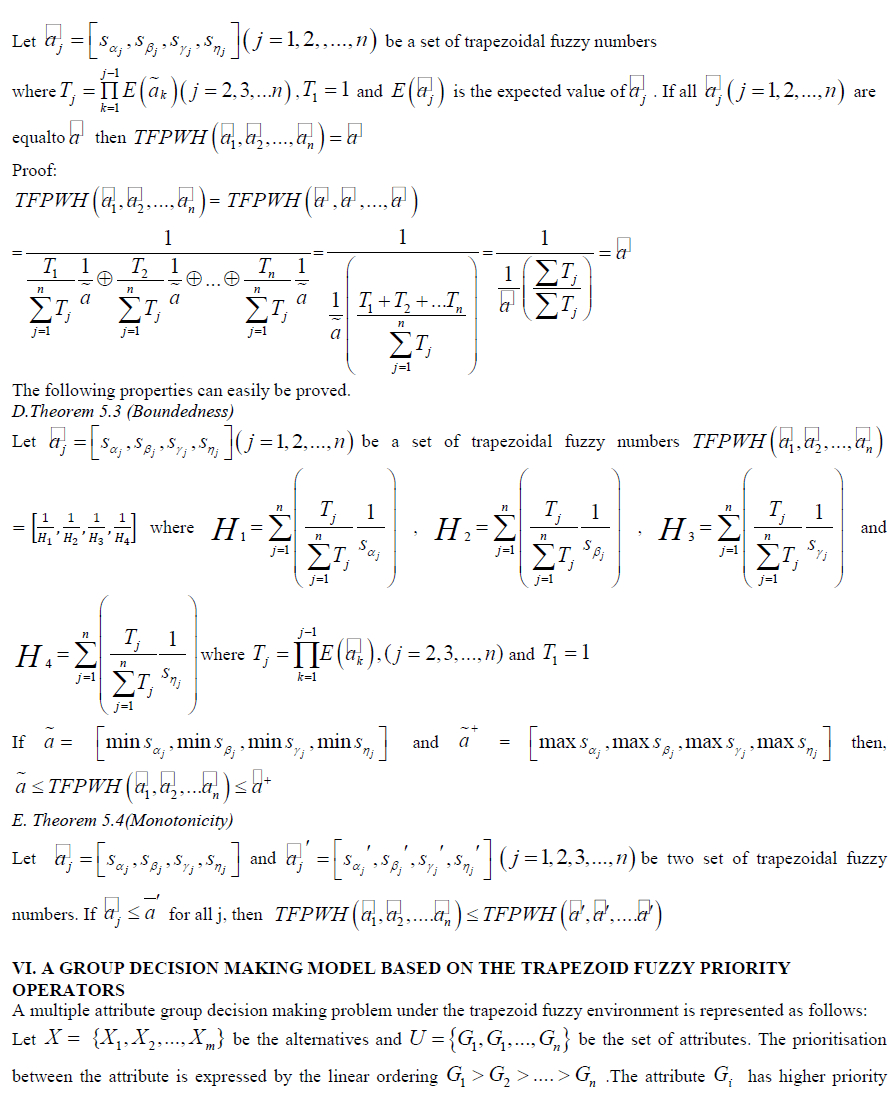 |
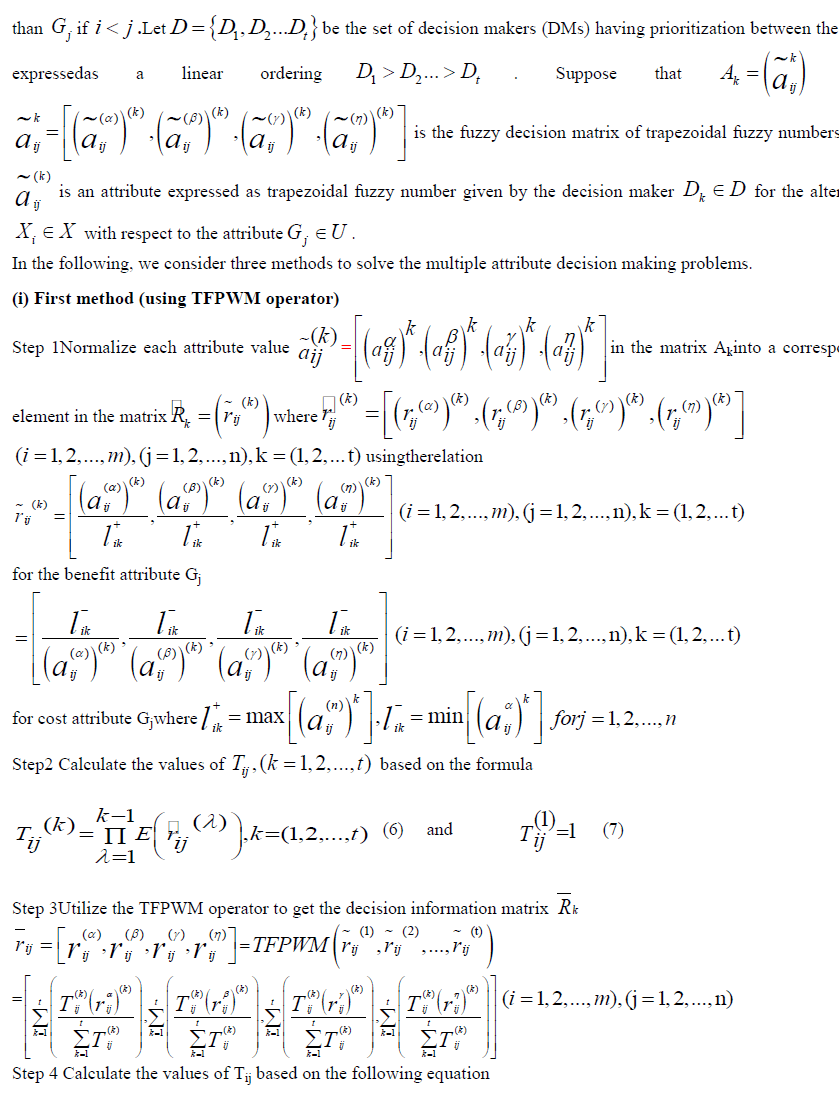 |
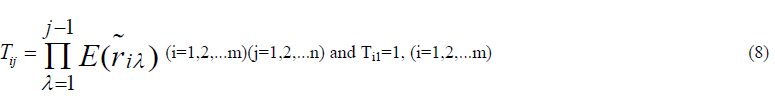 |
 |
| (ii) Second method using TFPWG operator: |
| Step 1 and Step 2 Same as outlined in the first method. |
| Step 3 Utilize the TFPWG operator and the |
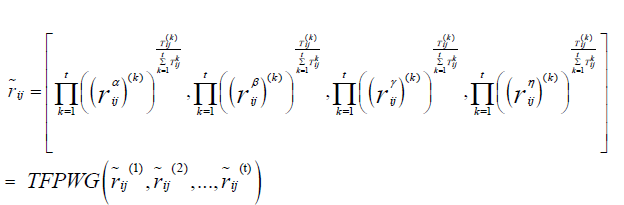 |
| Step 4Same as in first method |
| Step 5: Aggregate the trapezoid fuzzy preference value |
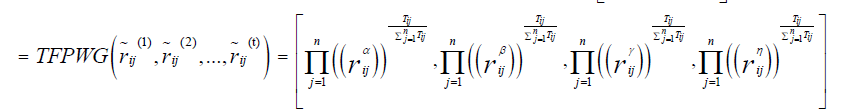 |
| Step 6 and Step 7 same as in first method |
| (iii) Third Method based on TFPWH operator: |
| Step 1 and Step 2Same as in first method |
| Step 3 Utilize the TFPWH operator and the Rk matrix |
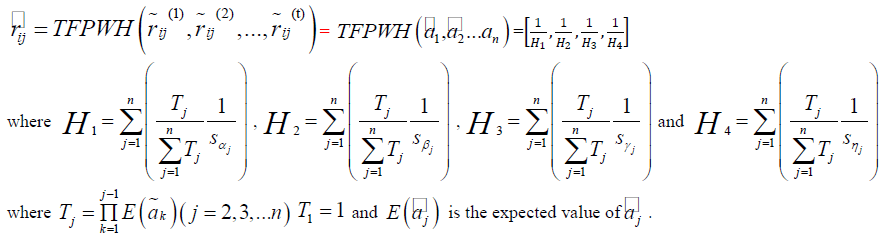 |
| Step 4Same as in first method |
| Step5Aggregate the trapezoid fuzzy preferences value |
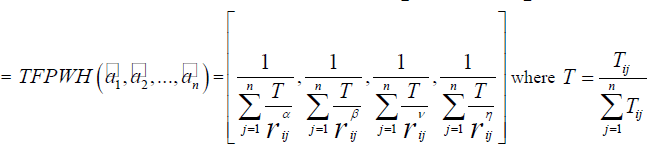 |
| Step 6 & Step 7 Same as in first method. |
VII. ILLUSTRATIVE EXAMPLE |
 |
| Step 1 Four possible candidates are evaluated using trapezoid fuzzy numbers by the three decision makers under the above four attributes and the trapezoid fuzzy decision matrices are shown in Table 1-3. |
 |
| Table 1Decision Matrix A1 |
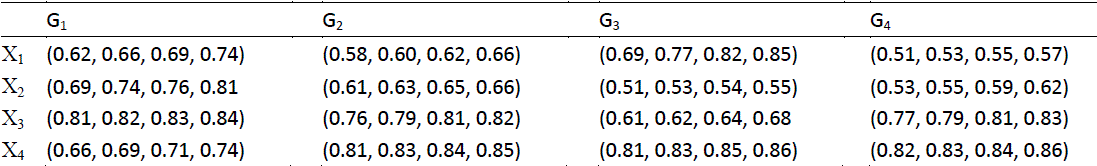 |
| Table 2 Decision Matrix A2 |
 |
| Table-3 Decision Matrix A3 |
 |
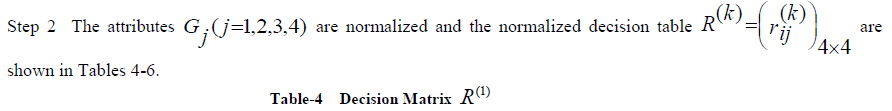 |
 |
| Table-5 Decision Matrix R(2) |
 |
| Table-6 Decision Matrix R(2) |
 |
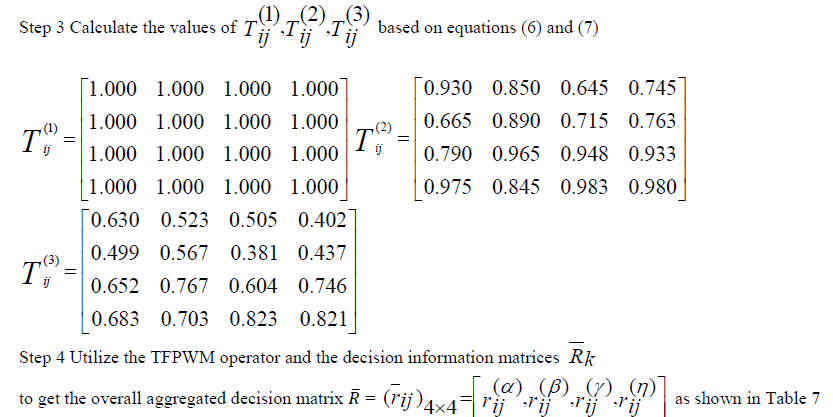 |
 |
| Table 7 Decision Matrix R |
| Step 5 Usingeqn.(8) calculate the values of |
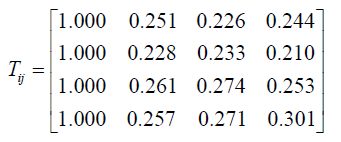 |
| Step 6 Calculate the overall trapezoidal fuzzy preference values |
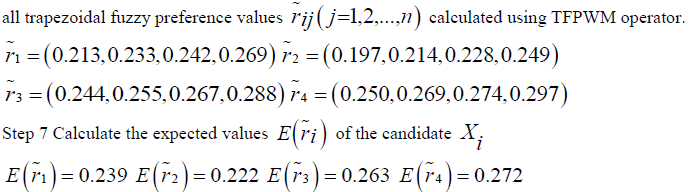 |
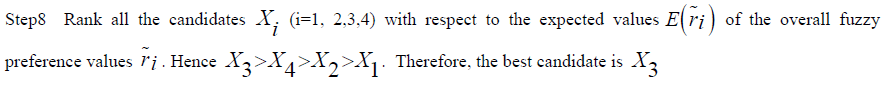 |
| Second method based on the TFPWG operator is described as follows: |
| Step1-3 Refer Step 1-3 of first method |
Step 4 Utilize the TFPWG operator and the decision information matrices Rk to get the overall aggregated decision matrix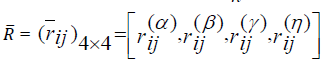 as shown in Table 8 as shown in Table 8 |
 |
 |
VIII.CONCLUSION |
| We have investigated the multi-attribute decision making problems under trapezoid fuzzy environment and developed an approach to handle situations where the attribute and decision makers are at different priority level. We have introduced the Trapezoid Fuzzy Prioritized Weighted Mean (TFPWM) operator, Trapezoid Prioritized Geometric Average (TFPWG) operator and Trapezoid Fuzzy Prioritized Harmonic Average (TFPWH) operator that can aggregate the individual trapezoid fuzzy variables. We have also studied some properties of these operators and illustrated their operational procedure in detail. The utility of these operators can be extended to other domains of data mining, cluster analysis, etc. |
References |
|