Theoretical and Numerical Vibration Study of
Continuous Beam with Crack Size and Location Effect

Dr. Muhannad Al-Waily

Theoretical and Numerical Vibration Study of Continuous Beam with Crack Size and Location Effect

Dr. Muhannad Al-Waily
Faculty of Engineering, Department of Mechanical Engineering, University of Kufa, Iraq

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In this research the natural frequency of a cracked beam with different supported, simply and clamped beam, is investigated analytically and numerically by finite element method with using of ANSYS program ver. 14 with different crack depth and location effect and the results are compared. The analytical results of the effect of a crack in a continuous beam are calculated the equivalent stiffness, EI, for a rectangular beam to involve an exponential function with depth and location of crack effect, with solution of assuming equivalent stiffness beam (EI) by using of Fourier series method. And, The beam materials studied are low carbon steel, Alloys Aluminium, and Bronze materials with different beam length and depth. A comparison made between analytical results from theoretical solution of general equation of motion of beam with crack effect with numerical by ANSYS results, where the biggest error percentage is about (1.8 %). Also it is found that the frequency of beam when the crack is in the middle position is less than the frequency with crack near the end position and the natural frequency of beam decreasing with increasing of crack depth due to decreasing of beam stiffness at any location of crack in beam.

Keywords

Vibration beam, crack beam, health monitoring, theoretical vibration crack beam, frequency of beam with crack effect.

INTRODUCTION

Many engineering components used in the aeronautical, aerospace and naval construction industries are considered by designers as vibrating structures, operating under a large number of random cyclic stresses. Consequently, it is natural to expect that fatigue crack initiation and propagation in critically stressed zones of such structures, in particular when local or general resonance occurs, [3]. The importance of the beam and its engineering applications is obvious, and it undergoes many different of loading. Many types of loading may cause cracks in the beam. These cracks and their locations effect on the shapes and values of the beam frequency. Recently these topics are so prevailing in the industry of spacecraft, airplanes, wind turbines, turbines, robot arm and many other applications. Many studies were performed to examine the vibration and dynamic of cracked beams, as, M. I. Friswell and J. E. T. Penny [1], presented a compares the different approaches to crack modeling, and demonstrates that for structural health monitoring using low frequency vibration, simple models of crack flexibility based on beam elements are adequate. This paper also addresses the effect of the excitation for breathing cracks, where the beam stiffness is bilinear, depending on whether the crack is open or closed. Most structural health monitoring methods assume that the structure is behaving linearly, whereas in practice the response will be nonlinear to an extent that varies with the form of the excitation. This paper will demonstrate these effects for a simple beam structure.

K. El Bikri et. al. [3], presented a theoretical investigation of the geometrically non-linear free vibrations of a clamped– clamped beam containing an open crack. The approach uses a semi-analytical model based on an extension of the Rayleigh–Ritz method to non-linear vibrations, which is mainly influenced by the choice of the admissible functions. The general formulation is established using new admissible functions, called ‘‘cracked beam functions’’, and denoted as ‘‘CBF’’, which satisfy the natural and geometrical end conditions, as well as the inner boundary conditions at the crack location. The work is restricted to the fundamental mode in order to concentrate on the study of the influence of the crack on the non-linear dynamic response near to the fundamental resonance.

D. Sreekanth Kumar et. al. [5], presented a spectral finite element with embedded transverse crack is developed and implemented to simulate the diagnostic wave scattering in composite beams with various forms of transverse crack, such as surface-breaking cracks, matrix cracking and fiber fracture. The equilibrium equations are represented using compact matrix notations. After assembly of the element-internal system of waveguides, the internal nodes are condensed out and finally a two-node finite element in frequency domain is obtained. Important conclusions are drawn on the advantages of the proposed approach, limitations of the element and further scope of improved diagnostic analysis of cracked beam.

Ertugrul Cam et. al. [6], presented information about the location and depth of cracks in cracked beams. For this purpose, the vibrations as a result of impact shocks were analyzed. The signals obtained in defect-free and cracked beams were compared in the frequency domain. The results of the study suggest to determine the location and depth of cracks by analyzing the from vibration signals. Experimental results and simulations obtained by the software ANSYS are in good agreement.

The objective of this paper is to study the effect of crack depth and position on the natural frequency of the beam by using of analytical solution of general equation of motion of beam with crack effect and compared with numerical results evaluated by finite element method with using of Ansys Program.

To achieve the above objectives, analytical solution is developed for dynamic analysis of beam with and without crack effect to evaluate the fundamental natural frequency of beam by using the analytical solution of general equation of motion of beam with crack effect, by building a computer program for analytical solution using Fortran power station 4.0 program.

II. MATHEMATICAL MODEL

Consider the beam shown in Fig. 1, having the following geometrical and material characteristics (l,w, d, dc , E, I x , Ã¯ÂÂ²), where; E-modulus of elasticity; and Ã¯ÂÂ²-density of beam and other notations as shown in the figure. The beam is supposed to be loaded with a bending moment and to have a uniform transverse surface crack of depth a located at a given position xc from the left edge of the beam.

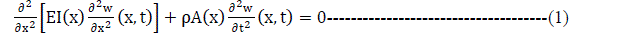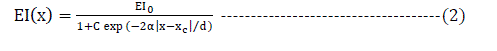By using of the building a computer program for analytical solution using Fortran power station 4.0 program, can be get the results of Eq. (15) to evaluated natural frequency of beam.

III. NUMERICAL MODEL

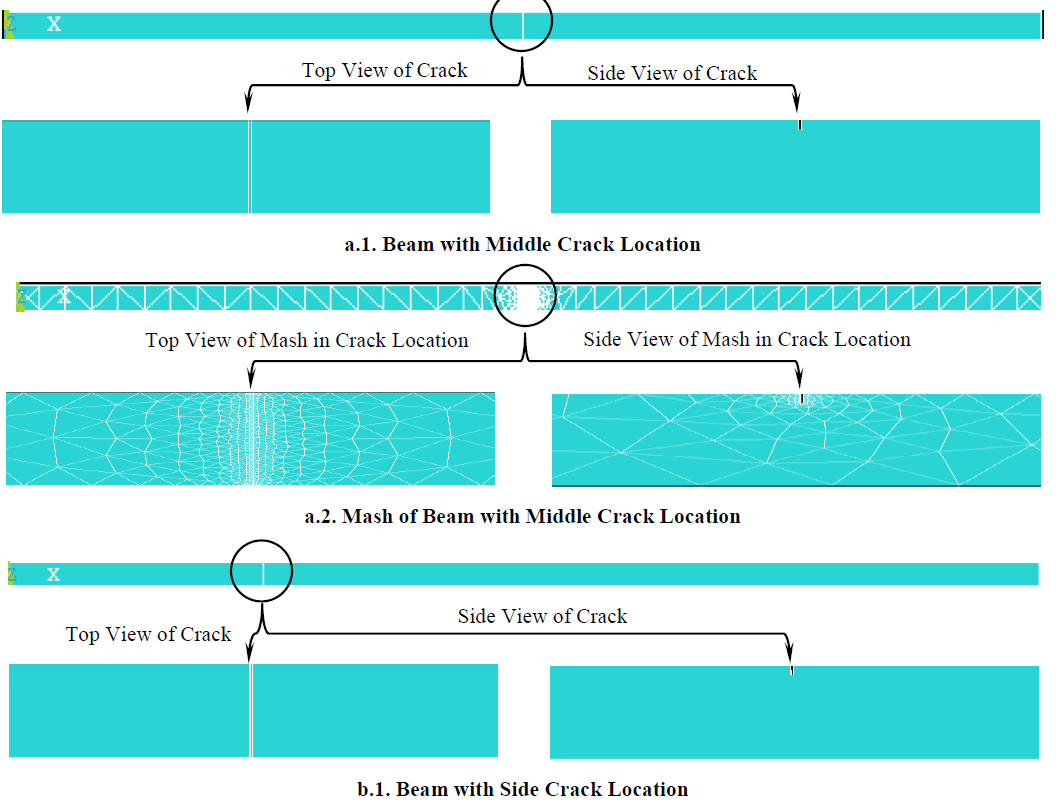
In this method, the finite elements method was applied by using the ANSYS program (ver.14). The three dimensional model were built and the element (Solid Tet 10 node 187) were used.

Generally the number of nodes was approximately (1250-1300) and the number of elements was (550-600). A sample of meshed beam is shown in Fig. 2. for different crack location and depth.

IV. RESULT AND DISCUSSION

The vibration results of beam with crack effect includes the evaluation of the natural frequency of different beam dimensions and materials, with crack effect of beam, included the effect of crack size, crack location, and other parameters of beam as length, depth and boundary condition of beam.

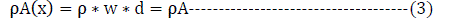The method studied to evaluated the natural frequency of beam with crack effect are, theoretical study and numerical study, by using ANSYS Program Version 14.

The theoretical work includes the study of the crack effect of beam with different crack size (depth of crack), different crack position, different beam dimensions (depth and length of beam) and simply supported boundary conditions of beam.

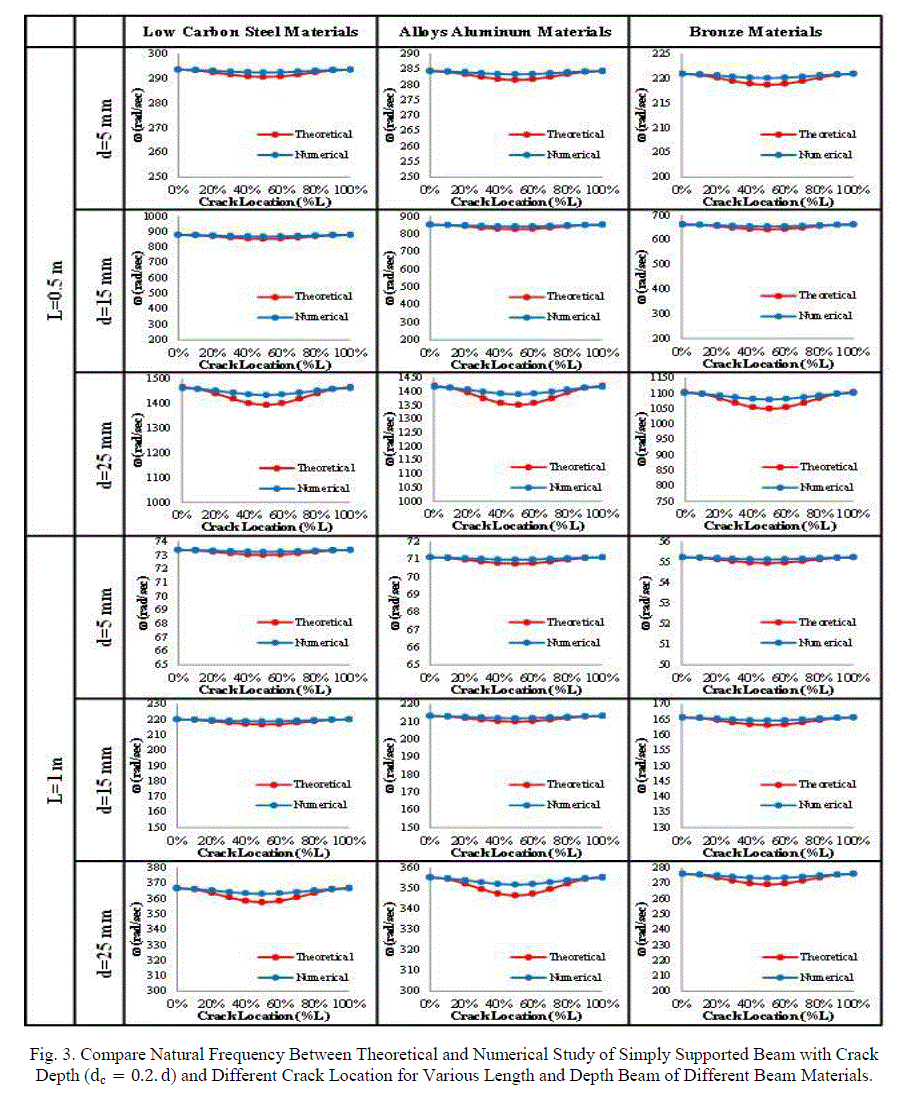
The theoretical results are compared with those obtained numerically by using the ANSYS Program (Version 14) for each parameters effect studied as shown in Figs. 3 and 4. A comparison made between analytical results from solution of general equation of motion of beam, with crack effect, with numerical results by finite elements methods, shows a good approximation where the biggest error percentage is about (1.8 %).

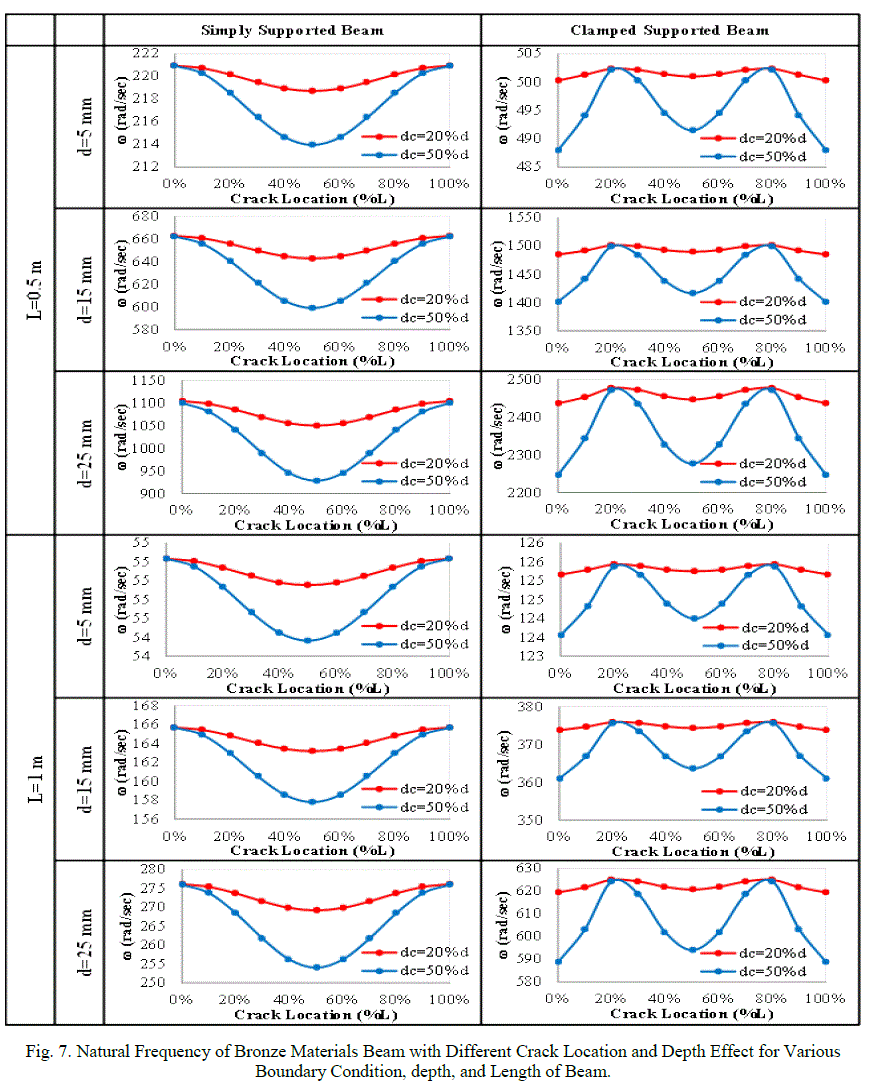
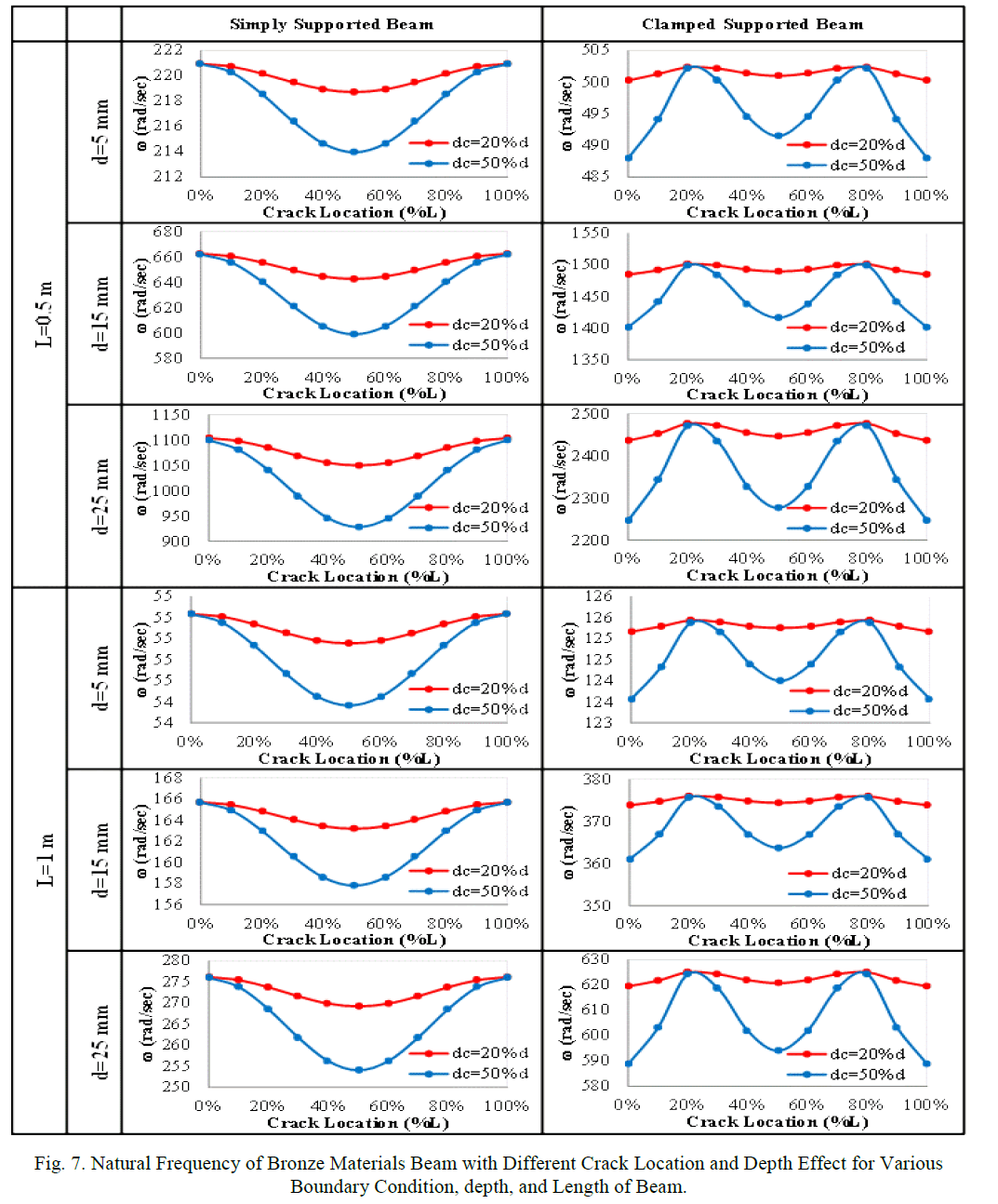
The effect of crack size as depth of crack for beam with different length, depth, and boundary conditions of different beam materials, with different location of crack are shown in figs. 5 to 7. From Figs. 5 to 7 shows the effect of the crack on the natural frequency of beam, can see that the natural frequency decreasing with increasing crack depth for different crack position, this is because the changing in stiffness beam. And the rate of decreasing for experimental are close for different crack position.

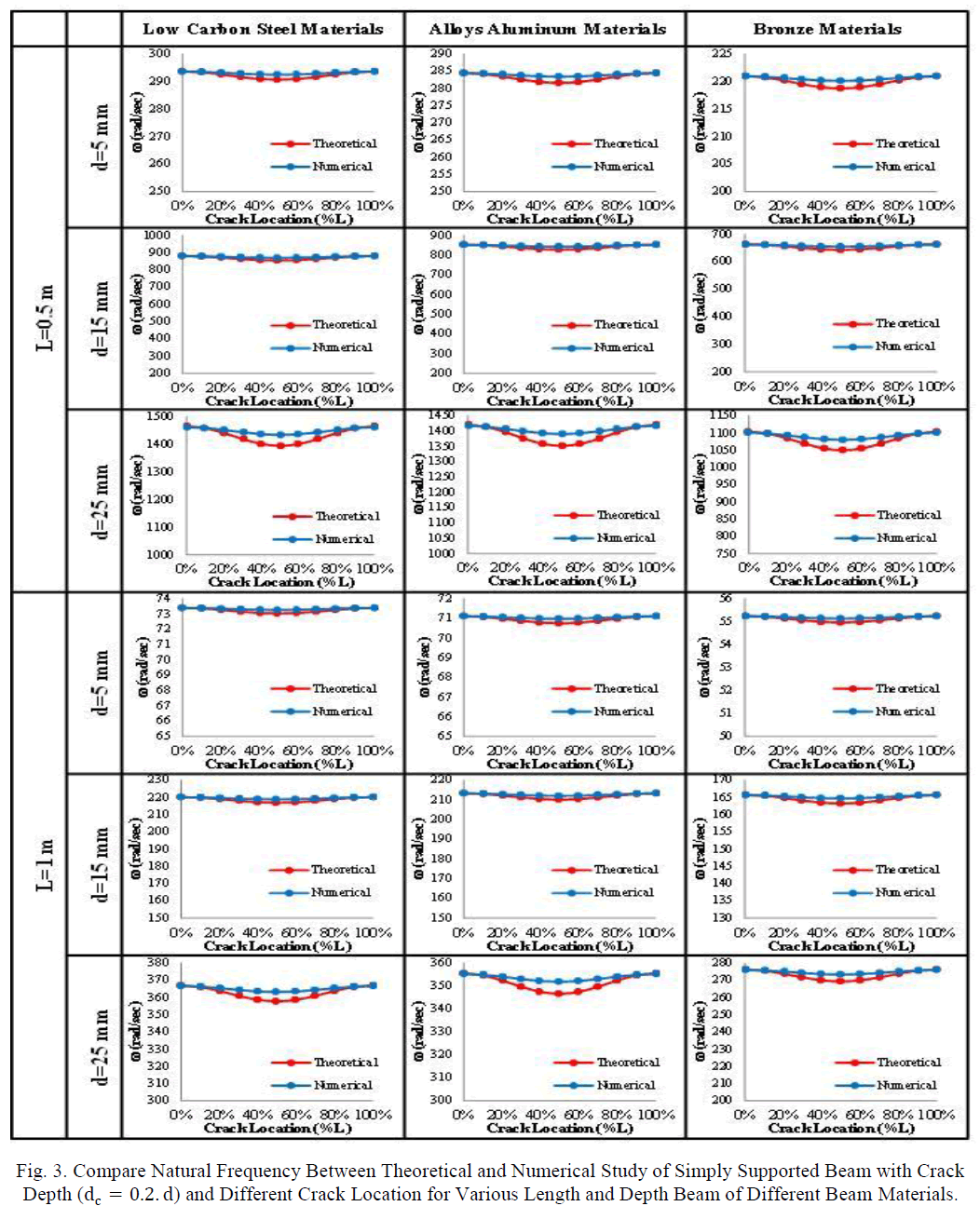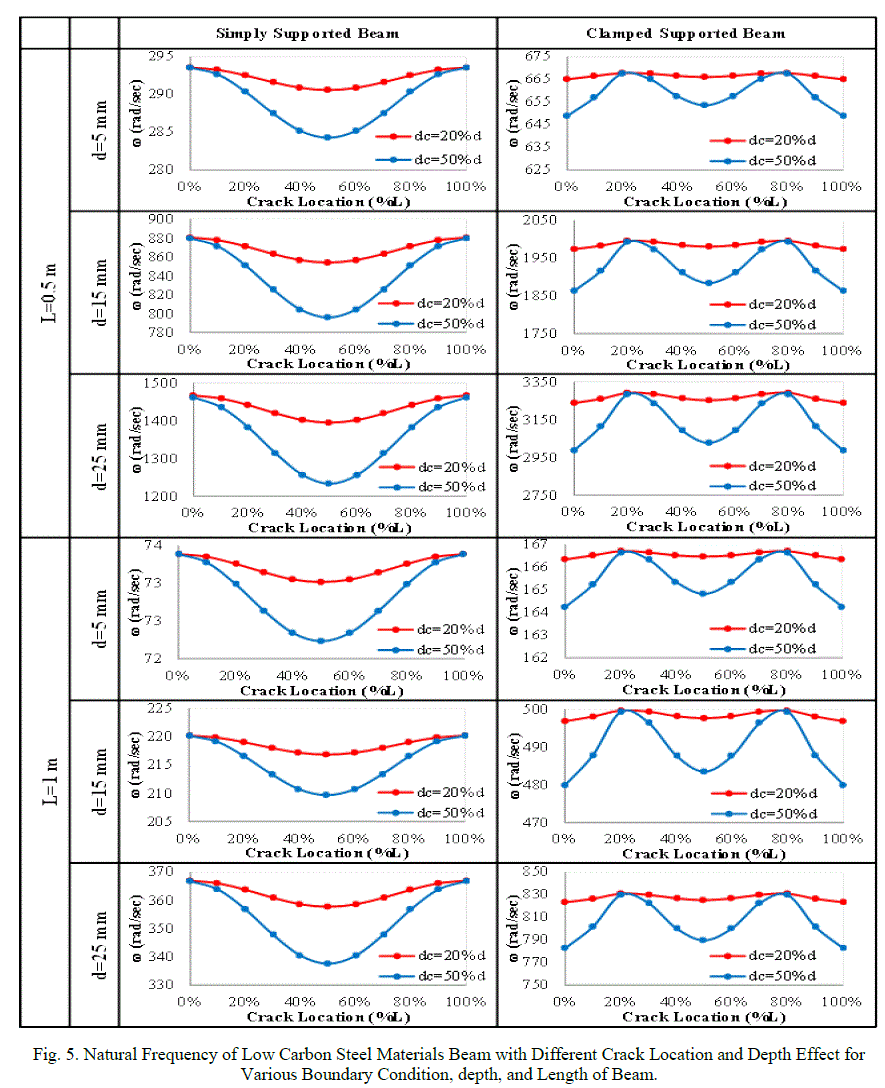V. CONCLUSION

The following concluding marks have been observed:

1. The analytical solution is a powerful tool for solving the differential equation for beam vibration with and without crack effect.

2. A comparison made between analytical results from solution of general equation of motion of beam with crack effect with numerical results by finite elements method shows a good approximation.

3. The crack causes, as expected, a decrease in the natural frequencies of flexural vibrations of the beam.

4. The crack in the beam has an effect on the stiffness of the beam, this will affect the frequency of the beam. So, with increasing of the crack depth the stiffness of beam will decreased, this will cause a decreasing the natural frequency of the beam.

5. The position of crack in the beam near the middle of the beam has more effect on the stiffness and natural frequency of beam from the other positions (near to the ends of the beam), i.e. frequency of beam when the crack in the middle position it has a lower frequency of beam with respect to the cracks near to the end position.

References

M. I. Friswell and J. E. T. Penny ‘Crack Modeling for Structural Health Monitoring’ Structural HealthMonitoring, Vol. 1, No. 2, pp. 139-148, 2002.
Singiresu S. Rao ‘Mechanical Vibration’ Addison-Wesley Publishing Book Company, 2000.
K. El Bikri, R. Benamar, and M.M. Bennouna ‘Geometrically non-linear free vibrations of clamped–clamped beams with an edge crack’ Computers and Structures, Vol. 84, pp. 485–502, 2006.
M. Al_Waily " Investigation of Health Monitoring of Composite Plate Structures-Using Vibration Analysis" Ph.D. Thesis Submitted to the Mechanical Engineering Department, College of Engineering, Alnahrain University, 2012.
D. Sreekanth Kumar, D. Roy Mahapatra, and S. Gopalakrishnan ‘A spectral !nite element for wave propagation and structural diagnostic analysis of composite beam with transverse crack’ Finite Elements in Analysis and Design, Vol. 40, 2004.
Ertugrul Cam, Sadettin Orhan, and Murat Luy ‘An analysis of cracked beam structure using impact echo method’ NDT&E International, Vol. 38, 2005.
H. R. Oz and M. T. Das ‘In-Plane Vibrations of Circular Curved Beams With a Transverse Open Crack’ Mathematical and Computational Applications, Vol. 11, No. 1, 2006.
Liao-Liang Ke, Jie Yang, Sritawat Kitipornchai ‘Postbuckling analysis of edge cracked functionally graded Timoshenko beams under end shortening’ Composite Structures, Vol. 90, 2009.
Luay S. Al-Ansari, Muhannad Al-Waily, and Ali M. H.Yusif Al-Hajjar ‘Experimental and Numerical Study of Crack Effect on Frequency of Simple Supported Beam’ Al-Khwarizmi Engineering Journal, Vol. 8, No. 2, 2012.
Hiroyuki Okamura, H. W. Liu and Chorng-Shin Chu ‘A Cracked Column Under Compression’ Engineering Fracture Mechanics, Vol. 1, 1969.
M.G.D. Geers, R. de Borst, and R.H.J. Peerlings ‘Damage and crack modeling in single-edge and double-edge notched concrete beams’ Engineering Fracture Mechanics, Vol. 65, 2000.
Mo-How H. Shen ‘Natural Modes of Bernoulli-Euler Beams With A Single-Edge Crack’ American Institute of Aeronautics and Astronautics, AIAA, 1990.
Murat Kisa ‘Free vibration analysis of a cantilever composite beam with multiple cracks’ Composites Science and Technology, Vol. 64, 2004.
Saber El Arem and Habibou Maitournam ‘A cracked beam finite element for rotating shaft dynamics and stability analysis’ Journal of Mechanics of Materials and Structures, Vol. 3, No. 5, 2008.
T.G. Chondros, A.D. Dimarogonas, and J. Yao ‘Longitudinal vibration of a bar with a breathing crack’ Engineering Fracture Mechanics, Vol. 61, 1998.
T.G. Chondros, A.D. Dimarogonas, and J. Yao ‘Vibration of A Beam with a Breathing Crack’ Journal of Sound and Vibration, Vol. 239, No. 1, 2001.
T.T. Lu, H.Y. Hu, and Z.C. Li ‘Highly accurate solutions of Motz’s and the cracked beam problems’ Engineering Analysis with Boundary Elements, Vol. 28, 2004.
H. Anton, Irl Bivens, and Stephen Davis 'Calculus' Anton Textbooks, Inc, Seventh Edition, (2002).
A. Jeffrey 'Advanced Engineering Mathematics' Harcourt / Academic Press, 2002.
E. J. Hearn ‘Mechanics of Materials-1 An Introduction to the Mechanics of Elastic and Plastic Deformation of Solids and Structural Materials, Third Edition’ E. J. Hearn, 1997.