ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
K. Thirumurugan 1, R. Vasanthakumari 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The problem of convection of compressible walters‟B′ viscoelastic fluid in a Darcy – Brinkman porous medium with effect of dusty particles is considered . By applying normal mode analysis method, the dispersion relation has been derived and solved analytically. It has been found that the medium permeability, dusty particles, gravity field and viscoelasticity introduce oscillatory modes. For stationary convection, it is found that the Darcy number has stabilizing effect whereas the dusty particles and medium permeability has destabilizing effects on the system. The effect of dusty particles, Darcy number and medium permeability have also been shown graphically.
Keywords |
| WaltersâÃâ¬ÃŸB′ fluid, Compressibility, Brinkman porous medium, Dusty particles, viscoelasticity. |
INTRODUCTION |
| In recent years, considerable interest has been evinced in the study of thermal instability in a porous medium because it has various applications in geophysics, food processing and nuclear reactor Rana[6]. A detailed account of the thermal instability of a Newtonian fluid under varying assumptions of hydrodynamics and hydromagnetics has been given by Chandrasekhar [1]. Lapwood[4] has studied the connective flow in porous medium using linearized stability theory. The Rayleigh instability of a thermal boundary layer in flow through a porous medium has been considered by Wooding[15]. Scanlon and Segel[10] have considered the effect of suspended particles on the onset of Be „nard and found that the critical Rayleigh number was reduced solely because the heat capacity of pure gas was supplemented by the particles. Sharma and Sunil [11] have studied the thermal instability of an Oldroydian viscoelastic fluid with suspended particles in hydromagnetics in a porous medium. There are many elastico – viscous fluids that cannot be characterized by MaxwellâÃâ¬ÃŸs constitutive relations or OldroydâÃâ¬ÃŸs constitutive relations. One such class of elastic – viscous fluid in Rivlin – Erickson fluid. Rivlin and Erickson [9] have proposed a theoretical model for such another elastico – viscous fluid. |
| The investigation in porous media has been started with the simple Darcy model and gradually was extended to Darcy – Brinkman model. A good account of convection problem in a porous medium is given by vafai and Hadim [14], Ingham and pop [2] and Nield and Bejan [5]. Kuzentsov and Nield [5] have studied the thermal instability of porous medium. Sharma et al.[12] have studied the instability of streaming Rivlin-Erickson fluids in porous medium. Recently, Rana and Thakur[8] studied the instability of couple – stress fluid permeated with suspended particles saturating a porous medium. Rana et al[7] have studied an effect of rotation on thermal instability of compressible WaltersâÃâ¬ÃŸB′ elastico – viscous fluid in porous medium. Shivakumara et al[13] has studied an effect of thermal modulation on the onset of thermal convection in WaltersâÃâ¬ÃŸB′ viscoelastic fluid in a porous medium. The interest of investigations of non – Newtonian fluids is also motivated by a wide range of engineering application which includes ground pollutions by chemicals which were non – Newtonian like lubricants and polymers in the treatment of sewage sludge in drying beds. Recently, polymers are used in agriculture, communications applications and in bio medical applications. Examples of these application filtration processes, packed bed reactors, insulation system, ceramic processing, enhanced oil recovery, chromatography etc. |
| Keeping mind the importance in various applications mentioned above, the objective of the present paper is to study the effect of suspended particles on thermal convection in WaltersâÃâ¬ÃŸB′ elastico – viscous fluid in a brinkman porous medium. This necessitates of additional parameter namely Darcy number. |
II. MATHEMATICAL MODEL AND PERTURBATION EQUATIONS |
| Consider an infinite, horizontal, compressible WaltersâÃâ¬ÃŸ B′ elastic – viscous fluid layer fluid layer of thickness d, heated and soluted from below so that the temperatures and densities at the bottom surface z = 0 are T0 and ρ0 and at the upper surface z = 0 are Td and ρd, respectively, and that a uniform temperature gradient β(= |dT/dz|) is maintained. The gravity field g(0,0,-g), and a uniform vertical magnetic field H(0,0,H), act on the system. |
 |
| The presence of particles adds an extra force term proportional to the velocity difference between particles and fluid and appears in the equation of motion(Eq.(1)). Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite sign, in the equation of the motion for the particles (Eq.(6)). The buoyancy force on the particle is neglected. Inter particles reactions are not considered either since the distance between the particles is quite large compared with their diameters. These assumptions have been used in writing the equation of motion (Eq.(6)) for the particles. The initial state of the system is taken to be quiescent layer(no settling) with a uniform particle distribution number. The initial state is defined as Eq.(7). |
 |
III. THE DISPERSION RELATION |
| Following the normal mode analyses, we assume that the perturbation quantities have x and y and t dependence of the form |
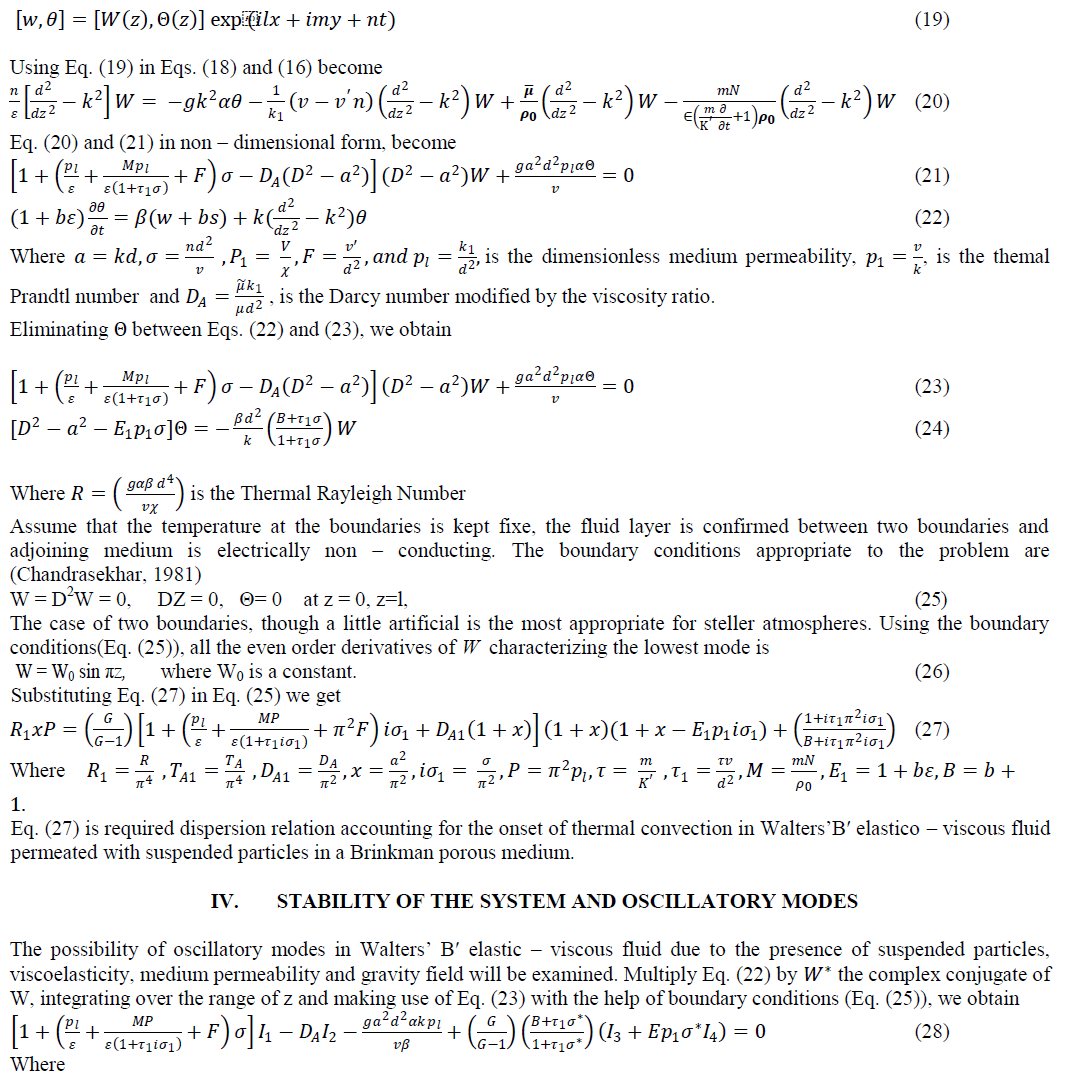 |
 |
 |
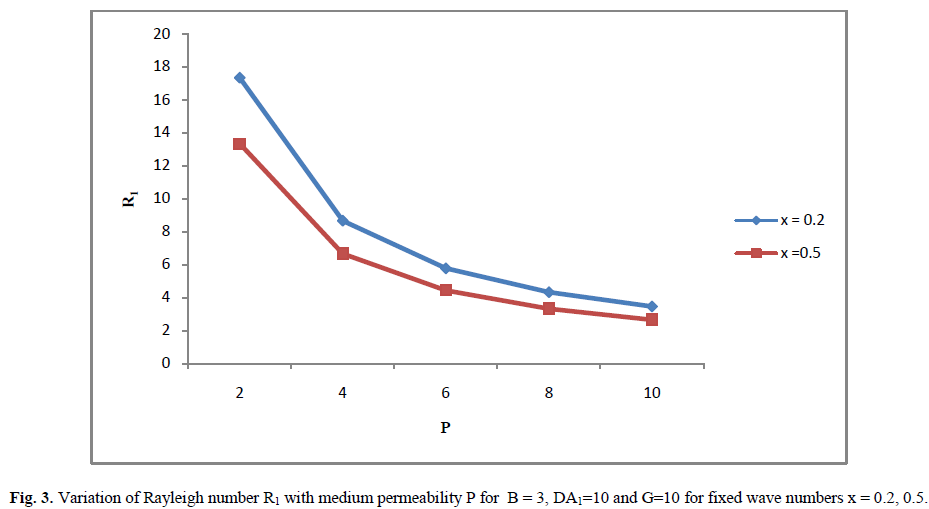 |
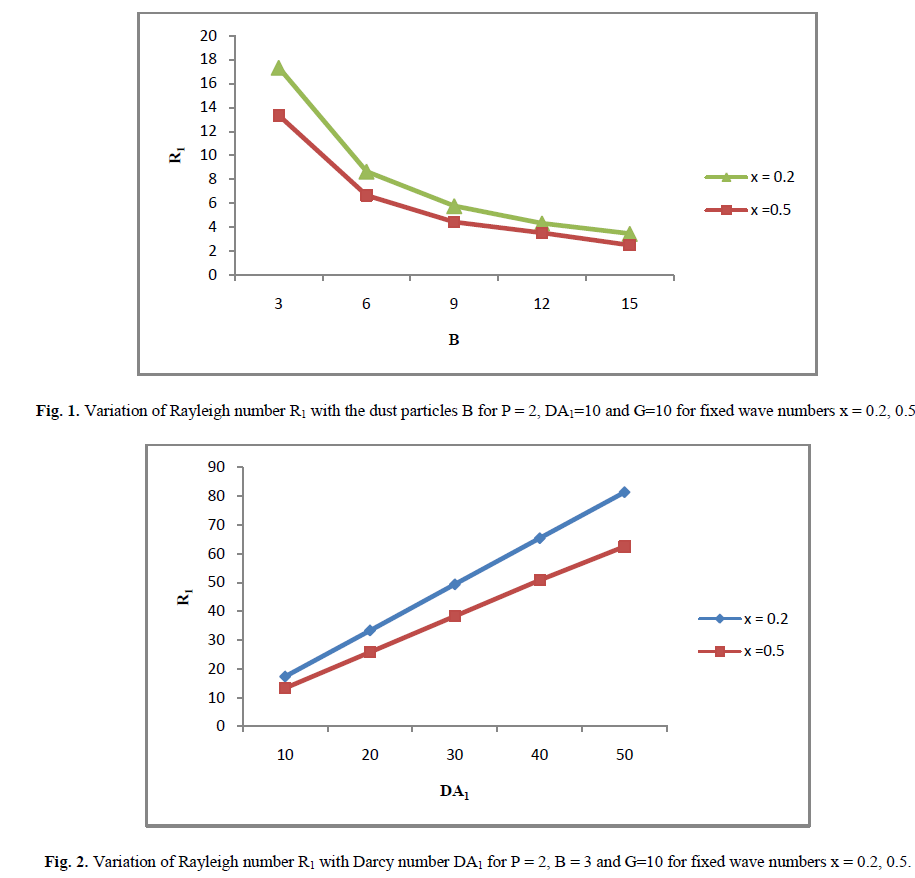
| The dispersion relation in Eq. (30) is analysed numerically to depict the stability characteristics. In Fig. (1), Rayleigh Number ïÿýïÿý1 is plotted against suspended particles B for P = 2 and ïÿýïÿýïÿýïÿý1 = 10 for fixed wave numbers ïÿýïÿý = 0.2, ïÿýïÿý = 0.5. This shows that suspended particles has destabilizing effect on thermal instability of WaltersâÃâ¬ÃŸB′ fluid in the Brinkman porous medium for fixed wave numbers ïÿýïÿý = 0.2, ïÿýïÿý = 0.5. Which clearly verifies the result numerically as derived in Eq. (31). In Fig. (2), Rayleigh Number R1 is plotted against with Darcy Number has a stabilizing effect on thermal convection in WaltersâÃâ¬ÃŸB′ elastico viscous fluid permeated with dusty particles in a Brinkman porous medium which is clearly verifies the result numerically as derived in Equation (32). In Fig (3) Rayleigh number R1 is plotted against medium permeability P for ïÿýïÿýïÿýïÿý1 = 10 and B = 3 for fixed wave numbers ïÿýïÿý = 0.2, ïÿýïÿý = 0.5 . This slows that medium permeability has a destabilizing effect on the thermal convection in WaltersâÃâ¬ÃŸB′ elastico-viscous fluid permeated with suspended particles in a Brinkman porous medium which is clearly verifies the result numerically as derived in Eq. (33). |
VI. CONCLUSION |
| The effect of suspended particles on thermal convection in WaltersâÃâ¬ÃŸB′ elastico-viscous fluid heated from below in the Brinkman porous medium has been investigated. The dispersion relation, including the effects of dusty particles, Darcy number, medium permeability and viscoelasticity on the thermal convection in WaltersâÃâ¬ÃŸB′ fluid in porous medium is derived. From the analysis, the main conclusions are as follows: |
 |
| (iii) The effects of dusty particles, Darcy Number and medium permeability on thermal convection in WaltersâÃâ¬ÃŸB′ elastico – viscous fluid permeated with dusty particles, in a Brinkman porous medium have been shown analyzed. |
| (iv) The oscillatory modes introduced due to the presence of viscoelasticity, dusty particles, gravity field and medium permeability, which were non – existent in their absence. |
References |
|