ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Mohinder Pal, Palvee and Kamaljeet Kaur Department of Electronics &Communication Engineering, IITT Engineering College, Pojewal, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Many different power frequencies were used in the 19th century. Very early isolated AC generating schemes used arbitrary frequencies based on convenience for steam engine, water turbine and electrical generator design. Frequencies between 16⅔ Hz and 133⅓ Hz were used on different systems. In this paper frequency deviation problem associated with load frequency control is evaluated. It is seen that Integral Controller is required to stable the frequency by properly selecting control parameters of the dual mode controller. The primary reason for accurate frequency control is to allow the flow of alternating current power from multiple generators through the network to be controlled. The trend in system frequency is a measure of mismatch between demand and generation, and so is a necessary parameter for load control in interconnected systems.
Keywords |
| Regulating system, Steady-state response, Dynamic response. |
INTRODUCTION |
| Electric power is generated by converting mechanical energy into electrical energy. The rotor mass, which contains turbine and generator units, stores kinetic energy due to its rotation. This stored kinetic energy accounts for sudden increase in the load. Let us denote the mechanical torque input by Tm and the output electrical torque by Te. Neglecting the rotational losses, a generator unit is said to be operating in the steady state at a constant speed when the difference between these two elements of torque is zero. In this case we say that the accelerating torque is zero. |
| Ta=Tm-Te |
| When the electric power demand increases suddenly, the electric torque increases. However, without any feedback mechanism to alter the mechanical torque, Tm remains constant. Therefore the accelerating torque given by becomes negative causing a deceleration of the rotor mass. As the rotor decelerates, kinetic energy is released to supply the increase in the load. Also note that during this time, the system frequency, which is proportional to the rotor speed, also decreases. We can thus infer that any deviation in the frequency for its nominal value of 50 or 60 Hz is indicative of the imbalance between Tm and Te. The frequency drops when Tm < Te and rises when Tm > Te. |
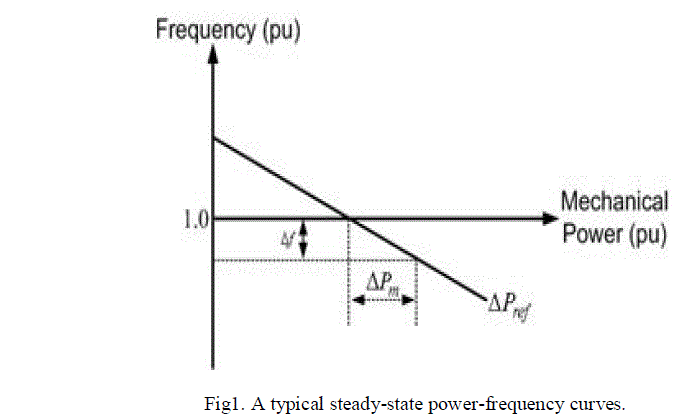
| The steady state power-frequency relation is shown in Fig.1. In this figure the slope of the ΔPref line is negative and is given by |
| -R=Δf / Δ Pm |
| Where R is called the regulating constant |
| In [1], dynamic characteristics of frequency oscillation after a disturbance based on measurement analysed. In this work author firstly observed the frequency oscillation sat each point and phase differences among them, global behaviours of the power system are also investigated. It is considered that power flow varied in the power system just after the disturbance. Secondly, transient behaviours are studied in detail through the Wavelet analysis. Some interesting interactions among the local power systems can be observed and system performances originated from a Load Frequency Control (LFC) can be extracted. Finally, frequency variation characteristics by the LFC. |
 |
| are studied on a plane of frequency deviation versus phase difference. Then the stiffness and controlled behaviours of the power system are carefully considered. |
| In [2] , author presented a new approach to study the area load frequency control (LFC) problem using fuzzy gain scheduling of proportional-integral (PI) controllers. The control scheme adopts a formulation for the area control error which always guarantees zero steady state time error and inadvertent interchange. |
| In [3], Load-frequency control service in a deregulated environment is discussed. The method assumes that load frequency control is performed by an ISO based on parameters defined by the participating generating units. The participating units comprise utility generators and independent power producers. The utilities define the units, which will be under load-frequency control, while the independent power producers may or may not participate in the load frequency control. For all the units, which participate in the load-frequency control, the generator owner defines a generation limits, b rate of change and c economic participation factor. This information is transmitted to the ISO. This scheme allows the utilities to economically dispatch their own system, while at the same time permit the ISO to control the interconnected system operation. |
PRESENT WORK |
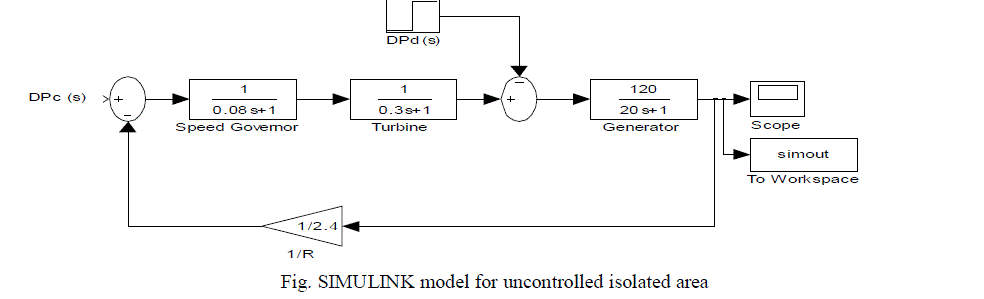
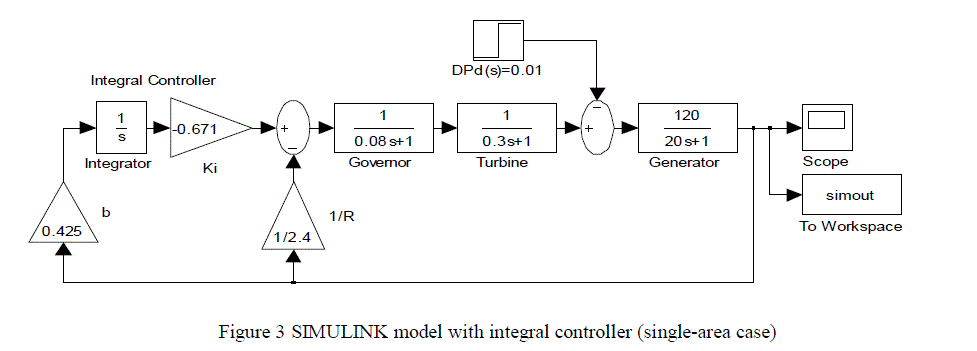
| A SIMULINK model is constructed for isolated uncontrolled power system as shown in Figure 2. SIMULINK model with integral controller (single-area case) shown in Figure 3. |
 |
 |
 |
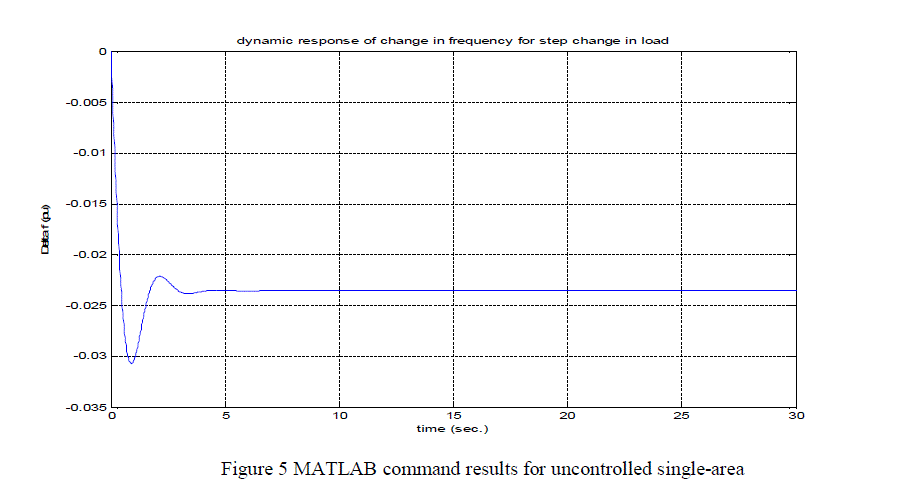 |
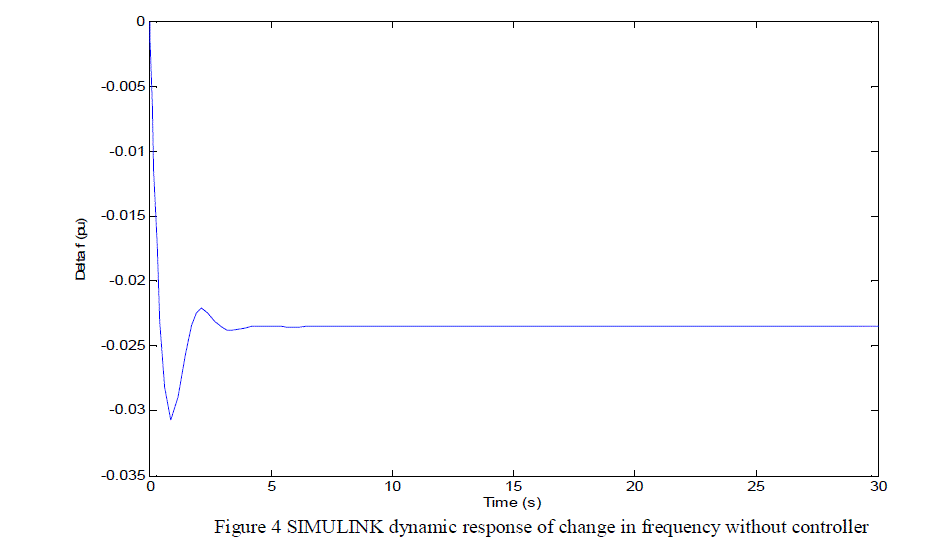
| We observed that the both responses match with each other, also the steady-state frequency deviation Δf (steady state) is zero and frequency returns to its steady value in approximately 6 seconds. |
CONCLUSION |
| In this paper, the above results depicts that we can stabilize the frequency by using integral controller. It is seen that Integral Controller results a stable frequency. With the proper choice of control parameters of the dual mode controller, frequency deviations and the tie line power can be effectively controlled. Due to disturbances in the power system, the frequency is deviates. So Integral Controller is used to overcome this problem. By using the Integral Controller frequency can be stable. Load-frequency control in a deregulated environment may result in free choice by units to participator not in this operation. |
References |
|