ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Deepak Gupta, Payal Singla, Shashi Bala
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Flow shop scheduling problems as a typical manufacturing challenge have gained wide attention in academic fields. In this paper, we consider two stage flow shop scheduling problem in which a job block for a group job and the interval of non-availability of machine has been taken with an objective to minimize the make span. This paper provides a branch and bound technique to find optimal or near optimal sequence. This approach is very simple and easy to understand and, also provide an important tool for decision makers to design a schedule for two stage flowshop scheduling problems. The method is clarified with the help of numerical illustration.
Keywords |
| Flow shop scheduling, Flow Time, Make span, Branch and Bound Technique. |
INTRODUCTION |
| A flow shop is characterized by unidirectional flow of work with a variety of jobs being processed sequentially in a one-pass manner. The processing time of all the jobs are assumed to be known and all the jobs are processed in the same order in various machines. Scheduling in a manufacturing system is necessary to maintain efficiency, productivity and quality of production. The study of scheduling problem has attracted researchers from various fields. This is due to the increased awareness of management to the potential gains realizable when good scheduling algorithms are employed. The majority of academic research on scheduling has centred on the sequencing problems. The sequencing problem is considered with determining the sequence in which a set of jobs is to be performed by each of the machine. Good scheduling is necessary to maintain system efficiency and control of operation. In scheduling literature, there are several scenarios of handling non-availability intervals. Lee[8] calls the scheduling model resumable, if the job can be continued after the interval without any penalty; the model is called nonresumable, if an interrupted job must restart after the interval from scratch, and according to the semi-resumable model the job will have to be partially restart. The problem studied in this paper corresponds to the resumable model with branch and bound method. Branch and bound is an exact method usually used in scheduling problems to find optimal solutions. This method requires three components: a lower bound (LB), an upper bound and a branching strategy. Branch and bound provides a systematic enumeration procedure that considers bounds on the objective function for different subsets of solutions. Subsets are eliminated when their lower bound is dominated by the bound of other subset. The procedure is repeated until the search tree is exhausted and the optimal solution is found. |
LITERATURE REVIEW |
| Johnson[6] has proposed a basic algorithm for n jobs, two-machine scheduling problem with minimizing makespan. The work was extended by Ignall and Scharge[5],Lomnicki[9], Yoshida and Hitomi[15],Maggu and Das[10], Nawaz et al.[11] , Sarin and Lefoka[12] , Koulamas[7], Heydari[4] ,Temiz and Erol[14]etc. by considering various parameters. Yoshida and Hitomi[15] considered two stage flow shop problem to minimize the makespan whenever set up times are separated from processing time. The basic concept of equivalent job for a job block has been introduced by Maggu and Dass[10]. Heydari[4] dealt with a flow shop scheduling problem where n jobs are processed in two disjoint job blocks in a string consists of one job block in which order of jobs is fixed and other job block in which order of jobs is arbitrary. Singh T.P. and Gupta Deepak[13] studied the optimal two stage production schedule in which processing time and set up time both were associated with probabilities including job block criteria. |
| Lomnicki [9]introduced the concept of flow shop scheduling with the help of branch and bound method. Further the work was developed by Chandrasekharan[2] , Brown and Lomnicki[1], with the branch and bound technique to the machine scheduling problem by introducing different parameters. In many practical scheduling applications it is required to consider the situation in which the processing machines are not continuously available throughout the planning period. This happens when maintenance requirements, rest periods or machine breakdowns have to be taken into account. In this paper we have extended the study made by Gupta D. et al. [3] by considering the breakdown intervals on each machine. Hence the problem discussed here is wider and has significant use of theoretical results in process industries. |
PRACTICAL SITUATION |
| Many applied and experimental situation occur in our day to day working in factories and industrial concern when the machines are not continuously available due to electric current, breakage of machine etc. We have to consider the nonresumable model. The practical situation may be taken in a production industry; manufacturing industry etc. |
| Assumptions: |
| 1. All the jobs are available for processing at time zero. |
| 2. Each job must be completed when started. |
| 3. To make job on a second machine, it must be completed on the first machine. |
| 4. Machines may be idle. |
| 5. Setup Times are known and are included in processing times. |
| 6. Machines can break down throughout the scheduling period. |
| Terminology : |
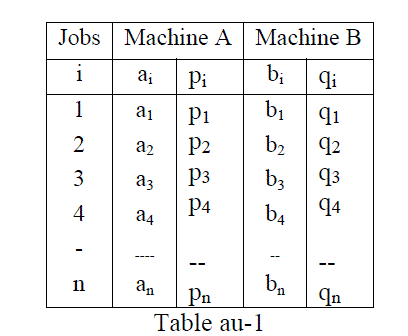
| We are given n jobs to be processed on two stage flowshop scheduling problem and we have used the following notations: |
 |
| machine A &B |
MATHEMATICAL DEVELOPMENT |
| Consider n jobs say i=1, 2, 3 … n are processed on two machines A & B in the order AB. A job i (i=1,2,3…n) has processing time ai & bi on each machine respectively, assuming their respective probabilities pi , qi such that 0 ≤ pi ≤ 1, Σpi = 1, 0 ≤ qi ≤ 1, Σqi = 1. Let an equivalent job β is defined as (k, m) where k, m are any jobs among the given n jobs such that k occurs before job m in the order of job block (k , m) and the machines are not available in the interval (sj, tj).The mathematical model of the problem in matrix form can be stated as : |
 |
| Our objective is to obtain the optimal schedule of all jobs which minimize the total elapsed time whenever the machines are not available in the given interval and job block for a group job is being considered, using branch and bound technique. |
Algorithm: |
| Step1: Calculate expected processing time on machines A anb B respectively as follows: |
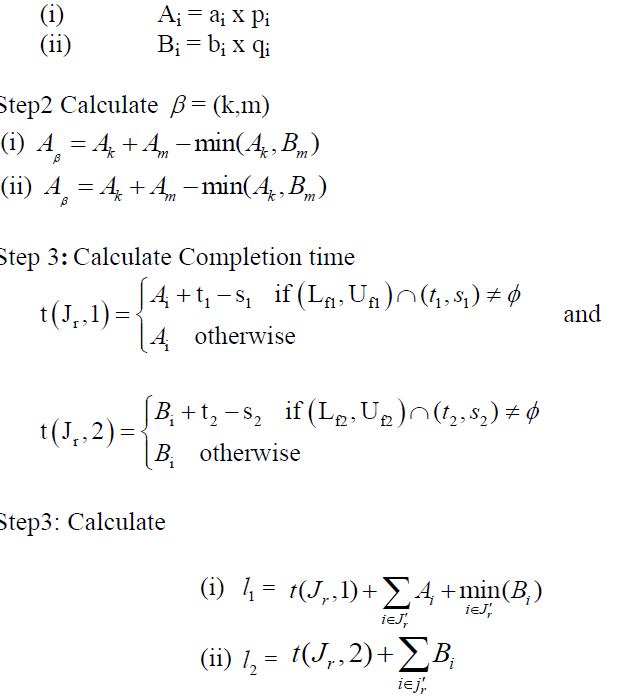 |
| Step 4: Calculate |
| l = max [ 1 l , 2 l ] |
| We evaluate l first for the n classes of permutations, i.e. for these starting with 1, 2, 3………n respectively, having labelled the appropriate vertices of the scheduling tree by these values. |
| Step 5: Now explore the vertex with lowest label. Evaluate l for the (n-1) subclasses starting with this vertex and again concentrate on the lowest label vertex. Continuing this way, until we reach at the end of the tree represented by two single permutations, for which we evaluate the total work duration. Thus we get the optimal schedule of the jobs. |
| Step 6: Prepare in-out table for the optimal sequence obtained in step 5. |
| Numerical Illustration: |
| Consider 5 jobs 2 machine flow shop problem whose processing time of the jobs on each machine is given. |
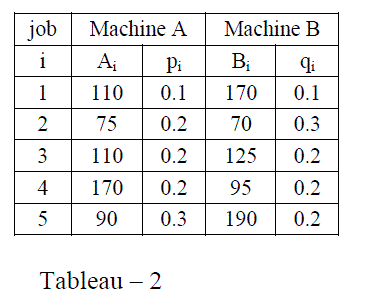 |
| Our objective is to obtain optimal schedule for above said problem in which jobs 2,5 are to be processed as a group job (2,5) and the intervals of unavailability of machines are (35,40) & (60-65) on machine A and on machine B respectively. |
| Solution: As per step1 the expected processing times for machines A and B are as follow: |
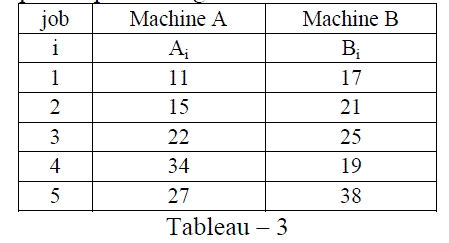 |
| As per step2 |
| Compute Aβ and Bβ when β =(2, 5) |
| As job block |
| (i) Aβ= 21 and (ii)Bβ= 38 |
| The reduced problem is given by |
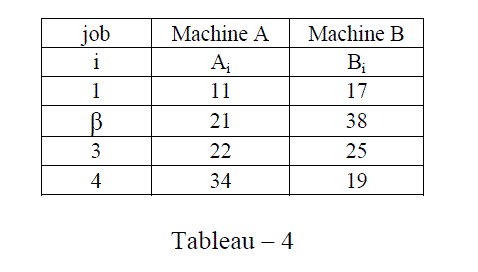 |
| As per Step3: Calculate Lower Bounds LB(Jr) |
| For J1 = (1).Then J′(1) = { β,3,4}, we get |
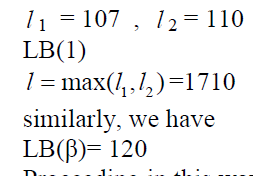 |
| Proceeding in this way, we obtain lower bound values as shown in the tableau- 5 |
 |
| The complete schedule tree is shown as in Figure 1 |
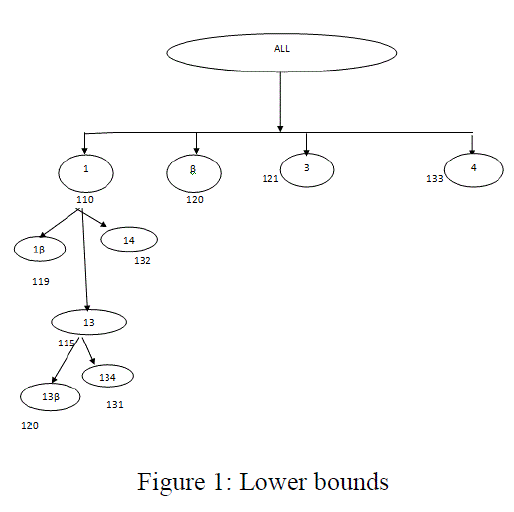 |
| As per Step 4 & 5 : |
| Therefore the sequence S1 is 1-3-β-4 i.e. 1-3-2- 5-4 and the corresponding in-out table on sequence S1 is as follows: |
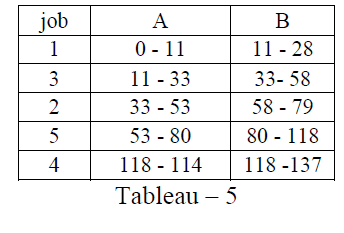 |
| Total Elapsed Time = 137 units. |
Remarks: |
| The study may further be extended by considering various parameters such as , weightage, Transportation Time etc. |
References |
|