ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Swarima Tewari1 and Soubhik Chakraborty2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The present paper gives a method of optimizing the performance of a music learner using the “Kmeans clustering” algorithm in data mining. It also shows how to prevent music piracy by hiding musical data by giving some unique codes to music files. An illustrative example is provided using a note sequence in a Hindustani raga, namely, Bhimpalashree.
Keywords |
| Data mining, K-means clustering algorithm, raga, melody, performance optimization, music piracy |
I. INTRODUCTION |
| A. PROBLEM IDENTIFICATION |
| How can a researcher help an artist to improve or optimize his or her performance without loosing the quality? This has always been a big question of perennial interest in music research. It is quite a challenge for a beginner or a music learner how to overcome the problem of repeating similar melodies while performing on stage. This is especially true in Indian classical music where it is expected that the artist would present the alankars (melodic embellishments) in an extempore fashion. |
| On the other hand, there is another problem that a large number of music files are available on various websites and anyone can easily download these musical data because there are no personalized services to hide this information. |
| In the present paper, both these problems are addressed using the “K-means clustering” algorithm in data mining. As it turns out, this algorithm can help in improvising the artist’s performance and saves time. Moreover, it can hide the musical information in the form of some unique codes. While doing the clustering, if k is properly given, the data in the list may be properly grouped and the grouped music can be used as the user's preference [2]. |
| B. DATA MINING IN MUSICOLOGY |
| Data mining is an important application of computer science that has increasing relevance in research in the humanities. Data mining techniques can enrich our understanding of music and music cognition. They allow for analysis on a scale that is not possible with the qualitative analytical methods [3]. |
| C. K-MEANS CLUSTERING |
| It is an iterative clustering algorithm in which items are moved among sets of clusters until the desired set is reached. The cluster mean of Ki = {ti1, ti2 ….., tij} is defined as |
 |
| D. MELODY ANALYSIS |
| Melody may be mathematically defined as a sequence of notes “complete” in some sense as determined by music theory, taken from a musical piece (Chakraborty et. al. [1]). A melody need not be a complete musical sentence. It suffices if it is a complete musical phrase. A Segment is a sequence of notes which is a subset of melody but is itself incomplete. For example, {Ma, Pa, Komal Ni, Sa} is a melody being a complete musical phrase in the Hindustani raga Bhimpalashree being analyzed here but {Ma, Pa} is its sequential subset and hence a segment in this raga. Here a raga, which is the nucleus of Indian classical music, is a melodic structure with fixed notes and a set of rules characterizing a certain mood conveyed by performance. Length of a melody or its segment refers to the number of notes in it. Significance of a melody or its segment (in monophonic music such as Indian classical music) is defined as the product of the length of the melody and the number of times it occurs in the musical piece. Thus both frequency and length are important factors to assess the significance of a melody or its segment. For a more technical definition of significance of melody in polyphonic music, see Adiloglu, Noll and Obermayer [5]. |
| Musical data being chronological, the numbers representing pitches in different octaves will be the possible response entry corresponding to the argument time which would in our case be just the instance (1, 2, 3…) at which a musical note is realized. The tonic Sa is taken at the note natural C (i.e. the scale is C). Also, C of the middle octave is assigned the number 0 representing its pitch as the reference point for other notes of higher and lower pitch to be assigned numbers accordingly as 1, 2, 3…. or -1, -2, -3…respectively (detailed in table 1). This is the technique that is used for structure analysis and we are motivated by the works of Adiloglu, Noll and Obermayer [5]. Our database for analysis comprises of a sequence of notes of the song based on raga Bhimpalashree. This is given in table 4 in Appendix. |
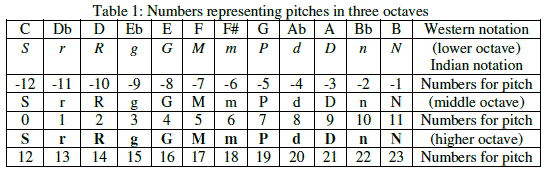 |
| Abbreviations: The letters S, R, G, M, P, D and N stand for Sa, Sudh Re, Sudh Ga, Sudh Ma, Pa, Sudh Dha and Sudh Ni respectively. The letters r, g, m, d, n represent Komal Re, Komal Ga, Tibra Ma, Komal Dha and Komal Ni respectively. Normal type indicates the note belongs to middle octave; italics implies that the note belongs to the octave just lower than the middle octave while a bold type indicates it belongs to the octave just higher than the middle octave. Sa, the tonic in Indian music, is taken at C. Corresponding Western notation is also provided. The terms “Sudh”, “Komal” and “Tibra” imply, respectively, natural, flat and sharp. |
| Musical features of raga Bhimpalashree |
| Thaat( a method of grouping ragas according to scale): Kafi |
| Aroh (ascent): n S g M, P, n, S Awaroh (descent): S n D P M g R S |
| Jati: Aurabh-Sampoorna (five distinct notes allowed in ascent; seven in descent) |
| Vadi Swar (most important note): M Samvadi Swar (second most important note): S |
| Prakriti (nature): restful Pakad (catch): n S M, Mg, PM, g, M g R S |
| Stay notes (nyas swars): g M P n Time of rendition: 1PM-3 PM |
| Table 2 gives the melodic phrases and segments (built with the help of table 4 given in appendix) |
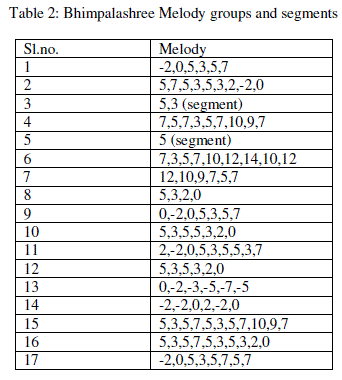 |
| Remark: A melodic phrase should have at least three notes. If less, it can only be a segment.The other property of being complete in order to be taken as a sigle entity and hence qualify to be a melody we have already discussed earlier. |
II. EMPIRICAL RESULTS |
| In order to assign a unique code to a melody, each note in a melody group is multiplied to its position number and added. We should be careful that each and every value must be unique. Code calculation for melody groups:- |
| Melody group/segment no.1. -2, 0, 5, 3, 5, 7 |
| = (1×-2)+(2×0)+(3×5)+(4×3)+(5×5)+(6×7) |
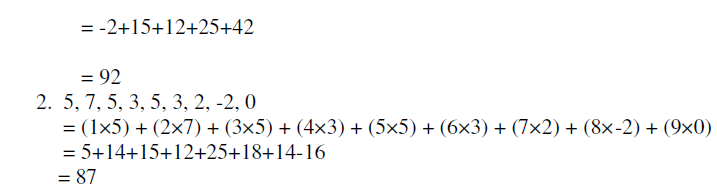 |
| Proceeding in this manner, after calculating for every melody group, we finally get: |
| 92, 87, 11, 322, 5, 464, 154, 17, 110, 73, 185, 48, -98, -8, 452, 174, 90 |
| 1. Take two means say K1=92, K2=87 and divide all the values in 2 groups, G1 and G2 by assigning each object to the group that has the closest mean. |
| 2. When all objects have been assigned, recalculate the positions of the K mean |
| 3. Now repeat it until the centroids no longer move. |
| Our results are summarised in table 3. |
 |
| In the 2nd step we take the means of 1st G1 and G2 and then assign the values to both the groups which are closer to 227 and 16.8750 and so on. Finally we can see that at the 2nd and 3rd steps, groups are repeating. At this point, we stop further calculation. |
III. CONCLUSION |
| We conclude that at steps 2 and 3, groups are repeating themselves; that is to say, melodies are repeating. If performance is falling in the same groups repeatedly the performer can optimize his performance by avoiding the repetition of melodies again and again. It saves the time and increases newness and generates interest in the listeners. |
| At the same time, by assigning unique codes to each melody group, we have personalized musical data which tackles the other problem of music piracy as our strategy can be easily extended to hide music files. |
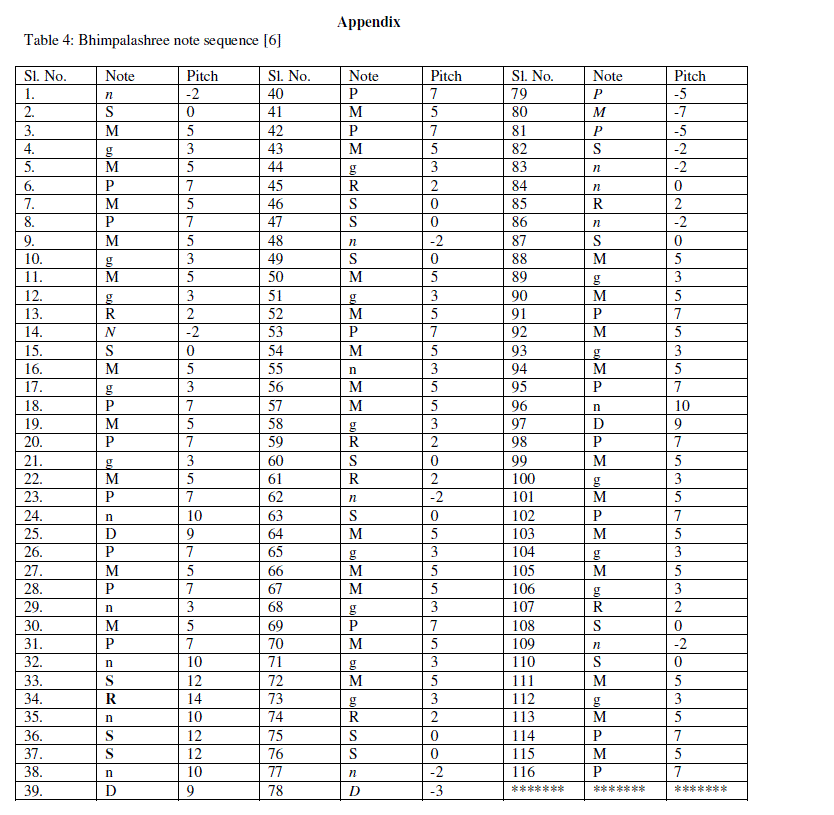 |
References |
|