ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Binit Amin1, Patel Amrutbhai2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This work informs a survey on vector quantization (VQ) based lossy image compression using wavelets. The objective of image compression is to help in storing the transmitted data in proficient way by decreasing its redundancy. It also involves reducing the size of image data file, while retaining necessary information and maintaining a certain level of quality. Depends on this the image compression is classified into two categories: lossy and lossless image compression. There are many lossy techniques exists for image compression in digital domain, among this wavelet transformation based image compression by using vector quantization (VQ) provides good picture quality and better image compression ratio compared to all other techniques. Vector quantization (VQ) has the potential to greatly reduce the amount of information required for an image because it compresses in vectors which provides better efficiency than compressing in scalars. The most popular algorithm for generating a Vector Quantizer codebook is the Linde-Buzo-Gray (LBG) algorithm or Generalised-Lloyd (GLA) algorithm. The objective is to generate the standard codebook by using some standard training set which is capable of successfully coding images outside of the training set. Vector quantization (VQ) based coded images then encoded for transmission by using different encoding technique like Huffman encoding, Run Length Encoding (RLE) etc.
Keywords |
| Vector quantization (VQ), Image compression, Codebook, Codevector, Encoding, Discrete wavelet transform (DWT). |
INTRODUCTION |
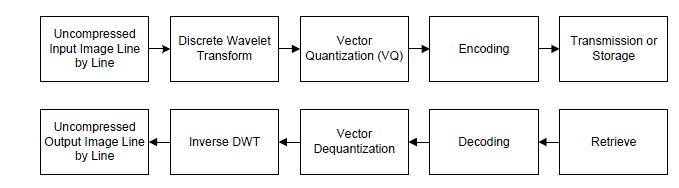
| As we know World Wide Web Applications have extensively grown since last few decades and it has become requisite tool for education, communication, industry, amusement etc. These applications are multimedia-based applications consisting of images and videos. Images/videos require enormous volume of data items, which need higher channel bandwidth for efficient transmission. But again to provide large bandwidth is an easy task. Further high degree of redundancies is observed in digital images. Thus the need for image compression arises for resourceful storage and transmission. In recent years, many studies have been made on wavelets. This paper presents an excellent overview of what wavelets have brought an application to the fields of image processing. A wavelet based image compression system can be created by selecting a type of quantizer, wavelet function and statistical coder. Initial steps in wavelet compression are to perform a discrete wavelet Transformation (DWT), quantization of the wavelet space image sub bands followed by encoding these sub bands. Wavelet images themselves are not compressed images; rather it is quantization and encoding stages that do the image compression. |
| Work of quantizer is to reduce the number of bits needed to store the transformed coefficients by reducing the precision of those values. Since this mapping technique is a many-to-one mapping itâÃâ¬ÃŸs a lossy process and is the main source of image compression in an encoder. Basically there are two types of quantizer: scalar quantization (SQ) and vector quantization (VQ). If the quantization is performed on a group of coefficients together then this is known as Vector Quantization (VQ). VQ is one of the method which has been widely used for data compression due to its theoretical advantages over the scalar quantization schemes. However, the computational complexity of both the codebook design and the vector lookup during the encoding phase is obviously a burden of its realization. Since the codebook can be pre-generated before the encoding process, the efficiency of the vector lookup is comparatively more significant. |
 |
| A Quantizer simply reduces the number of bits needed to store the transformed coefficients by reducing the precision of those values. Since this is a many-to-one mapping, itâÃâ¬ÃŸs a lossy process and is the main source of compression in an encoder. Basically there are two types of quantizer: scalar quantization (SQ) and vector quantization (VQ). If the quantization is performed on a group of coefficients together then this is known as Vector Quantization (VQ). VQ is one of the method which has been widely used for data compression due to its theoretical advantages over the scalar quantization schemes. However, the computational complexity of both the codebook design and the vector lookup during the encoding phase is obviously a burden of its realization. Since the codebook can be pre-generated before the encoding process, the efficiency of the vector lookup is comparatively more significant. |
| Entropy coding substitutes a sequence of codes for a sequence of symbols where, the codes are chosen to have fewer bits when the probability of occurrence of the corresponding symbol is higher. This process removes redundancy in the form of repeated bit patterns in the output of the Quantizer. The most commonly used entropy coders are the Huffman Coding, Arithmetic Coding, Run Length Encoding (RLE) and Lempel-Ziv (LZ) algorithm, although for applications requiring fast execution, simple Run Length (RLE) has proved very effective [3]. Consequently arithmetic codes are most commonly used in wavelet-based algorithms. |
| Finally image reconstruction, or decompression is achieved by carrying out the above steps in reverse and inverse order. Thus, to restore the original image the compressed image is decoded, de-quantized and then an inverse DWT is performed [5]. This paper is organized as follows. In sections II an introduction is given to the use of wavelet transform for image compression. In section III and IV, an introduction is given to the main ideas of Vector Quantization (VQ) algorithm and codebook generation respectively. Finally, future enhancement and the conclusion of the work are suggested. |
WAVELET TRANSFORM |
| Wavelet transform provides the time and frequency representation simultaneously. There are mainly two types of wavelet transforms, continuous wavelet transformation (CWT) and discrete wavelet transformation (DWT). Science my algorithm is to be based on DWT, so I will discuss the concept of DWT in this paper. With DWT we can decompose an image more than once. Mostly two ways for decomposition are used: Pyramidal decomposition and Packet decomposition. Discrete wavelet transform based on image compression adopts the fast algorithm for two dimension. The original image decomposes into four sub parts after passing the image into high pass filter and low pass filter. The four subbands are LL, HL, LH and HH respectively. LL is a low frequency sub-band of the approximate image. HL is a high frequency sub-band of the horizontal details of the image. LH is a high frequency sub-band of the vertical details of the image. HH is a high frequency sub-band of the diagonal details of the image [5]. |
| This process is called the first level of wavelet decomposition. The low frequency sub-band can be continually decomposed into four sub-bands. Theoretically the decomposition process can be infinitely repeated. So people must consider the quality of the reconstructed image. Thus people donâÃâ¬ÃŸt decompose image beyond fifth level decomposition. Researchers usually uses the third level of decomposition. The three level wavelet based decomposition model is shown in figure. |
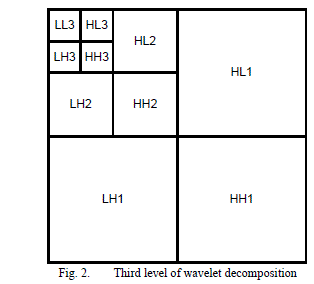 |
| After applying the wavelet transform we can create the original image back without losing the information. But the energy of whole image is redistributed after the transform. Low frequency sub-band image contains major information and high frequency sub-band values approximate to zero, the more high frequency the more obvious this situation. For images, the low frequency part is primary part which can represent the image information. So researchers take full advantage of the characteristic of wavelet transform and employ proper method to process the image coefficients for achieving effective compression. Figure shows the "Lena" image after one, two and three pyramidal decomposition steps. |
 |
| DWT can be used to reduce the image size without losing much of the resolution. For a given image, we can compute the DWT of each row and then discard all values in the DWT that are less than a certain threshold. We then save and transmit only those DWT coefficients that are above the threshold for each row and when we need to reconstruct the original image, we pad each row with as many zeros as the number of discarded coefficients are there and then by applying the inverse DWT to reconstruct each row of the original image. We also analyze that image at different frequency bands and reconstruct the original image, by using the coefficients that are of a particular related band [1 and 6]. |
| A. Algorithmic Steps: |
| The steps needed to compress an image are as follows: |
| Decompose the image into a sequence of wavelet coefficients „wâÃâ¬ÃŸ. |
| Use threshold function to modify the wavelet coefficients from „wâÃâ¬ÃŸ to another sequence „w'âÃâ¬ÃŸ. |
| Use vector quantization (VQ) to convert sequence „w'âÃâ¬ÃŸ into an index sequence „qâÃâ¬ÃŸ. |
| Apply entropy encoding to compress „qâÃâ¬ÃŸ into a sequence „eâÃâ¬ÃŸ. |
| In certain signals, many of the wavelet coefficients are close or equal to zero. Through a method called threshold, these coefficients may be modified so that sequence of the wavelet coefficients contains long strings of zeros. Then by using entropy encoding compression technique these long strings may be stored and sent electronically in much less space. There are different types of threshold. In hard threshold some tolerance is selected. Any wavelet whose absolute value falls below that selected tolerance is set to zero with the goal to introduce many zeros without losing the great amount of details. There isnâÃâ¬ÃŸt another straightforward way to choose the threshold value. Although the larger the threshold chosen the more error introduces into the process. The fourth step of the process known as vector quantization (VQ) converts a sequence of floating numbers „w'âÃâ¬ÃŸ to a sequence of integers „qâÃâ¬ÃŸ. The simplest form is to round the nearest integers. Another option is to multiply each number by a constant „kâÃâ¬ÃŸ, and then rounding it to the nearest integer. This quantization process is called Lossy because it introduces an error into the process, since the conversion of „w'âÃâ¬ÃŸ to „qâÃâ¬ÃŸ is many-to-one function. |
| Reconstruction of compressed image is done by the reverse process of the above compression process. But we cannot get exactly original image because of there is some error due to quantization and threshold. Though in DWT we achieve very high compression ratio by losing minimum amount of information and if we increases the levels then we get more compression ratio but the reconstructed image is not identical to the original image. MSE also increases if the level of DWT increases [8] |
VECTOR QUANTIZATION |
| The vector quantization is a classical quantization technique for signal processing and image compression which allows the modelling of probability density functions by the distribution of prototype vectors. Main use of vector quantization (VQ) is for data compression [2 and 3]. It works by dividing a large set of values (vectors) into groups having approximately the same number of points closest to them. Each group is represented by its centroid value, as in kmeans algorithm and some other algorithms. |
| The density matching property for vector quantization is powerful, especially in the case for identifying the density of large and high dimensioned data. Since data points are represented by their index to the closest centroid, commonly occurring data have less error and rare data have higher error. Hence VQ is suitable for lossy data compression. It can also be used for lossy data correction and density estimation. The methodology of vector quantization is based on the competitive learning paradigm, hence it is closely related to the self-organizing map model. Vector quantization (VQ) is used for lossy data compression, lossy data correction and density estimation. Finally image decompression, or reconstruction, is achieved by carrying out the above steps in reverse and inverse order. Thus, to restore the original image, the compressed image is decoded, de-quantized, and then an inverse DWT is performed. |
A. Principle of vector quantization |
| Vector Quantization assist to project a continuous input space on a discrete output space, while minimizing the loss of information. To define zones in the space, the set of points contained in each zone being projected on a representative vector |
| B. Vector quantization in image processing |
| The methodology used in vector quantization is also called "block quantization" or "pattern matching quantization" is often used in lossy image compression. |
 |
| It works by encoding values from a multidimensional vector space into a finite set of values from a discrete subspace of lower dimension. The lower-space vector requires less storage space, so the image can be easily compressed. Due to the density matching property of vector quantization, the compressed data have errors that are inversely proportional to their density. The renovation is usually done by projection or by using a codebook. In some cases, the codebook can also be used to entropy code the discrete value in the same step by generating a prefix coded variable-length encoded value as its output. The template is used to format your paper and style the text. All margins, column widths, line spaces, and text fonts are prescribed; please do not alter them. You may note peculiarities. For example, the head margin in this template measures proportionately more than is customary. This measurement and others are deliberate, using specifications that anticipate your paper as one part of the entire proceedings, and not as an independent document. Please do not revise any of the current designations. |
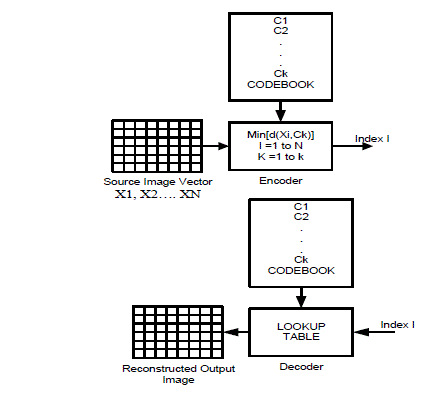
| The set of distinct amplitude levels are quantized jointly rather than each sample being quantized separately. Figure describes the basic block diagram of vector quantization. Consider N-dimensional vector [X1, X2…. XN] of different amplitude levels. It is compressed by choosing the nearest matching vector from a set of K-dimensional vectors [C1, C2…. CK]. All possible combinations of the K-dimensional vector [C1, C2…. CK] form the codebook. Only the index of the codeword in the codebook is sent instead of the quantized values. This conserves space and achieves more compression. |
CODEBOOK GENERATION ALGORITHM |
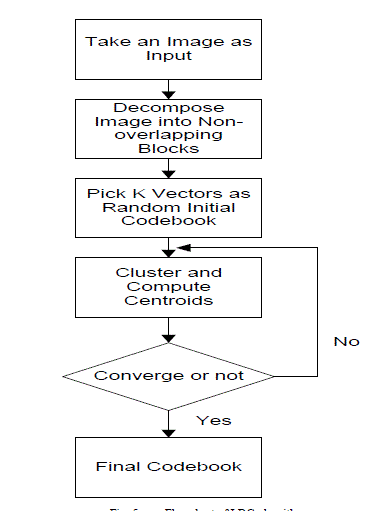
| In 1980, Linde et al. proposed a Generalized Lloyd Algorithm (GLA) which is also called as Linde-Buzo-Gary (LBG) algorithm [8 and 10]. The LBG Algorithm starts with the initialization of a codebook which has the random vectors from the training set. Code vectors are generated with the clustering of training set vectors. The centroid of each code vector is calculated and then interchange with the code vector. This process runs until the distortion in the codebook between iterations reaches a predetermined number. Let X = (x1, x2….. xk) be a training vector and d(X, C) be the Euclidean distance between any two vectors. The iteration of GLA for a codebook generation is given as follows. |
 |
| A. Algorithmic Steps: |
| Step 1: Divide the input image into non overlapping blocks and convert each block into vectors. |
| Step 2: Randomly generate an initial codebook CB0 |
| Step 3: Initialize I = 0. |
| Step 4: Perform the following process for each training vector. |
| Compute the Euclidean distance between all the training vectors belonging to this cluster and the codewords in CBI.q |
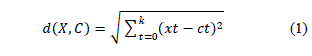 |
| Compute the centroid (code vector) for the clusters obtained in the above step. |
| Step 5: Increment I by one and repeat the step 4 for each code vector. |
| Step 6: Repeat the Step 3 to Step 5 till codebook of desire size is obtained. |
FUTURE ENHANCEMENT |
| The upcoming standard will incorporate many of the research works in vector quantization and will address many important aspects in image compression for the coming years. Future work determines to enhance the wavelet based vector quantization algorithm that performs well for any format of the image. By implementing an effective code book and the wavelet based tree structure the computation complexity can be reduced still more. Interesting issues is like achieving optimal representations of such models, accurate models of images and rapidly computing such optimal representations are the real challenges to the data compression community is facing. The future enhancement may also be focused on developing vector quantization (VQ) algorithms that may ensure less storage space, minimum transfer time and minimum image loading time. The interaction of analysis with the data and image compression, such as the joint source-channel coding, image coding and compression based on models of scalability, human perception, error resilience, robustness and complexity are few of the many outstanding challenges in image compression with vector quantization (VQ) field to be fully resolved and may affect image data compression performance in the years to come. |
CONCLUSION` |
| This paper takes a deep look into the vector quantization, its principal, vector quantization in image compression and the applications of image compression are made in detailed study with examples, and also study of the existing most significant and commonly used methodologies in vector quantization for image compression. The vector quantization methodology extends scalar quantization to higher dimensional space, which is noticeable achievement. By grouping input samples into vectors and using a vector quantizer, a lower bit rate and higher performance can be achieved. |
| As this methodology takes multiple stages discrete wavelet transform of code words and uses them in both search and design processes for the image compression using vector quantization. There is no single algorithm or methodology that satisfies all the requirements that use the vector quantization for image compression as every algorithm has its own merits and demerits. This algorithm can be upgraded to improve image compression efficiency |
References |
|