gb*-Continuity in Topological Spaces

Abstract

In this paper using gb*-closed set in topological spaces due to Dhanya R and A Parvathi [22] we introduced a new class of functions in a topological spaces called  generalized b*-continuous functions (briefly gb*- continuous functions). Further the concept of almost gb*-continuous function and gb*-irresolute function are discussed

Keywords

πgb*-continuous function, πgb*- irresolute function, almost πgb*-continuous function.

INTRODUCTION

Generalized open sets play a very important role in general topology and they are now the research topics of many researchers worldwide. Indeed a significant topic in general topology and real analysis concerns the variously modified forms of continuity, separation axioms etc., by utilizing generalized open sets. Levine [4] introduced the concept of generalized closed sets in topological spaces. Since then many authors have contributed to the study of the various concepts using the notion of generalized b-closed sets. New and interesting applications have been found in the field of Economics, Biology and Robotics etc. Generalized closed sets remains as an active and fascinating field within mathematicians.

RELATED WORK

Levine [4] and Andrijevic [1] introduced the concept of generalized open sets and b-open sets respectively in topological spaces. The class of b-open sets is contained in the class of semipre-open sets and contains the class of semi-open and the class of pre-open sets. Since then several researches were done and the notion of generalized semi-closed, generalized preclosed and generalized semipre-open sets were investigated in [2, 5, 10]. The notion of π-closed sets was introduced by Zaitsev [12]. Later Dontchev and Noiri [9] introduced the notion of πg-closed sets. Park [11] defined πgp-closed sets. Then Aslim, Caksu and Noiri [3] introduced the notion of πgs-closed sets. D. Sreeja and S. Janaki [7] studied the idea of πgbclosed sets and introduced the concept of πgb-continuity. Later the properties and characteristics of πgb-closed sets and πgb-continuity were introduced by Sinem Caglar and Gulhan Ashim [6]. Dhanya. R and A. Parvathi[22] introduced the concept of πgb*-closed sets in topological spaces.

PRELIMINARIES

Throughout this paper (X, τ) represent non-empty topological spaces on which no separation axioms are assumed unless otherwise mentioned. For a subset A of a space (X, τ), cl(A) and int(A) denote the closure of A and the interior of A respectively. (X, τ) will be replaced by X if there is no chance of confusion.

Definition 2.1 Let (X, τ) be a topological space. A subset A of (X, τ) is called

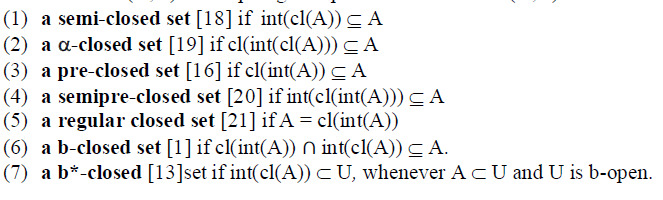The complements of the above mentioned sets are called semi open, α-open, pre-open, semipre-open, regular open, b-open and b*-open sets respectively. The intersection of all semi closed (resp. α-closed, pre-closed, semipre-closed, regular closed and b- closed) subsets of (X, τ) containing A is called the semi closure (resp. α-closure, pre-closure, semipre-closure, regular closure and b-closure) of A and is denoted by scl(A) (resp. αcl(A), pcl(A), spcl(A), rcl(A) and bcl(A)). A subset A of (X,τ) is called clopen if it is both open and closed in (X, τ).

CONCLUSION

The study of πgb*-continuous function is derived from the definition of πgb*-closed set. This study can be extended to fuzzy topological spaces and bitopological spaces.

References

1. [1] D. Andrijevic., “On b-open sets”, Mat. Vesnik, 48, (1996), 59-64.
2. [2] S.P. Arya and T.M. Nour, “Characterizations of s-normal spaces”, Indian J. Pure Appl. Math, 8, 21, (1990), 717-719.
3. [3] G. Aslim, A. Caksu Guler and T.Noiri, “On πgs-closed sets in topological spaces”, Acta Math. Hungar., 112, 4, (2006), 275-283.
4. [4] N. Levine., “Generalized closed sets in topology”, Rend. Circ. Mat. Palermo, 2, 19 (1970), 89-96.
5. [5] H. Maki, J. Umehara and T. Noiri., “Every topological space is pre-T1/2”,Mem.Fac.Sci. Kochi Univ. Ser. A Math.,17, (1996), 33-42.
6. [6] Sinem Caglar Akgun and Gulhan Aslim., “On πgb- Closed Sets and Related Topics” International Journal of Mathematical Archive, 3, 5, (2012), 1873-1884.
7. [7] Sreeja D.and Janaki C., “On πgb-closed sets in topological spaces”, International Journal of Mathematical Archieve, 2, 8, (2011), 1314-1320.
8. [8] M. S.Sarsak and N. Rajesh, “π-Generalized Semi-Preclosed Sets”,International Mathematical Forum, 5 (2010), 573- 578.
9. [9] J.Dontchev and T.Noiri, “Quasi Normal Spaces and πg-closed sets”, Acta Math. Hungar., 89, 3, (2000), 211-219.
10. [10] J.Dontchev.,“On generalizing semi-preopen sets”, Mem. Fac. Sci.Kochi Univ. Ser. A Math., 16, (1995), 35-48.
11. [11] J. H Park, “On πgp-closed sets in Topological Spaces”, Indian J.Pure Appl. Math.,(2004)
12. [12] Zaitsev V., “On Certain Class of Topological Spaces and their bicompactification”, Dokl.Akad.Nauk SSSR 178(1968),pp.778-779.
13. [13] S.Muthuvel and Parimelazhagan., “b*-closed sets in topological spaces”, Int.Journal of Math. Analysis, Vol. 6, 2012, no. 47, 2317-2323.
14. [14] Ahmad-Al-Omari and Mohd.Salmi Md Noorani , “On generalized b-closed sets”, Bulletin of Mathematical Sciences Society, 32, (2009), 19-30.
15. [15] C.Janaki, “Studies on πg∝-closed sets in Topology”, Ph.D Thesis, Bharathiar University, Coimbatore.(2009).
16. [16] Mashhour, A.S., Abd EI-Monsef, M.E. and EI-Deeb, S.N. “On pre-continuous and weak precontinuous mapping”, Proc. Math. Phys. Soc. Egypt., 53, (1982),47 – 53.
17. [17]Maki, H., Devi, R. and Balachandran, K. “Associated topologies of generalized -closed sets and -
generalized closed sets”, Mem. Fac. Sci. Kochi. Univ. Ser.A. Math., 5, (1994),51 – 63.
18. [18] Levine, N. “Semi open sets and semi continuity in topological spaces”, Amer. Math. Monthly, 70,(1963). 36 – 41
19. [19] Njastad, o. On some classes of nearly open sets” , pacific j.Math.,15, (1965),961-970.
20. [20] Andrijevic, D. “Semipre-open sets”,Mat.Vesnnik,38, (1986),24-32.
21. [21] Stone. M Application of the theory of Boolean rings to general topology,Trans.Amer.Math.soc.,41, (1937), 374-481.
22. [22] Dhanya R and A.Parvathi. “On πgb*-closed sets in topological spaces”, IJIRSET, Vol. 3, (2014), Issue 5, 2319-8753.