A Comparative study for ranking the efficiency of washing machines based on fuzzy Set Theory

Abstract

This paper deals with a comparison of the efficiency of different washing machines according to the different types of cloth in a fixed washing time period. The comparison is to be proposed by ranking the different washing machine efficiency using fuzzy set theory where the process evaluation depends on fuzzy membership function and fuzzy logic.

Keywords

Fuzzy set, Fuzzy logic, Membership function, Washing Machine.

INTRODUCTION

Recently washing the cloth with the help of washing machine is increased rapidly in the Indian household. At the present time there are a large number of companies making the washing machine, such as Samsung, LG etc. And the main goal of each company is that to make the product more reliable and to improve the efficiency as a result the machine should optimize the washing time according to different cloth. But controls the reliability of each product with some features is not possible every time. Many conditions are involved to understand the mechanism to increase the reliability and to improve the efficiency, simulation test has been performed before launching the product .Therefore the efficiency parameters are to be selected to perform the simulation .But the problem arises at the time of analyze the result. The result is not getting in numerical values form so to check the efficiency of the product have to depend on the condition where each product is how efficient to wash different type of cloth in a particular time period. Therefore the Boolean operator or linguistic rules are only applicable to describe the result. Testing the product lot of complexity are arises at the time of product testing and these applicable rules are fail to optimize the error of individual machine then the error in measuring the efficiency is large, So this type of experiment is not relevant to optimize the machine work and to overcome this type of problem fuzzy control can be introduced to generate fuzzy rule based system. Fuzzy control washing machines can give the better performance, productivity, simplicity and the less cost, therefore the popularity of such machine has been increased today. Manish Agarwal [1] shown in his paper prescribed the conversion rule from the linguistic input to a well defined output using fuzzy control. Where the input is based on two types of condition such as degree of dirt and type of dirt and the output is taken as a control of washing duration. As a consequence of rule it is also possible to measure washing machine efficiency, according to different cloth to control the washing time. But still the precise mathematical formulation of such condition is not prescribed. Therefore, in this paper the mathematical formulation with particular conditions based on fuzzy set theory is to be described.

Zadeh [9] (1965) first introduced fuzzy set theory and it can be useful where the degree of imprecision is high. The uncertainty nature of any problem can be possible to describe using fuzzy set theory. In the present paper, we will discuss the efficiency of N number of washing machine according to their performance to wash the cloth applying defuzzification method. Various defuzzification methods [3,4,5,6,7] for fuzzy numbers are proposed by various authors. Regarding to our problem membership function construction under certain linguistic conditions is to be proposed to obtain the fuzzy numbers and a defuzzification method [4] with numerical examples will be shown in the next section.

II. PROPOSED METHODOLOGY

II.a. EVALUATION OF MEMBERSHIP FUNCTION

Previously controlling the washing time of a washing machine using fuzzy control has been proposed. To analysed the solution two different types of inputs are taken in consideration. These two variables are as follows

1. Degree of dirt

2. Type of dirt

According to these two variables the washing time is to be measured. In this paper these two variables are considered as fuzzy variables as according to the degree and type of dirt the washing time is varied randomly and uncertainty is present. Now it needs to quantify these two variables according to mathematical relation and for this purpose the membership function of degree of dirt and type of dirt has to be constructed. A set of rules is needed to understand the linguistic condition, according to the input variable degree of dirt and type of dirt. The set of rules implies a well defined relation between the input and output. The rules [1, 2] used as follows:

1. If dirtiness of clothes is large and type of dirt is greasy then wash time is very long.

2. If dirtiness of clothes is a medium and the type of dirt is greasy then wash time is long.

3. If dirtiness of clothes is small and type of dirt is greasy then wash time is long.

4. If dirtiness of clothes is large and type of dirt is medium then wash time is medium.

5. If dirtiness of clothes is small and type of dirt is medium then wash time is medium.

6. If dirtiness of clothes is large and type of dirt is not greasy then wash time is medium.

7. If dirtiness of clothes is a medium and the type of dirt is not greasy then wash time is short.

8. If dirtiness of clothes is small and type of dirt is not greasy then wash time is very short.

Crisp solution is not possible from these rules as these are taken in precise form, therefore the construction of fuzzy values is required it is necessary to define the proper membership function according to the linguistic input (degree of dirt and type of dirt) then it is possible to get crisp values using these rules. Here we denote the membership functions as μD(x) and μT(x) respectively .To construct the mathematical form of membership functions regarding to degree of dirt , the minimum degree of dirt and the maximum degree of dirt are to be considered , where notation used as :

Dmin=degree of dirt is minimum

Dmax=Degree of dirt is maximum

D=Degree of dirt

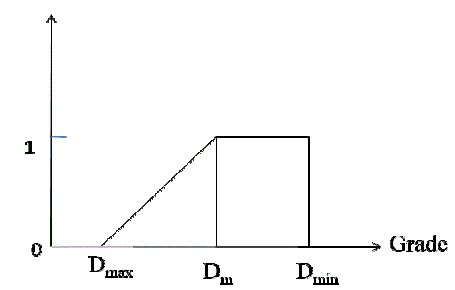
Also to control efficiency of a washing machine, it is obvious that the degrees of dirt of any cloth, which are taken as input, are needed to keep in minimum level. But input are considered as random variables so more chances arise where in the input the degree of dirt can be increased and tends to Dmax. Therefore, to control the washing time a user should consider a random variable in which chances of degree of dirt level is minimum and ,it is consider only to optimize the efficiency of the washing machine and this variable define as Dm. Therefore the characteristic of Dm is depends on Dmin. The variable D is choose as random variable and D is defined as degree of dirt and it can be classified into three subintervals, as follows

Dmax ≤ D ≤ Dm i.e DDmax ,Dm 

Dm ≤ D ≤ Dmin i.e   m min D D ,D

D < Dmax i.e   max D ,D (1)

Applying the particular grading system, it is possible to develop the membership function of degree of dirt using the above rules, denoted as ( ) 0,1 D  x  as follows: also described by the fig 1.

II.b. Ranking method to examine the efficiency of the washing machine

N number of washing machine with same feature are to be considered in order to make ranking on them according to their efficiency which is depend on washing time. According to the previous discussion, degree of dirt is the most useful parameter to control the washing time and to diagnosis the efficiency of the machine. Proportionality relationship between the degree of dirt and type of dirt is observed, which together described the relevant information about the efficiency of the machine. As a type of dirt is high, then the degree of dirt is high and if the type of dirt is low, then the degree of dirt is low. It can be then more convenient to consider the parameter degree of dirt rather than only considering the both parameter degree of dirt and type of dirt. To make the rank it is necessary to consider particular fuzzy number which can generate from the membership function according to degree of dirt, that is previously described by the equation (2). The particular grade system has to consider to distribute the random variables Dmax, Dmin and Dm in between a specific interval and for that purpose, of ranking in between 1 to 10 is to be taken. That means in linguistic term the variables are described as If the degree of dirt is to be maximum,then washing time of individual machine is maximum and then the efficiency of that machine is low therefore the grading point can be low. Everywhere, Dmax [1, 4) to be considered in the calculation. Similarly, if the degree of dirt is minimum then the efficiency of machine is high and highest grading point can be given i.e. min D [8,10].According to predefined definition of Dm ,it is obvious to take them Dm in between (4,8] .Therefore, generate of different type of number is possible after constructing different type of membership function making variation of the random variables Dmax ,Dmin ,Dm ,in between above sub intervals .

III. Solution procedure

T Allah viranloo and R. Saneifard [4] proposed a defuzzification method based on center of gravity in order to rank fuzzy numbers. In this paper this method is used to rank the washing machines according to the efficiency of each machine, where the degree of dirt is considered as a only important parameter to check the efficiency. Assume that there are n fuzzy numbers A1, A2............, An . For ranking fuzzy numbers A1 , A2, ........ An, the existing method is as follows:

Step 1: Calculate the centroid point (xoaj ,yoaj) of each fuzzy number Aj where 1≤j≤n using the following formula

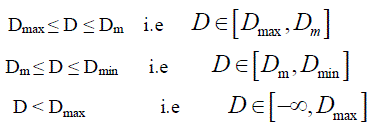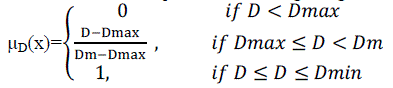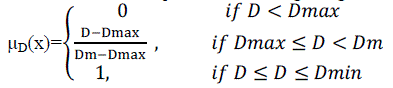V. CONCLUSION

To make ranking according to the efficiency of washing machine a ranking method is described here the main aim is to construct a fuzzy number according to the linguistic conditions. The method is more convenient rather than other ranking method. The obtained fuzzy solution and numerical example of the method can justify the validity of our methodology therefore it can possible to measure the accuracy according to some mathematical formulation which can be generated due to some logical or vague conditions. To generate mathematical formula the construction of membership function is necessary. Here the construction of membership function considers in linear form, further it can be possible to make a distinct form of membership function rather than according to the linear nature of the problem.

References

1. Manish agarwal.Fuzzu logic control of washing machines”
2. Hatem EI-Ayudi, Mohammad T.EI-khozondar,Ibrahim H Banat,Samesh S Abu zer,khalilT Matter,Final year project 1(EELE 5301) fuzzy logic washing machine proposal ,May 2010
3. Shih.Ming Bai,Shyi-Ming Chen.,”evaluating students’learning achievement using fuzzy membership functions and fuzzy rules” 34 (2008) 399-410
4. T.ALLAHVIRANLOO AND R.SANEIFARD,”Defuzzification method for ranking fuzzy numbers based on center of gravity” vol. 9,No. 6 ,(2012) pp 57-67.
5. S.Abbasbandy and B.Asady,Ranking of fuzzy numbers by sign distance,Information sciences,176(2006),2405-2416.
6. Rahim Saneifard,Rasoul Saneifard, a method for defuzzification based on centroid point.Vol.2,No.1, pp. 36-44,2011.
7. R. Saneifard, Another Method for Defuzzification based on Regular Weighted Point.Int. J. Industrial Mathematics(ISSN 2008-5621)Vol.4,No.2, 2012.
8. George J.Klir/Bo Yuan,Fuzzy set and fuzzy logic: theory and application;ISBN:978-81-203-1136-7.
9. L.A .Zadeh, Fuzzy Sets, Information and Control,1965
10. Zimmermann H.J ,Fuzzy set theory, John Wiley & Sons publication