A Generalized Matlab Simulink Model of a Three Phase Induction Motor

Abstract

Induction motors are the most widely used motor drives in industry because of its simple construction and other advantages such as reliable operation, low initial cost, easy operation and simple maintenance, high efficiency and having simple control gear for starting and speed control. This usefulness of this motor has resulted into a lot of research including the transient behaviour of the machine. This paper presents a step by step Simulink implementation of an induction machine using dq0 axis transformations of the stator and rotor variables in the arbitrary reference frame. At first the important formulas are stated and then according to these formulas a generalized model of a three phase induction motor is developed and implemented. The model is used to investigate the effects of variations in the machine size and parameter values on the dynamic performance of induction machine. The proposed system has been developed and simulated by using Matlab/Simulink.

Keywords

Matlab/Simulink, induction motor(IM), dynamic modelling, dq0 axis transformation and Flux linkage.

INTRODUCTION

Dynamic modelling and simulation of induction motor drives is of great importance to both industry and academia due to the prevalence of these types of drives in various industrial settings as well as in the validation of design process of the motor-drive systems, eliminating inadvertent design mistakes and the resulting errors in the prototype constructions and testing [1,2]. The dynamic model of the induction motor is derived by transferring the three-phase quantities into two phase direct and quadrature axes quantities. This paper presents a modular, easy-to-understand Simulink induction motor model [3, 4]. With the modular system [5], each block solves one of the model equations; therefore, unlike in black box models, all of the machine parameters are accessible for control and verification purposes. The power of the proposed tool lies in the ability to study the dynamic behaviour of the induction machine in the absence of complicated mathematics. The program was designed to illustrate clearly the effects of the Park’s transformation [6,7,8,9]. This concept is normally very difficult to learn, but by representing the model of the induction motor in a generic reference frame rotating with an angular speed ω, and simulating some transients, with different operating conditions, one can learn quite well from this concept.

RELATED WORK

In the past, researchers have developed their own software packages for dynamics modeling of induction motor. It is unnecessary to develop user-written software for dynamic model of induction motor when we have proprietary software package such as Matlab/Simulink, licensed by MathWorks which makes simulation design more efficient and allows other interested parties to understand the operation of the system more easily than a programming-language implementation.

Dynamic simulations play an important role in the pre-testing of motor drive systems [9]. Pre-testing is conducted by engineers in industry as well as by researchers in academia. Pre-testing using dynamic simulations can help researchers to determine the experimental setup that will be used for a given set of experimental tests. The transient behaviour of an electric machine is of particular importance when the drive system is to be controlled. Many different methods and control algorithms are available in the literature for controlling the three-phase induction motor [10]. A dynamic model

The induction motor dynamic model and the basic equations that are used in this simulink model are basically taken from the R. Krishan, “Electric motor drives: Modelling, analysis and control [13] and Bimal K.Bose, “Modern Power Electronics and AC Drives,” [14]. Many of the researchers namely M. L. De Aguiar, M. M. Cad, A. Dumitrescu, D. Fodor, T. Jokinen, M. Rosu, S. Bucurencio, S. Wade, M. W. Dunnigan, B. W. Williams developed the induction machine motor models are available in the literature [3,4,15], but they appear to be black boxes with no internal details. Some of them [3,4,15] recommend using S- functions, which are software source codes for Simulink blocks. This technique does not fully utilize the power and ease of Simulink because S-function programming knowledge is required to access the model variables. Reference [16] refers to an implementation of the matlab/simulink approach similar to the one presented in this paper. Similarly, Aleck W. Leedy developed a dynamic model of the induction motor using Simulink / MATLAB that is beneficial for use as a teaching tool in electric machines and power electronics courses as well as a research tool in the laboratory [17].

INDUCTION MOTOR MODEL

The dynamic model of induction motor can be developed by writing differential equations for voltage and torque. For dynamic analysis, poly phase windings are transformed into two phase windings (q-d).In other words; the parameters of an induction machine are transferred to another d-q model which remains stationary [1-4,6,7].

In Fig.1 stator inductance is the sum of the stator leakage inductance and magnetizing inductance (Lls = Ls + Lm), and the rotor inductance is the sum of the rotor leakage inductance and magnetizing inductance (Llr = Lr + Lm). From the equivalent circuit of the induction motor in d-q frame, the model equations are derived. The flux linkages equations associated with this circuit can be found as follows:

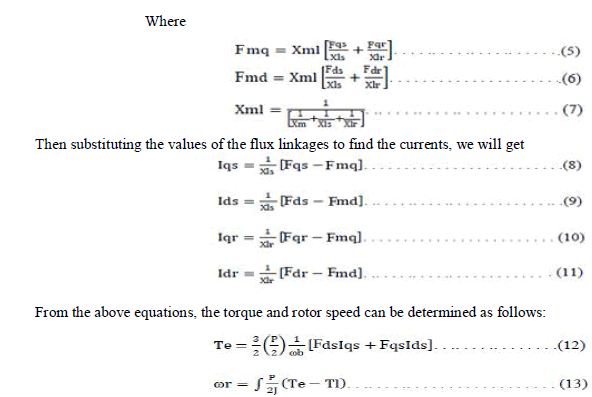Where P: number of poles; J: moment of inertia (Kg/m2). The model constructed according to the equations has been simulated by using MATLAB/SIMULINK. A 3 phase source is applied to conventional model of an induction motor and the equations are given by:

MATLB/SIMULINK IMPLEMENTATION

In this section, the three phase induction machine model is simulated by using the Matlab/Simulink. The Model is implemented using the same set of equations provided above in sections 2. Fig.2 shows the complete Simulink scheme of the described induction machine model.

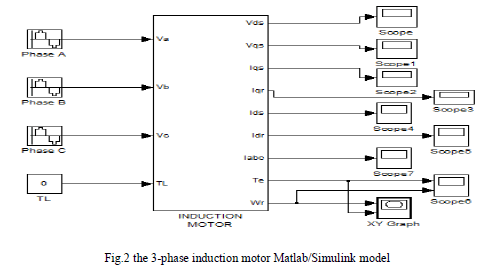The inputs of an induction machine are three phase voltages, their fundamental frequency and the load torque. The outputs of an induction machine are three-phase currents, electrical torque, and rotor speed. In this model the simulation starts with generating a three-phase stator voltages according to the equations (14, 15, 16), and then transforming these balanced voltages to two phase voltages referred to the synchronously rotating frame using Clarke and Park transformation as in equations (17, 18). Fig.3 illustrate the internal structure of the induction machine d-q model by which the flux linkages, currents, torque and the rotor angular speed are calculated.

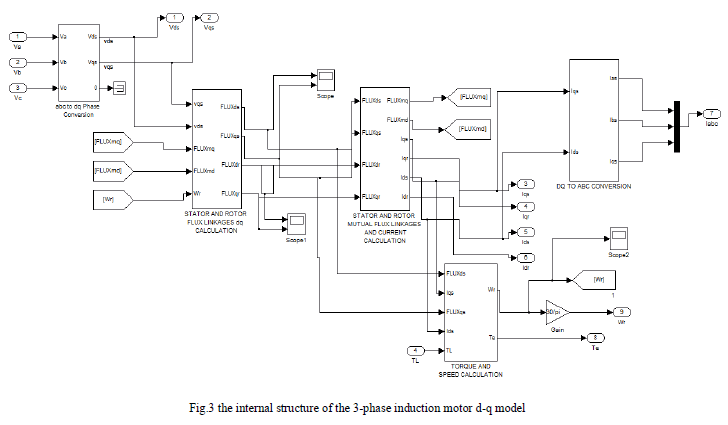Fig.4 shows the Matlab/Simulink model to find the Flux linkage Fqs, Fqr, Fds, Fdr, as stated in equations (1)-(4).

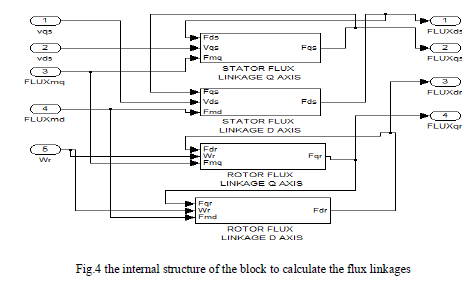Fig.5 shows the internal structure of the blocks of fig.4 in which the equations (1)-(4) are implemented in Matlab/Simulink format.

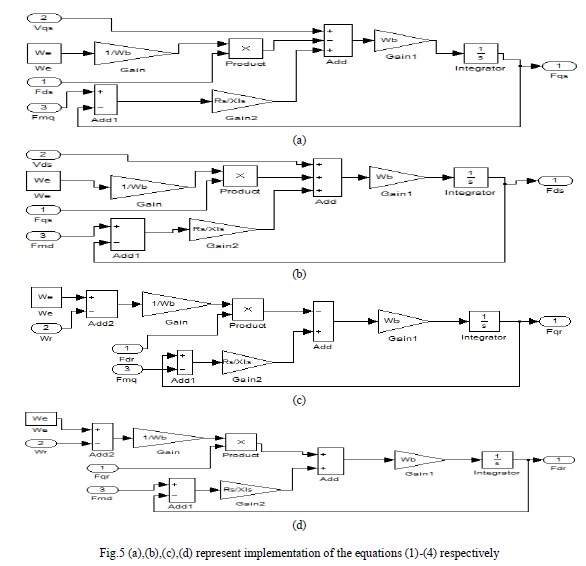Fig.6 shows the Simulink blocks used to calculate the currents Iqs, Ids, Iqr,Idr, according to the equations (8) – (11), also Fmq, Fmd in equations (5), (6). Fig.7 shows the implementation of torque Te and angular speed ωr as expressed in equations (12) and (13) respectively.

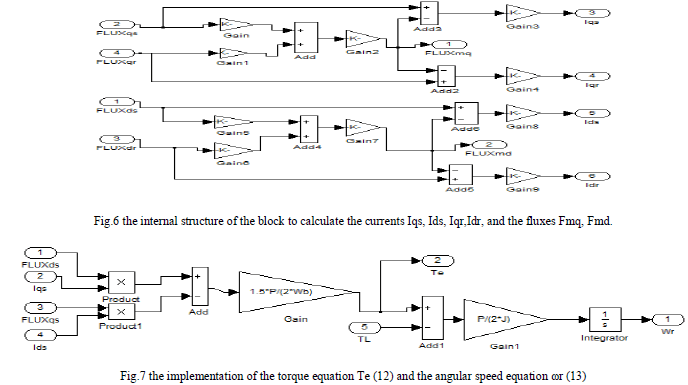MATLAB/SIMULINK RESULTS

The simulation results are given for the induction motor with the following specifications: VL = 1120, P = 4, f = 60, Rs = 0.435, Xls = 0.754, Rr = 0.816, Xlr = 0.754, J = .09, Xlm = 26.13, Speed = 6600rpm (No Load).The machine parameters are defined using graphical user interface (GUI). Fig.8 shows the GUI of the induction machine d-q model.

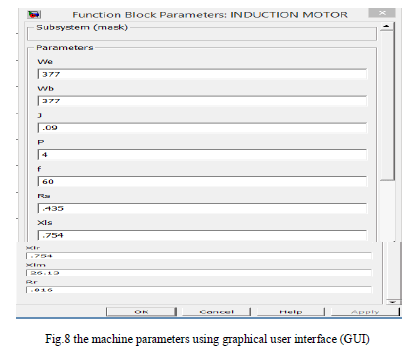The following figures shows the rotor speed, electromagnetic torque, currents and torque- speed curve of the IM at both no load and at a load of 200 N-m.

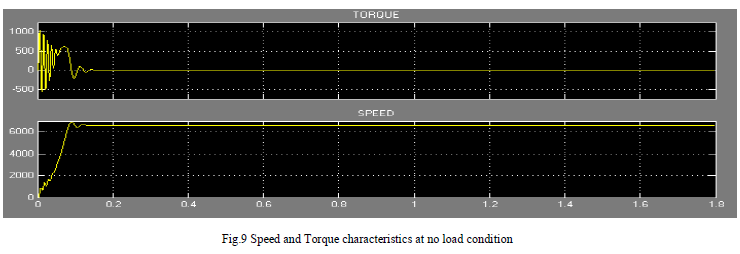Fig.9 shows the rotor speed and torque responses with respect to the time for the IM at no load condition. At time 0.158 seconds speed is 6600 rpm and after that it remains at 6600 rpm. Simultaneously the torque is oscillating between the values of 1032 N-m and -550 Nm up to the speed of 6600 rpm and after that it remains at zero. From this figure we can say that the IM motor quickly attain the speed of 6600 rpm with a stable torque condition.

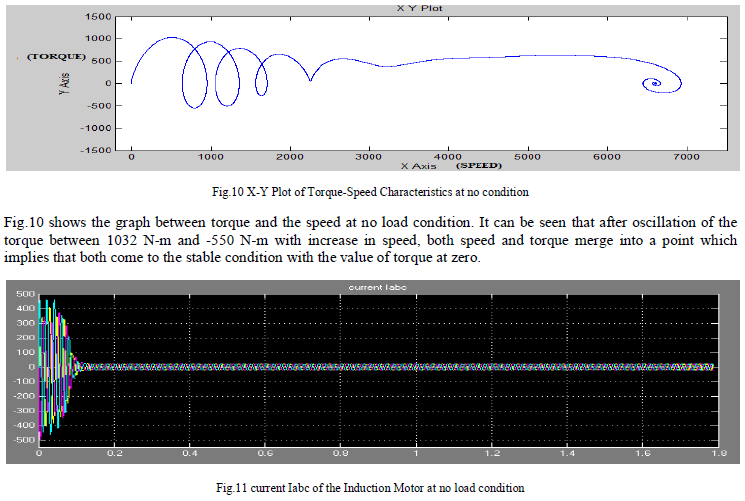Fig.11 shows the rotor current Iabc where before attaining the speed of 6600 rpm, a, b and c axis current components varies between the values of 462 ampere and -503 ampere. After 0.158 seconds, these values of current become stable between the values of 23 ampere and -23 ampere (at the speed of 6600 rpm).

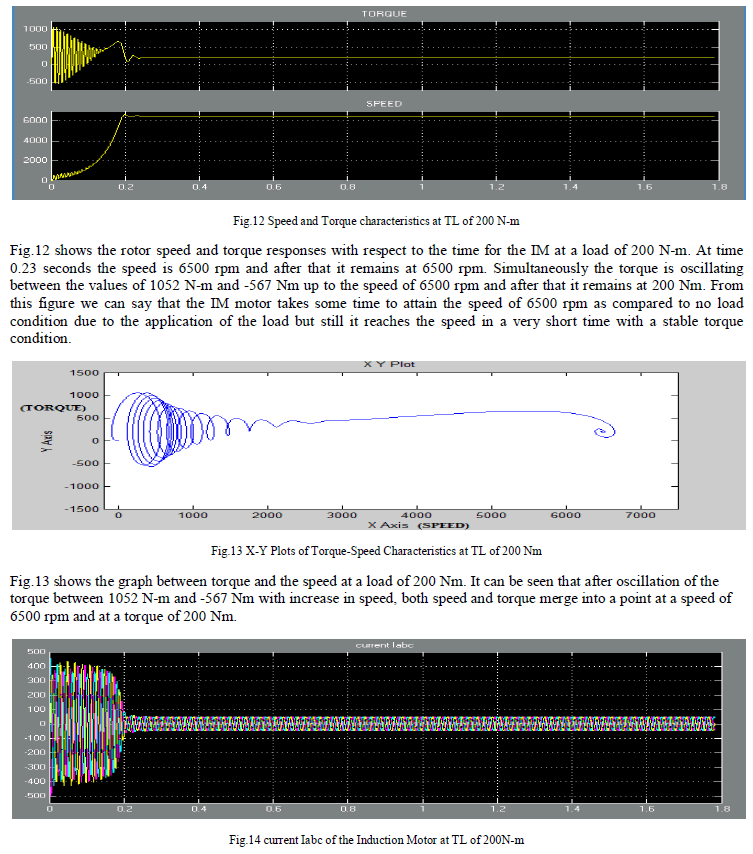Fig.14 shows the rotor current Iabc where before attaining the speed of 6500 rpm, a, b and c axis current components varies between the values of 462 ampere and -503 ampere. After 0.23 seconds, these values of current become stable between the values of 50 ampere and -50 ampere (at the speed of 6500 rpm).

CONCLUSION

In this paper, an implementation of the dynamic modelling of a three-phase induction motor using Matlab/Simulink is presented in a step-by-step manner. The simulated IM model has given a satisfactory response in terms of the torque and speed characteristics. The model was tested at no load condition and load condition. The results concludes that the Matlab/Simulink is a reliable and sophisticated way to analyse and predict the behaviour of induction motor using the theory of reference frames.

ACKNOWLEDGMENT

This research work is made under the guidance of Dr. Neelanjana Baruah (Asscociate professor) of JEC,Assam. I, Lakhya Jyoti Phukon would like to thank my guide and my teachers & my dear friends for helping me in this research work and for their guidance and constant encouragement towards the work.

References

1. [1] P. C. Krause, O. Wasynczuk, S. D. Sudhoff “Analysis of Electric Machinery and Drive Systems”, IEEE Press, A John Wiley & Sons, Inc. Publication Second Edition, 2002.
2. [2] H. C. Stanley, “An Analysis of the Induction Motor”, AIEE Transactions, Vol. 57 (Supplement), pp. 751-755, 1938.
3. [3] M. L. de Aguiar, M. M. Cad, “The concept of complex transfer functions applied to the modeling of induction motors”, Power Engineering Society Winter Meeting, pp. 387–391, 2000.
4. [4] S. Wade, M. W. Dunnigan, B. W. Williams, “Modeling and simulation of induction machine vector control with rotor resistance identification”, IEEE Transactions on Power Electronics, vol. 12, No. 3, pp. 495–506, May 1997.
5. [5] Burak Ozpineci and Leon M. Tolbert, "Simulink implementation of induction machine model - a modular approach," international Conference on Electric Machines & Drives (JEMD), vol.2, pp.728-734,2003.
6. [6] H. C. Stanley, “An Analysis of the Induction Motor”, AIEE Transactions, Vol. 57 (Supplement), pp. 751-755,1938.
7. [7] G. McPherson and R. D. Laramore, “an Introduction to Electrical Machines and Transformers”, 2rd ed., John Wiley and Sons, New York, 1990.
8. [8] Sushma, P. ; Samaga, B.L.R. ; Vittal, K.P. “DQ Modeling of Induction Motor for Virtual Flux Measurement” IPEC, 2010Conference Proceedings, pp. 903 – 908, 2010.
9. [9] D. A. Kocabas, E. Salman, and A.K. Atalay, "Analysis Using D-Q Transformation of a Drive System Including Load and Two Identical Induction Motors," in Proceedings of the IEEE International Electric Machines & Drives Conference (IEMDC), pp. 1575 – 1578, 2011.
10. [10] M.S. Kumar, P.R. Babu, and S. Ramprasath , "Four Quadrant Operation of Direct Torque Control-SVPWM Based Three Phase Induction Motor Drive in MATLAB/Simulink Environment," in Proceedings of the IEEE International Conference on Advanced Communication Control and Computing Technologies (ICACCCT), pp. 397 – 402, 2012.
11. [11] O. Dordevic, N. Bodo, and M. Jones, “Model of anInduction Machine with an Arbitrary Phase Number inMATLAB / Simulink for Educational Use,” inProceedings of the 2010 International UniversitiesPower Engineering Conference (UPEC), pp. 1-6, 2010.
12. [12] O. D. Momoh, “Dynamic Simulation of Cage Rotor Induction Machine – A Simplified and ModularApproach,” in Proceedings of the 44th IEEE Southeastern Symposium on System Theory, pp. 200-203, , 2012.
13. [13] R. Krishnan, Electric Motors Drives Modeling Analysis and control, Publication Prentice Hall of India, 2002.
14. [14] Bimal. K. Bose, Modern Power Electronics & AC Drives, Publication Prentice Hall India, 2003
15. [15] A. Dumitrescu, D. Fodor, T. Jokinen, M. Rosu, S. Bucurencio, “Modeling and simulation of electric drive systems using Matlab/Simulink environments,” International Conference on Electric Machines and Drives (IEMD), pp. 451–453, , 1999.
16. [16] L. Tang, M. F. Rahman, “A new direct torque control strategy for flux and torque ripple reduction for induction motors drive — a Matlab/Simulink model,” IEEE International Electric Machines and Drives Conference, 2001, pp. 884–890.
17. [17] Aleck W. Leedy, “Simulink / MATLAB Dynamic Induction Motor Model for Use as a Teaching and Research Tool,” International Journal of Soft Computing and Engineering (IJSCE), ISSN: 2231-2307, Volume-3, Issue-4, September, 2013
18. [18] H. Le-Huy, “Modeling and simulation of electrical drives using Matlab/Simulink and Power System Blockset,” The 27th Annual Conference of the IEEE Industrial Electronics Society (IECON'01), Denver/Colorado, pp. 1603–1611.
19. [19] MATLAB/SIMULINK® version 2011a, the MathWorks Inc., USA