A New Hyperbolic Shear Deformation Theory for Analysis of Thick Beam

Abstract

A new hyperbolic shear deformation theory for flexure of deep beams, in which number of variables is same as that in the hyperbolic shear deformation theory, is developed. The noteworthy feature of theory is that the transverse shear stresses can be obtained directly from the use of constitutive relations with efficacy, satisfying the shear stress free condition on the top and bottom surfaces of the beam. Hence, the theory obviates the need of shear correction factor. The cantilever isotropic beam subjected to varying load is examined using the present theory. Results obtained are discussed critically with those of other theories.

Keywords

thick beam, new hyperbolic shear deformation, principle of virtual work, equilibrium equations, displacement.

INTRODUCTION

1.1 Introduction It is well-known that elementary theory of bending of beam based on Euler-Bernoulli hypothesis disregards the effects of the shear deformation and stress concentration. The theory is suitable for slender beams and is not suitable for thick or deep beams since it is based on the assumption that the sections normal to neutral axis before bending remain so during bending and after bending, implying that the transverse shear strain is zero. Since theory neglects the transverse shear deformation, it underestimates deflections in case of thick beams where shear deformation effects are significant. 1.2 Literature survey Rayleigh [9] and Timoshenko [10] were the pioneer investigators to include refined effects such as rotatory inertia and shear deformation in the beam theory. Timoshenko showed that the effect of transverse shear is much greater than that of rotatory inertia on the response of transverse vibration of prismatic bars. This theory is now widely referred to as Timoshenko beam theory or first order shear deformation theory (FSDT) in the literature. The first order shear deformation theory (FSDT) of Timoshenko [11] includes refined effects .such as the rotatory inertia and shear deformation in the beam theory. Timoshenko showed that the effect of transverse shear is much greater than that of rotatory inertia on the response of transverse vibration of prismatic bars. In this theory transverse shear strain distribution is assumed to be constant through the beam thickness and thus requires shear correction factor to appropriately represent the strain energy of deformation. Cowper [3] has given refined expression for the shear correction factor for different cross-sections of the beam. The discrepancies in the elementary theory of beam bending and first order shear deformation theory forced the development of higher order or equivalent refined shear deformation theories. Levinson [8], Krishna Murty [7], Baluch, et.al [1], Bhimaraddi and Chandrashekhara [2] presented parabolic shear deformation theories assuming a higher variation of axial displacement in terms of thickness coordinate. These theories satisfy shear stress free boundary conditions on the top and bottom surfaces of the beam and thus obviate the need of shear correction factor. Heyliger and Reddy [6] presented higher order shear deformation theories for the static and free vibration The theories based on trigonometric and hyperbolic functions to represent the shear deformation effects through the thickness is the another class of refined theories. However, with these theories shear stress free boundary conditions are not satisfied at top and bottom surfaces of the beam. This discrepancy is removed by Ghugal and Shimpi [4] and developed a variationally consistent refined trigonometric shear deformation theory for flexure and free vibration of thick isotropic beams. Ghugal and Sharma [5] developed the variationally consistent hyperbolic shear deformation theory for flexure analysis of thick beams and obtained the displacements, stresses and fundamental frequencies of flexure mode and thickness shear modes from free vibration of simply supported beams. In this paper, a variationally consistent hyperbolic shear deformation theory previously developed by Ghugal and Sharma [5] for thick beams is used to obtain the general bending solutions for thick isotropic beams. The theory is applied to uniform isotropic solid beams of rectangular cross-section for static flexure with various boundary and loading conditions. The results are compared with those of elementary, refined beam theory to verify the credibility of the present shear deformation theory. In this paper development of theory and its application to thick cantilever beam is presented.

II. DEVELOPMENT OF THEORY

The beam under consideration as shown in Figure1 occupies in 0  x  y  z Cartesian coordinate system the region:

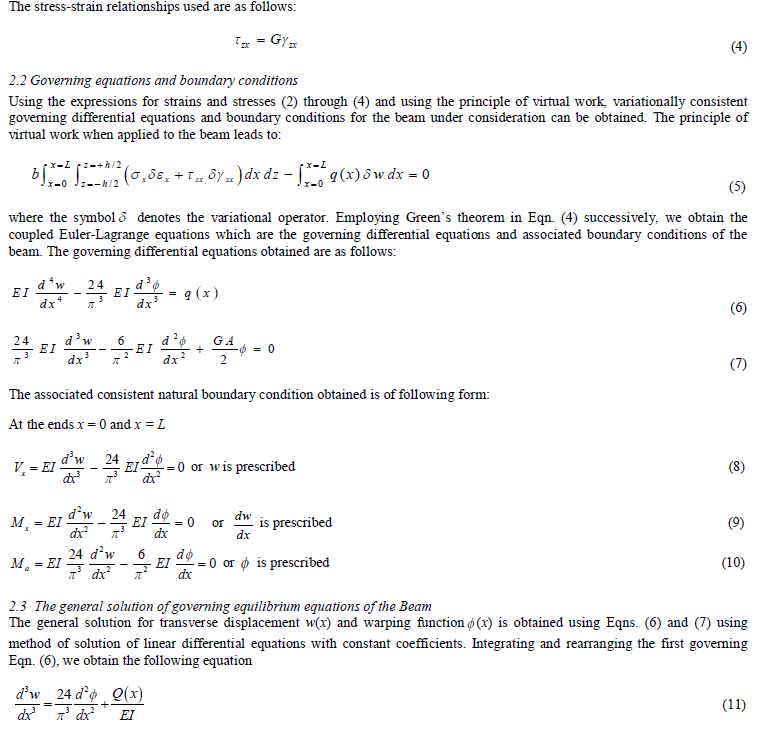V. DISCUSSION OF RESULTS

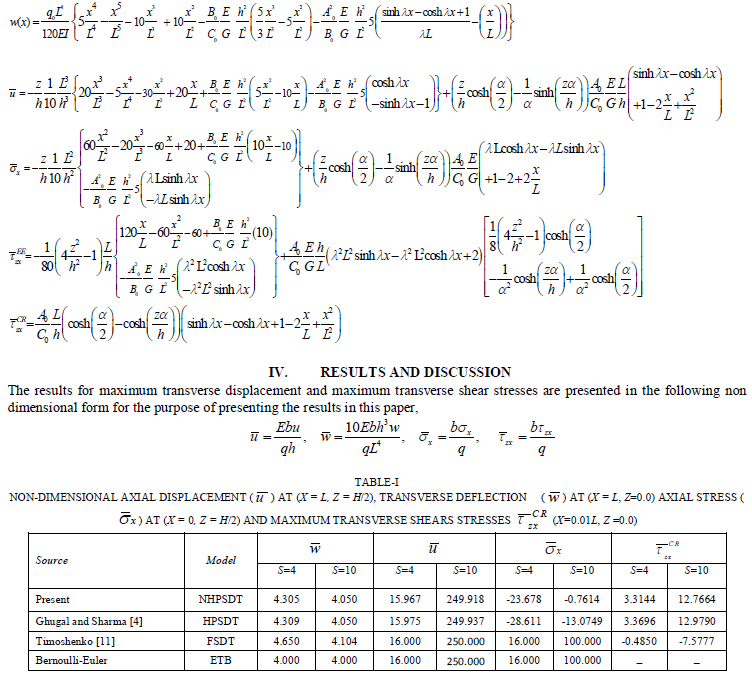
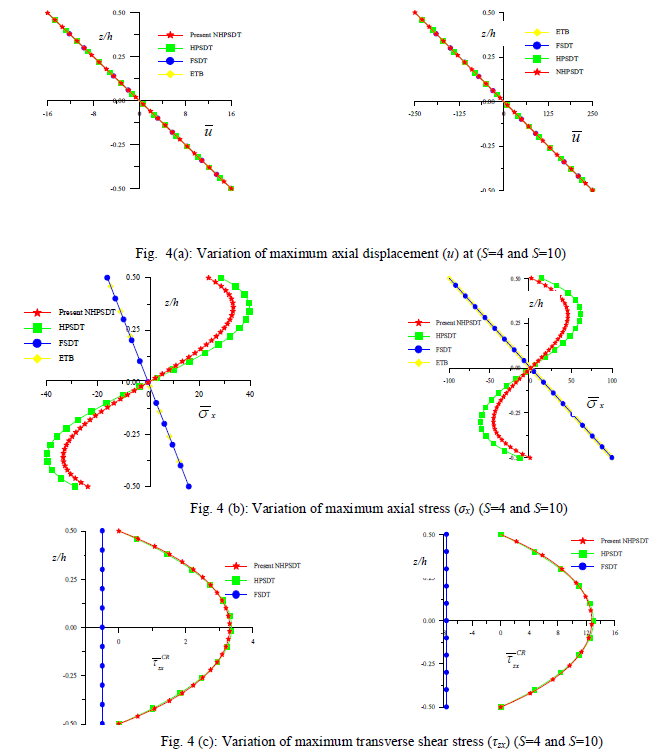
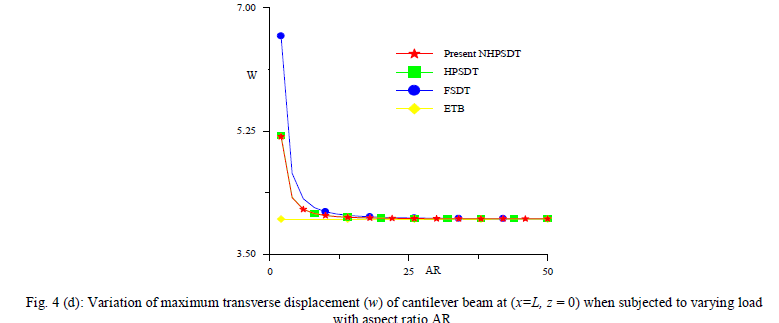
The results obtained by present new hyperbolic shear deformation theory are compared with those of elementary theory of beam bending (ETB), FSDT of Timoshenko, and HPSDT of Ghugal and Sharma. It is to be noted that the exact results from theory of elasticity are not available for the problems analyzed in this paper. The comparison of results of maximum non-dimensional transverse displacement and shear stresses for the aspect ratios of 4 and 10 is presented in Table-I for beam subjected to varying load. Among the results of all the other theories, the values of present theory are in excellent agreement with the values of other refined theories for aspect ratio 4 and 10 except those of classical beam theory (ETB) and FSDT of Timoshenko.

VI. CONCLUSIONS

The variationally consistent theoretical formulation of the theory with general solution technique of governing differential equations is presented. The general solutions for beam with varying load are obtained in case of thick cantilever beam. The displacements and shear stresses obtained by present theory are in excellent agreement with those of other equivalent refined and higher order theories. The present theory yields the realistic variation of transverse displacement through and shear stresses the thickness of beam. Thus the validity of the present theory is established.

ACKNOWLEDGEMENT

am greatly indebted forever to my guide Dr. A.G. Dahake, Asso. Prof. Shreeyash College of Engineering and Technology, Aurangabad for his continuous encouragement, support, ideas, most constructive suggestions, valuable advice and confidence in me. I sincerely thank to Dr. Y.M. Ghugal, Prof. and Head of Applied Mechanics Department, Government College of Engineering, Karad for their encouragement and kind support and stimulating advice.

References

1. Baluch, M. H., Azad, A. K. and Khidir, M. A. Technical theory of beams with normal strain, ASCE J. of Engineering Mechanics, 0110(8), p.1233–37, 1984.
2. Bhimaraddi, A., and Chandrashekhara, K. Observations on higher order beam Theory, ASCE J. of Aerospace Engineering, 6(4), p.408-413, 1993.
3. Cowper, G. R. On the accuracy of Timoshenko beam theory, ASCE J. Engineering Mechanics Division. 94 (EM6), p.1447–53, 1968.
4. Ghugal, Y. M. and Shmipi, R. P. A review of refined shear deformation theories for isotropic and anisotropic laminated beams, J. Reinforced Plastics And Composites, 20(3), p. 255–72, 2001.
5. Ghugal, Y. M. and Sharma, R. A hyperbolic shear deformation theory for flexure and vibration of thick isotropic beams, International J. of Computational Methods, 6(4), p.585–604, 2009.
6. Heyliger, P. R. and Reddy, J. N. A higher order beam finite element for bending and vibration problems, J. Sound and Vibration, 126(2), p.309–326, 1988.
7. Krishna Murthy, A. V. Towards a consistent beam theory, AIAA Journal, 22(6), p.811–16, 1984.
8. Levinson, M. A. new rectangular beam theory, J. Sound and Vibration, 74(1), p.81–87, 1981.
9. Lord Rayleigh J. W. S. The Theory of Sound, Macmillan Publishers, London, 1877.
10. Timoshenko, S. P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars, Philosophical Magazine, 41 (6), p. 742–46, 1921.
11. Timoshenko, S. P. and Goodier, J. N. Theory of Elasticity, McGraw-Hill, 3rd Edition, Singapore. 1970.