A Novel Algorithm for Isomorphic Graph

Abstract

The graph isomorphism difficulty is very famous; isomorphism problem is still one of the unsolved problems of graph theory. Here in this paper we are dealing with some applications of this problem and major idea behind this is advancement of some accessible graph isomorphism algorithms. In this paper we are also focusing on producing the solution for problems that seems like isomorphic problems but they are not exactly isomorphic

Keywords

Isomorphic property, Graph, Sub graph

INTRODUCTION

When humans analyze or synthesize an engineering system by using the mathematical representation governing its behavior, he or she creates a mathematical model of the engineering system, and then writes the equations using knowledge about them and their relation with the physical reality. In usual engineering practice, one uses a model that is known to be suitable for the system at hand and the aim of the computation. Reformulation of the problem into another Formally understood mathematical system [1] [2] [3] to the extent that it is done for engineering analysis, usually uses continuum mathematics. This paper shows that representations of graph theory for engineering problems can be used as a base upon which to extend formal theories of reformulation. Research in engineering analysis usually starts with an understanding of the physical system, then the adoption of a suitable mathematical model for the system. In this work reported different approaches are adopted. Rather than starting with the physical system itself or the mathematical representations historically used for the behavior of engineering systems, many other mathematical approaches were investigated to find those which can be useful representations of engineering systems. Representations were sought for which knowledge of the mathematical properties of those representations and the relations between them can be used to provide augmented understanding of the physical engineering system. For instance, if two engineering systems can be represented by dual, then the physical systems are dual, and this in turn leads to new insights regarding analogies between the systems. The Embedded Engineering Knowledge project [4][5][6][7][8][9] was devoted to searching for representations isomorphic with one or more engineering systems, and finding common properties, if they exist, between them. After investigating many mathematical alternatives, attention was focused on graph theory. This paper illustrates the approach using results only from the graph theory representation, augmented by theorems from graph theory. Graph theory is a useful representation because on the one hand the elements of the graph can be defined so as to have a one-to-one correspondence with the elements of many kinds of engineering systems. On the other hand, the theorems and algorithms of graph theory allow one also to represent behavioral properties of the system, such as deformations and forces, or velocities and movements, as properties of the vertices or edges of the graph [9] [10] [11]. This paper illustrates how engineering problems, for example: truss structures, planetary gear systems and dynamic mass spring dashpot systems are mapped into graphs, and then analyzed by using the theorems and algorithms of graph theory; these theorems and algorithms constitute knowledge that is embedded in the graph theory.

The class of regular graphs looks hard for GI but the regular graphs are reconstructible. We can use this fact in GIalgorithms. Instead of finding the isomorphism between some regular graphs G and H we can try to find out if their decks D (G) and D (H) are isomorphic. We will show on the example of the GI-algorithm from [12] [13] [14] [15] that this method is able to improve some GI-algorithms for regular graphs.

Algorithm: Isomorphic

/*A main idea of the algorithm is a decomposition of the vertex sets V G (resp. VH) into partitions Π = {X1 , . . . , Xk } and (Ψ = {Y1 , . . . , Yl }), where Xi ∩ Xj = ∅ , Yi ∩ Yj = ∅ (for i = j), ∪Xi = VG and ∪Yi = VH . For every vertex x ∈ G (y ∈ H) we denote the number of its neighbors from the set X i (Yi) degG (x, Xi) (degH (y, Yi)).*/

Input: - Graphs G and H;

Let Π = {X1 = VG}, Ψ = {Y1 = VH}, k = 1;

I While the partitions Π, Ψ were refined in the last step do

Begin

A Assign to every vertex x ∈ G (resp. y ∈ H) the sequence (deg G (x, X1) . . . deg G (x, Xk))

(resp. (deg H (y, Y1) . . . deg H (y, YK)))

B Form new partitions Π = {X1 , . . . , Xl }, Ψ = {Y1 , . . . , Ym} /*where ∀x, x ∈G x, x ∈Xi ⇐⇒ (deg G (x, X1 ), . . . , deg G (x, Xk )) = = (deg G (x, X1 ), . . . , deg G (x, Xk )) and the same holds for ∀y, y ∈H*/

C Let Π = Π , Ψ = Ψ (Π = {X1 , . . . , Xl }, Ψ = {Y1 , . . . , Ym });

D if m = l then stop −→ G, H are not isomorphic;

E if k = m = l then Π, Ψ were not changed in this step else let k = m;

F if there are x ∈ Xi , y ∈ Yj such that (deg G (x, X1 ), . . . , deg G (x, Xk )) = (deg H (y, Y1 ), . . . , deg H (y, Yk )) and |Xi | = |Yj | then stop −→ G, H are not isomorphic

End

Order Ψ in such a way as ∀x ∈G, ∀y ∈H and ∀i∈{1, . . . , k} (x ∈ X i )&(y ∈ Yi ) ⇐⇒ (deg G (x, X1 ), . . . , deg G (x, Xk )) = (deg H (y, Y1 ), . . . , deg H (y, Yk ));

G For every bisection f : VG → VH for which f (x) = y ⇐⇒ ∃i (x∈ Xi )&(y∈ Yi )

Do

II if f is an isomorphism then stop → G, H are isomorphic;

Else G, H isn’t isomorphic;

The most important condition to prove isomorphism of a graph is that

1. The number of vertices is same

2. The number of edge is same

3. The degree of graph is same

But the most important condition to prove graph is isomorphism of a graph is that

 The sub graph of original graph is also isomorphic

Example1:- Two graphs is isomorphic as they follow all condition

Example2:- Two graphs is non isomorphic

Example3:-Two graphs are non isomorphic but they have same property

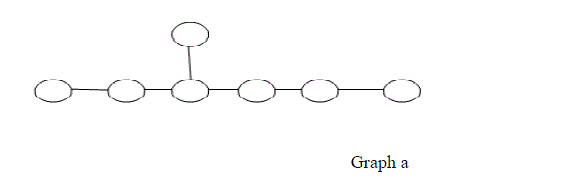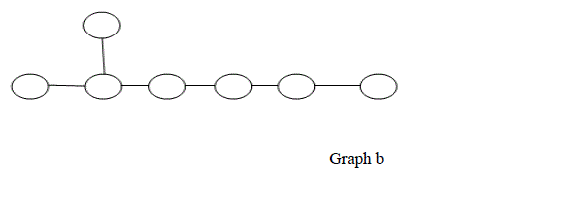II. CONCLUSION

Using the isomorphism algorithm, we have shown that graph is isomorphic only on when the sub graph is also isomorphic that have same number of vertices and edge and also have the same number of degree. In future we will try to design and develop a new technique that is easy to compare that two graph is isomorphic or not.

References

1. Arvind V., Kurur P.P., Graph Isomorphism is in SP P , Electronic Colloqium on Computational Complexity, Report No.37, 2002
2. Babia L., Erdos P., Selkows S., Random Graph Isomorphism, SIAM Journal of˝ Computing, pp.628-635, 1980
3. Boppana R., Hastad J., Zachos S., Does co−N P Have Short Interactive Proofs, Information Processing Letters, pp.27-32, 1987
4. Bosak J., Decompositions of Graphs (in Slovak), VEDA Bratislava, 1986
5. Chen W.Ch., Hierarchy of Graph Isomorphism Testing, Technical Report, Department of Computer Science, California Institute of Technology, 1984
6. Clarke E.M., Enders R., Filkorn T., Jha S., Exploiting Symmetries in Temporal Modal Logic Model Checking, Formal Methods in System Design, 9, 1996
7. Cordella L.P., Foggia P., Sansone C., Vento M., Performance Evaluation of the VF Graph Matching Algorithm, Proc. of the 10th ICIAP, IEEE Computer Society Press, pp.1172-1177, 1999
8. Czimmermann P., Pesko S., The Regular Permutation Scheduling on Graphs, Jour nal of Information, Control and Management Systems, vol.1, 2003
9. Fortin S., The Graph Isomorphism Problem, Technical Report TR 96-20, Department of Computing Science, The University of Alberta, Canada, 1996
10. Garey M.R., Johnson D.S., Computer and Intractability: A Guide to the Theory of N P -completeness, Freeman, San Francisco, 1979
11. Harary F., Graph Theory, Reading(Mass.), Addison-Wesley, 1969
12. Kucera L., Kombinatoricke algoritmy, Praha, SNTL, 1982
13. Ladner R.E., On the Structure of the Polynomial Time Reducibility, Journal of the ACM, pp. 155-171, 1975
14. Lauri J., Vertex-deleted and Edge-deleted Subgraphs, Collected Papers, The University of Malta, 1992
15. Mathon R., A Note on the Graph Isomorphism Counting Problem, Information Processing Letters, pp.131-132, 1979