An Efficient Fast Clustering-Based Feature
Subset Selection Algorithm for High-
Dimensional Data

N.Magendiran; J.Jayaranjani

An Efficient Fast Clustering-Based Feature Subset Selection Algorithm for High- Dimensional Data

N.Magendiran¹, J.Jayaranjani²

Assistant Professor, Dept of CSE, Paavai Engineering College, Namakkal, Tamil Nadu, India
PG Scholar, Dept of CSE, Paavai Engineering College, Namakkal, Tamil Nadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Feature selection is the process of identifying a subset of the most useful features that produces compatible results as the original entire set of features. A feature selection algorithm may be evaluated from both the efficiency and effectiveness points of view. While the efficiency concerns the time required to find a subset of features, the effectiveness is related to the quality of the subset of features. Based on these criteria, a Fast clustering-based feature Selection algorithm (FAST) is proposed and experimentally evaluated. The FAST algorithm works in two steps. In the first step, features are divided into clusters by using graph-theoretic clustering methods. In the second step, the most representative feature that is strongly related to target classes is selected from each cluster to form a subset of features. Features in different clusters are relatively independent; the clustering-based strategy of FAST has a high probability of producing a subset of useful and independent features. The Minimum-Spanning Tree (MST) using Prim’s algorithm can concentrate on one tree at a time. To ensure the efficiency of FAST, adopt the efficient MST using the Kruskal’s Algorithm clustering method.

Keywords

Feature subset selection, filter method, feature clustering, graph-based clustering, Kruskal’s algorithm

INTRODUCTION

Feature selection is an important topic in data mining, especially for high dimensional datasets. Feature selection (also known as subset selection) is an effective way for reducing dimensionality, removing irrelevant data, increasing learning accuracy. Feature selection [14] can be divided into four types: the Embedded, Wrapper, Filter, Hybrid approaches. The Embedded methods incorporate feature selection as part of the training process and are usually specific to given learning algorithms. Decision Trees is the one example for embedded approach. Wrapper model approach uses the method of classification itself to measure the importance of features set, hence the feature selected depends on the classifier model used. Wrapper methods generally result in better performance than filter methods because the feature selection process is optimized for the classification algorithm to be used. However, wrapper methods are too expensive for large dimensional database in terms of computational complexity and time since each feature set considered must be evaluated with the classifier algorithm used [11]. The filter approach actually precedes the actual classification process. The filter approach is independent of the learning algorithm, computationally simple fast and scalable [11]. With respect to the filter feature selection methods, the application of cluster analysis has been demonstrated to show the effectiveness of the features selected from the point of view of classification accuracy [14]. In cluster analysis, graph-theoretic methods have been well studied and used in many applications. The general graphtheoretic clustering is simple: compute a neighborhood graph of instances, then delete any edge in the graph that is much longer/ shorter (according to some criterion) than its neighbors. The result is a forest and each tree in the forest represents a cluster. In our study, we apply graphtheoretic clustering methods to features.

RELATED WORK

Feature subset selection can be viewed as the process of identifying and removing as many irrelevant and redundant features as possible. This is because 1) irrelevant features do not contribute to the predictive accuracy, and 2) redundant feature do not allow to getting a better predictor for that they provide mostly information which is already present in other features [18]. Some of the feature subset selection algorithms eliminate irrelevant features but fail to handle redundant features [2], [3] yet some of others can eliminate the irrelevant while taking care of the redundant features [5], [6]. FAST algorithm falls into second group. The Relief [2], which weights each feature according to its ability to discriminate instances under different targets based on distance-based criteria function. EUBAFES [3] is based on a feature weighting approach which computes binary feature weights and also gives detailed information about feature relevance by continuous weights. EUBAFES is ineffective at removing redundant features. Relief was originally defined for two-class problems and was later extended Relief-F to handle noise and multi-class datasets, but still cannot identify redundant features.

CFS [5] evaluates and hence ranks feature subsets rather than individual features. CFS is achieved by the hypothesis that a good feature subset is one that contains features highly correlated with the target concept, yet uncorrelated with each other. FCBF [6] is a fast filter method which identifies both irrelevant features and redundant features without pair wise correlation analysis. Different from these algorithms, FAST algorithm employs clustering-based method to choose features. In cluster analysis, feature selection is performed in three ways: Feature selection before clustering, Feature selection after clustering, and Feature selection during clustering. In feature selection before clustering, [7] applied unsupervised feature selection methods as a preprocessing step. They raise three different dimensions for evaluating feature selection, namely irrelevant features, efficiency in the performance task and comprehensibility. Under these three dimensions, expect to improve the performance of hierarchical clustering algorithm.

In feature selection during clustering, [8] use genetic algorithm population-based heuristics search techniques using validity index as fitness function to validate optimal attribute subsets. Furthermore, a problem we face in clustering is to decide the optimal number of clusters that fits a data set that is why we first use the same validity index to choose the optimal number of clusters. Then kmean clustering performed on the attribute subset. In feature selection after clustering, [9] Introduce an algorithm for feature selection that clusters attributes using a special metric of Barthelemy-Montjardet distance and then uses a hierarchical clustering for feature selection. Hierarchical algorithms generate clusters that are placed in a cluster tree, which is commonly known as a dendrogram. Use the dendrogram of the resulting cluster hierarchy to choose the most relevant attributes. Unfortunately, the cluster evaluation measure based on Barthelemy-Montjardet distance does not identify a feature subset that allows the classifiers to improve their original performance accuracy. Furthermore, even compared with other feature selection methods the obtained accuracy is lower [14].

Quite different from these hierarchical clustering-based algorithms, our proposed FAST algorithm uses minimum spanning tree-based method to cluster features. Meanwhile, it does not assume that data points are grouped around centers or separated by a regular geometric curve.

FEATURE SUBSET SELECTION

To remove irrelevant features and redundant features, the FAST [14] algorithm has two connected components. Irrelevant feature removal and redundant feature elimination. The irrelevant feature removal is straightforward once the right relevance measure is defined or selected, while the redundant feature elimination is a bit of sophisticated. In our proposed FAST algorithm, it involves 1) the construction of the minimum spanning tree from a weighted complete graph; 2) the partitioning of the MST into a forest with each tree representing a cluster; and 3) the selection of representative features from the clusters.

A. Load Data

The data has to be pre-processed for removing missing values, noise and outliers. Then the given dataset must be converted into the arff format. From the arff format, only the attributes and the values are extracted and stored into the database. By considering the last column of the dataset as the class attribute and select the distinct class labels from that and classify the entire dataset with respect to class labels.

B. Entropy and Conditional Entropy Calculation

Relevant features have strong correlation with target concept so are always necessary for a best subset, while redundant features are not because their values are completely correlated with each other. Thus, notions of feature redundancy and feature relevance are normally in terms of feature correlation and feature-target concept correlation. To find the relevance of each attribute with the class label, Information gain is computed. This is also said to be Mutual Information measure.

Mutual information measures how much the distribution of the feature values and target classes differ from statistical independence. This is a nonlinear estimation of correlation between feature values or feature values and target classes. The Symmetric Uncertainty (SU) is derived from the mutual information by normalizing it to the entropies of feature values or feature values and target classes, and has been used to evaluate the goodness of features for classification. The SU is defined as follows:

Where, H(X) is the entropy of a random variable X. Gain(X|Y) is the amount by which the entropy of Y decreases. It reflects the additional information about Y provided by X and is called the information gain [13] which is given by

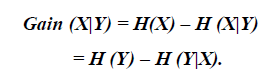Where H(X|Y) is the conditional entropy which quantifies the remaining entropy (i.e., uncertainty) of a random variable X given that the value of another random variable Y is known.

C. T-Relevance and F-Correlation Computation

The relevance between the feature Fi € F and the target concept C is referred to as the T-Relevance of Fi and C, and denoted by SU(Fi,C). If SU(Fi,C) is greater than a predetermined threshold ,then Fi is a strong TRelevance feature. After finding the relevance value, the redundant attributes will be removed with respect to the threshold value. The correlation between any pair of features Fi and Fj (Fi,Fj € ^ F ^ i ≠ j) is called the F-Correlation of Fi and Fj, and denoted by SU(Fi, Fj). The equation symmetric uncertainty which is used for finding the relevance between the attribute and the class is again applied to find the similarity between two attributes with respect to each label.

D. MST Construction

With the F-Correlation value computed above, the MST is constructed. A MST [12] is a sub-graph of a weighted, connected and undirected graph. It is acyclic, connects all the nodes in the graph, and the sum of all of the weight of all of its edges is minimum. That is, there is no other spanning tree, or sub-graph which connects all the nodes and has a smaller sum. If the weights of all the edges are unique, then the MST is unique. The nodes in the tree will represent the samples, and the axis of the ndimensional graph represents the n features. The complete graph G reflects the correlations among all the target-relevant features. Unfortunately, graph G has k vertices and k(k-1)/2 edges. For highdimensional data, it is heavily dense and the edges with different weights are strongly interwoven. Moreover, the decomposition of complete graph is NP-hard. Thus for graph G, build an MST, which connects all vertices such that the sum of the weights of the edges is the minimum, using the well known Kruskal’s algorithm. The weight of edge (Fi`,Fj`) is F-Correlation SU(Fi`,Fj`).

Kruskal's algorithm is a greedy algorithm in graph theory that finds a MST for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a MST for each connected component). If the graph is connected, the forest has a single component and forms a MST. In this tree, the vertices represent the relevance value and the edges represent the F-Correlation value.

E. Partitioning MST and Feature subset selection

After building the MST, in the third step, first remove the edges whose weights are smaller than both of the TRelevance SU(Fi`, C) and SU(Fj`, C), from the MST. After removing all the unnecessary edges, a forest F is obtained. Each tree Tj € F represents a cluster that is denoted as V (Tj), which is the vertex set of Tj as well. As illustrated above, the features in each cluster are redundant, so for each cluster V (Tj) chooses a representative features whose T-Relevance is the greatest. All representative features comprise the final feature subset.

F. Classification

After selecting feature subset, classify selected subset using Probability-based Naïve Bayes Classifier with the help of bayes concept.. Thus the naïve bayes based classifier able to classify in many categories with the various label classification and feature selections from the output of the kruskal’s where it generates the some filtered that MST values, Which can formulates some cluster view with the help of the naïve bayes concepts.

CONCLUSIONS

An Efficient FAST clustering-based feature subset selection algorithm for high dimensional data improves the efficiency of the time required to find a subset of features. The algorithm involves 1) removing irrelevant features, 2) constructing a minimum spanning tree from relative ones, and 3) partitioning the MST and selecting representative features. In the proposed algorithm, a cluster consists of features. Each cluster is treated as a single feature and thus dimensionality is drastically reduced and improved the classification accuracy.

References

H. Almuallim and T.G. Dietterich, “Algorithms for Identifying Relevant Features,” Proc. Ninth Canadian Conf. Artificial Intelligence, pp. 38-45, 1992.
I. Kononenko, “Estimating Attributes: Analysis and Extensions of RELIEF,” Proc. European Conf. Machine Learning, pp. 171-182, 1994.
M. Scherf and W. Brauer, “Feature Selection by Means of a Feature Weighting Approach,” Technical Report FKI-221-97, Institut fur Informatik, Technische Universitat Munchen, 1997.
R. Kohavi and G.H. John, “Wrappers for Feature Subset Selection,” Artificial Intelligence, vol. 97, nos. 1/2, pp. 273-324, 1997.
M.A. Hall, “Correlation-Based Feature Selection for Discrete and Numeric Class Machine Learning,” Proc. 17th Int’l Conf. Machine Learning, pp. 359-366, 2000.
L. Yu and H. Liu, “Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution,” Proc. 20th Int’l Conf. Machine Leaning, vol. 20, no. 2, pp. 856-863, 2003.
Luis Talavera, “Feature Selection as a Preprocessing Step for Hierarchical Clustering,” 2000.
Lydia Boudjeloud and Fran¸cois Poulet, “Attribute Selection for High Dimensional Data Clustering,” 2007.
R. Butterworth, G. Piatetsky-Shapiro, and D.A. Simovici, “On Feature Selection through Clustering,” Proc. IEEE Fifth Int’l Conf. Data Mining, pp. 581-584, 2005.
Hui-Huang Hsu and Cheng-Wei Hsieh,” Feature Selection via Correlation Coefficient Clustering,” JOURNAL OF SOFTWARE, VOL. 5, NO. 12, 2010.
E.R. Dougherty, “Small Sample Issues for Microarray-Based Classification,” Comparative and Functional Genomics, vol. 2, no. 1, pp. 28-34, 2001.
J.W. Jaromczyk and G.T. Toussaint, “Relative Neighborhood Graphs and Their Relatives,” Proc. IEEE, vol. 80, no. 9, pp. 1502- 1517, Sept. 1992.
J.R. Quinlan, C4.5: Programs for Machine Learning. Morgan Kaufman,1993.
Qinbao song, jingjie Ni and Guangtao Wang, “A Fast Clustering- Based Feature Subset Selection Algorithm for High-dimensional Data, IEEE Transaction on knowledge and data Engineering, vol. 25, no. 1,2013.