ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Yasmin Khan1 and Athar Ali Khan2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Weibull distribution is one of the most important and flexible distributions in survival analyses. In this paper, Bayesian regression analysis with censoring mechanism is carried out for a hypothetical survival data problem. Throughout the Bayesian approach is implemented using R and appropriate illustrations are made
Keywords |
| Bayesian Inference, Right censoring, LaplaceApproximation, Survival function. |
I. INTRODUCTION |
| Survival analysis is used when we wish to study the occurrence of some event in a population of subjects and the time until the event is of interest. This time is called survival time. In literature there are many different modeling approaches to survival analysis. In this paper modeling is done by Weibull distribution. There are many life time models but Weibull is used quite effectively to analyzed skewed data sets. Probability density and survival functions of Weibull model is respectively given as |
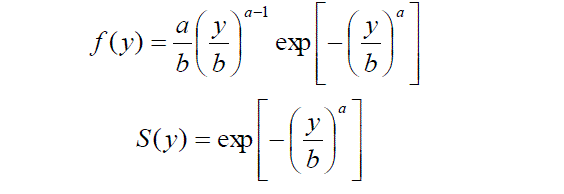 |
| A very important feature which create a special problem in survival analysis, called censoring mechanism. In this paper an attempt has been made to handle the complexity occurs due to censored observation under Bayesian paradigm and we discussed only about right censoring. The likelihood function for right censored data as, |
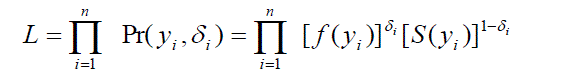 |
| Where i ïÃÂä is an indicator variable which takes value 1 if observation is censored and 0 otherwise. Section III includes the hypothetical survival data of fifteen patients with censoring suffering from a disease and they were treated by two different treatments. Section IV and Section V consist of Bayesian regression analysis of treatment 1 and treatment 2 using LaplacesDemon Hall [1] package which is available in R R Development Core Team[2]. The goal of LaplacesDemon is to provide a complete and self-contained Bayesian environment within R. The main function of this package which is used in the paper is LaplaceApproximation. This function gives the approximated posterior estimates of the parameters in Bayesian framework. In order to deal with censoring mechanism we have developed a function which works well for the analysis of survival data. Comparison of survival curves for two treatments by using Weibull model is reported in section VI. Finally in the last a brief discussion and conclusion is given in section VII. |
II. RELATED WORK |
| A significant amount of work has been done for estimating the linear regression model for censored data Miller[3], Buckley and James[4], Koul, Susarla, and Van Ryzin[5] and Collet[6]. Puja et al. [7] discuss the Bayesian survival analysis of head and neck cancer data and conclude that which therapy has give better performance for patients. In this paper all analyses and computation were undertaken using R software. |
III.DATA SET |
| For illustrative purpose a hypothetical data set given in Table I will be used. The event for this data set is the death of the patients, and so the censored data are those where the outcome is survived or unknown. Bayesian fitting of Weibull model for this data can be done in R by using laplace approximation. Here, fitting is done between survival time as response variable and treatment and age as regressors. |
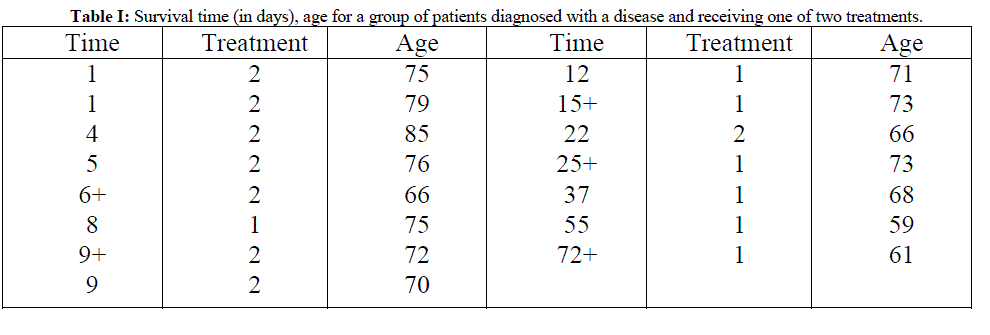 |
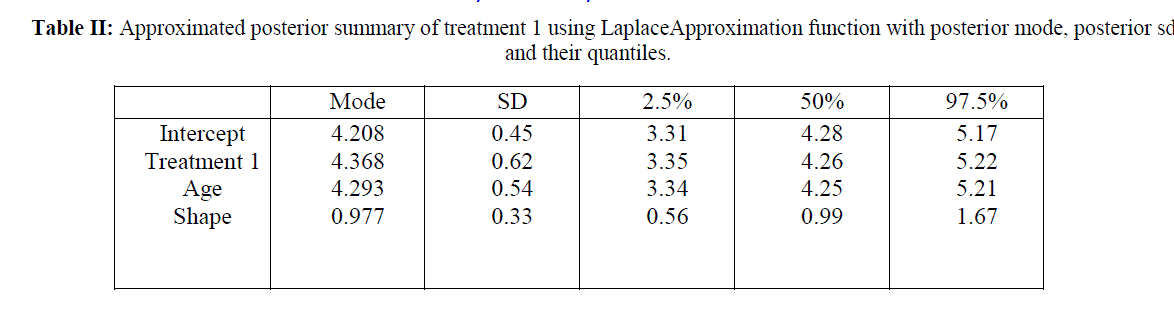
IV. BAYESIAN REGRESSION ANALYSIS FOR TREATMENT 1 OF THE DATA |
| The Weibull distribution is a parametric function widely used in survival analysis. Weibull distribution has two parameters, shape and scale. |
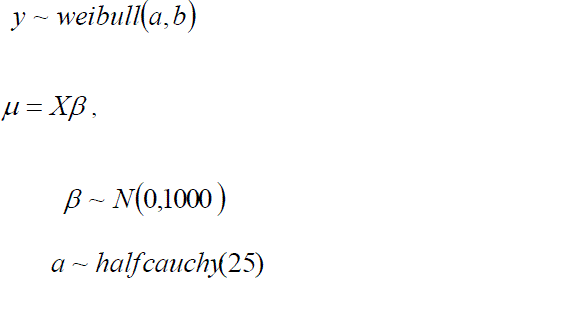 |
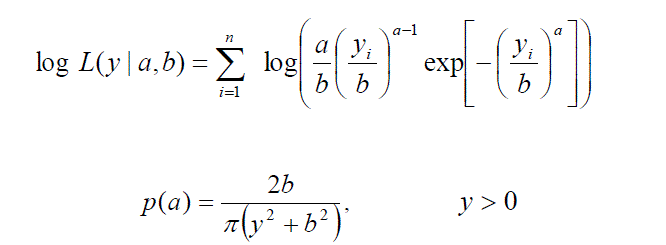 |
 |
 |
V. BAYESIAN REGRESSION ANALYSIS FOR TREATMENT 2 OF THE DATA |
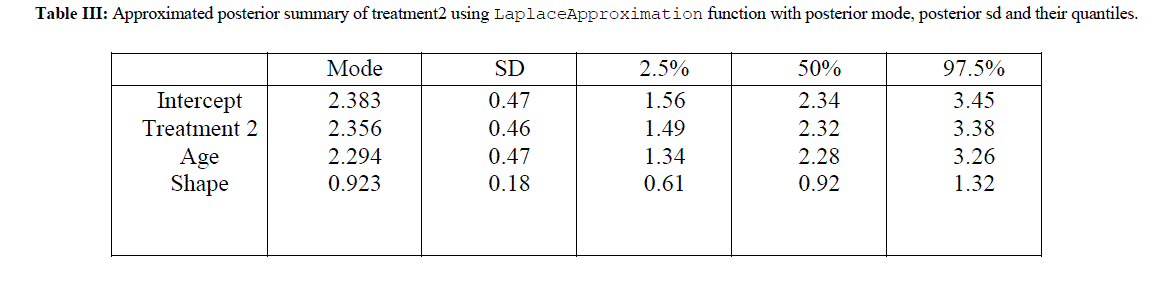
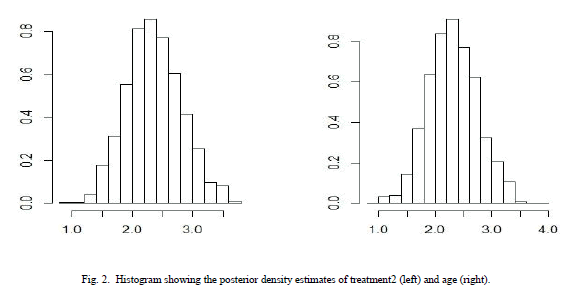
| The R codes for the analysis of treatment 2 is almost same as given in section IV and are not shown here just to save the space. The approximated posterior summary is reported in Table III. Table III gives the posterior mode and posterior sd for treatment 2 also given with respective quantiles. |
 |
 |
VI. COMPARISON OF THE TWO TREATMENTS BASED ON ESTIMATED SURVIVAL FUNCTION |
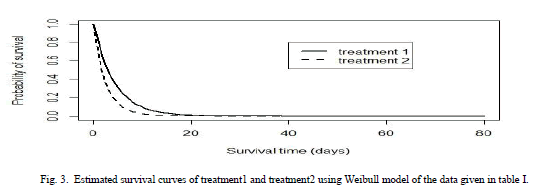
| Survival curves are used to study times required to reach any well-defined endpoint. In this section we will compare the Bayes estimate of survival function based on Weibull model in order to made conclusion that which treatment is better for the patients. It could be seen that the patients receiving treatment1 have higher survival probabilities than those receiving treatment2. |
 |
VII. CONCLUSION |
| Survival analysis and Bayesian methods are the two most active areas in the statistical literature. Survival problems become more complicated because of the presence of censoring. This paper successfully handles and manages censoring mechanism. Laplace approximation has made a great contribution for Bayesian estimation. Numerical and graphical illustrations are made for a hypothetical data. In this data patients suffering from the disease are observed of their survival times when treated with two different treatments. |
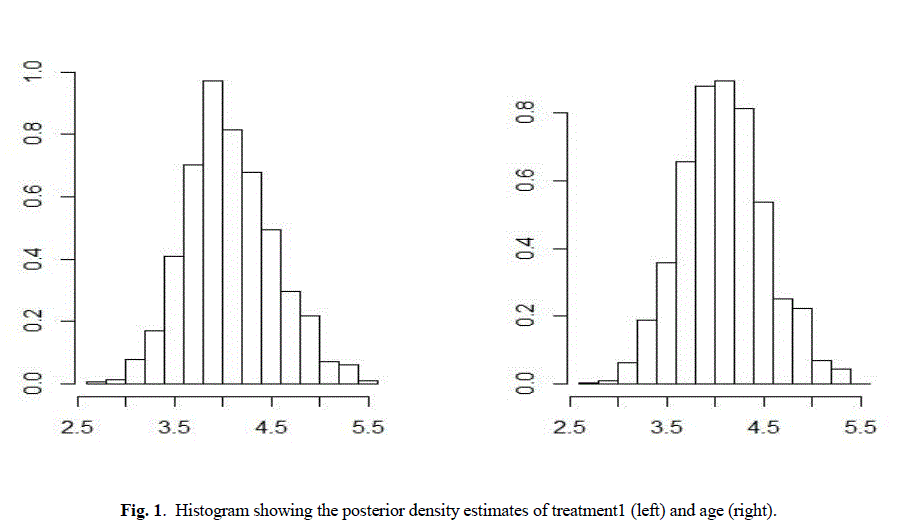
| Table II and table III summarizes the posterior mode and sd and the associated covariance matrix. Assuming normality, these outputs characterizes the marginal posterior distributions. This analysis is done under Weibull model because survival data are generally not symmetric and are positively skewed and Weibull model is also skewed in nature. The posterior density estimates of treatment 1 and age and treatment 2 and age of the data is shown in the form of histogram in Fig 1 and Fig 2 respectively. Comparing survival functions for two treatments in section V has always been an important task for medical data analyst. On the basis of this comparison it could be concluded that treatment 1 offers a better performance for patients than treatment 2 using Weibull model. |
ACKNOWLEDGEMENT |
| The author would like to thank University Grants Commission (UGC), New Delhi for financial assistance. |
References |
|