ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
K.Kavitha1, S.Arivazhagan2, D.Sharmila Banu3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Formation of Composite Kernels without incorporating Spectral Features is investigated. A State of Art Spatial Feature Extraction Algorithm for making Novel Composite Kernels is proposed for classifying a heterogeneous classes present in Hyperspectral Images during the unavailability of the Spectral Features. As the classes in the hyper spectral images have different textures, textural classification is entertained. Gray Level Co-Occurrence, Run Length Feature Extraction is entailed along with the Principal Component and Independent Component Analysis. As Principal & Independent Components have the ability to represent the textural content of pixels, they are treated as features. Composite kernels are formed only by using the calculated Spatial Features without using Spectral Features. The proposed Composite Kernel is learned and tested by SVM with Binary Hierarchical Tree approach. To demonstrate the proposed algorithm, Hyper spectral Image of Indiana Pines Site taken by AVIRIS is selected. Among the original 220 bands, a subset of 150 bands is selected. Co-Occurrence and Run Length features are calculated for the selected fifty bands. The Principle Components are calculated for other fifty bands. Independent Components are calculated for next fifty bands. Results are validated with ground truth and accuracies are calculated
Keywords |
| Multi-class, Co-occurrence Features, Run Length features, PCA, ICA, Combined Features, Composite Kernels, Support Vector Machines |
INTRODUCTION |
| Hyper Spectral image classification is the fastest growing technology in the fields of remote sensing and medicine. Hyper spectral images produce spectra of several hundred wavelengths. A Hyper spectral image has hundreds of bands; where as a multi spectral image has 4 to 7 bands only. |
RELATED WORKS |
| The hyperspectral images provide more information for within class discrimination, i.e., they can discriminate between different types of rocks and different types of vegetation while multi spectral images can discriminate between rock and vegetation [1]. Such hyperspectral images can be used effectively to classify the heterogeneous classes which are present in the image. For classification of multi-class information in an image, it is necessary to derive proper set of features and to choose proper classifier. Classification of hyperspectral images is not the trivial task, as it requires so many factors to be concerned, such as (i) the large number of land-cover class to be handled; (ii) High number of spectral bands but low number of the availability of training samples. This phenomenon is known as Hughes Phenomenon [2] or „curse of dimensionality’. As the consequence, „over fitting’ results. i.e., the classifier performs well on the training samples and poor on the testing samples. This Hughes phenomenon must be alleviated; (iii) Nonlinear spread of the data classes. To overcome these problems and to accommodate the negative issues associated with high dimensional datasets, proper classifier should be selected in such a way that it has to support voluminous data, multi class data and the non-linear dataset. Moreover proper features must be fed to the classifiers to obtain the high accuracy rate.In spatial classification, the spatial arrangement of pixels and their contextual values, textural properties are identified by means of the extracted features. Classification can be done by using the extracted Features. To analyse the textural properties, the repetitiveness of the gray levels and the primitives of the gray levels which can distinguish the different classes must be retrieved. By this way, the basic attribute known as feature can be used to identify the region of interest. An extensive literature is available on the pixel-level processing technique, i.e., techniques that assign each pixel to one of the classes based on its extracted features. Classifying the pixels in the multispectral and hyperspectral images and identifying their relevant class belongings depends on the feature extraction and classifier selection processes. Feature extraction is the akin process while classifying the images. Statistical features such as the mean and standard deviation gives the statistical information about the pixels, while the textural features give the inter-relationship between the grey levels [3]. To find the textural properties of the pixels, Co-occurrence features can be derived by using Gray Level Co-occurrence Matrix (GLCM). Deriving the new features according to the application is an innovative process. The Co-occurrence Matrix is used to extract the land-Cover and land-use features of urban areas in [4]. The Co-occurrence features for individual pixels in the wavelet domain are proved as a promising technique in case of monospectral and multispectral images. The Co-occurrence features can also be used in the transformed domain also. Both statistical and Co-occurrence features are calculated for the decomposed wavelet subbands and are used for target detection in [5]-[6]. The Co-occurrence features are extracted in the wavelet packet decomposition and are used to classify the color texture images [7]. The usage of conventional Run Length features such as Short Run Emphasis (SRE), Long Run Emphasis (LRE), Gray Level Non uniformity (GLN), Run Length Non uniformity (RLN) and Run Percentage are explained in [8] and are used for texture analysis. Run Length features are used to analyze the natural textures in [9]. The Dominant Run Length Feature such as Short-run Low Gray Level Emphasis, Short-run High Gray Level Emphasis, Long-run Low Gray Level Emphasis and Long-run High Gray Level Emphasis to extract the discriminant information for successful classification are introduced in [10]. |
| From the literature, it is evident that the care must be shown towards the feature extraction and classifier selection. Co-occurrence features provide the inter pixel relationship which is useful for classification. The runs of gray levels are useful in identifying the objects or classes. Principal and Independent Components are also the representatives of the classes also provides reduced dimensionality. These features are extracted and are separately used for classification in the previous classification works. But in the proposed algorithm Co-occurrence features, Run Length features, Principal Components and Independent Components are combined together to form the Combined Features and are used for classification. Such Combined Features are expected to yield the better spatially classified image even while the spectral data are not available. Hence in the proposed method it is decided to form the class specific Composite Kernels using Combined Features which are suiTable for both large spatially distributed classes and for spectrally similar classes. The usage of Principal and Independent Components gives the dimensionality reduction which leads to the reduced computational time. The rest of the paper is organized in the following manner. Section-III deals with the Proposed Work followed by the Experiment Design as Section-IV. Section-V is dedicated to the Results and Discussions. Section–VI gives the Conclusion about the work. |
PROPOSED WORK |
Feature Extraction |
| As a feature is the significant representative of an image, it can be used to distinguish one class from other. Feature extraction is the significant process while classifying the images. The extracted features exhibits characteristics of input pixel which the basic requirement of the classifier to make decisions about the class belonging of the pixels. The spatial features are extracted from Gray Level Co-occurrence Matrix (GLCM) and Gray Level Run Length Matrix (GLRM) and by Principal Component Analysis and Independent Component Analysis. After extracting such features they are to be combined to form the Combined Features. The Proposed work flow is shown in figure 1. |
Extraction of Gray Level Co-occurrence Features |
| In Texture analysis procedure, relative positions of pixels in image should be considered to get the inter-pixel relationship. In the Co-occurrence Matrix the distance can be chosen from 1 to 8 and the direction can be any one of 00,450,900,1350,1800,2250,2700,3150. From the Co-occurrence matrix the features like energy, entropy, Contrast, Homogeneity, Variance, Maximum Probability, Inverse Difference Moment, Cluster Tendency are extracted by using the formulas shown in Table 1. While calculating the features, „1’ distance and „00’ direction is considered for this experiment |
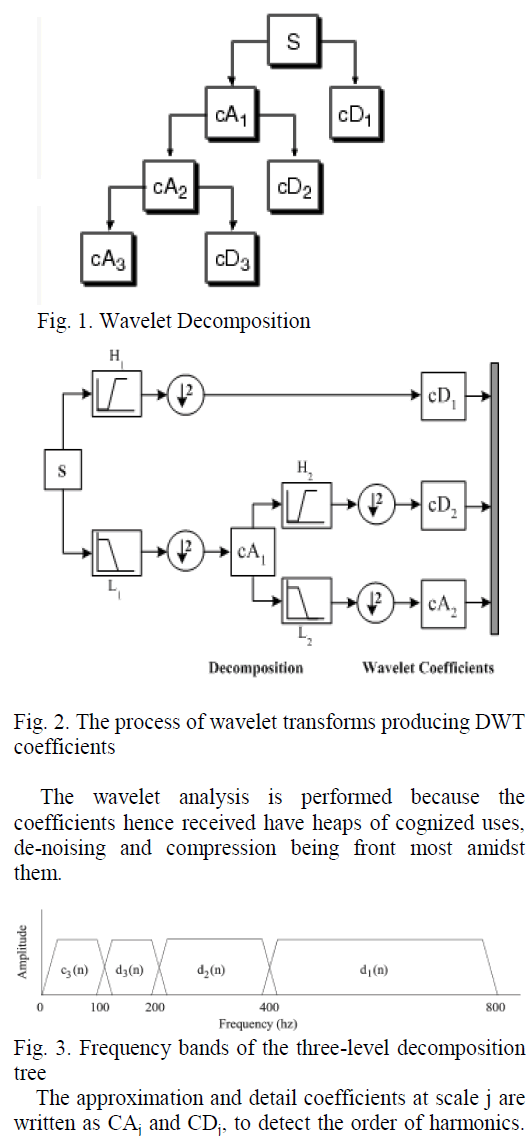 |
| From the GLCM P(i, j), many texture measures can be calculated. The features derived from run-length statistics are shown in table 1. |
Feature Normalization |
| The scales of the eleven different features varied greatly, so they were normalized. The features need to be normalized so that no one feature dominates the others. A feature vector was calculated for each of the images. Form this set of data, a single combined mean feature vector (μ) and a single combined standard deviation vector (σx) are calculated using the combined data from all the classes in the training set. The normalization is done by using the equation (1). |
Extraction of Run Length Features |
| For a given image, an element P(i,j) in the run length matrix „P’ is defined as the number of runs with gray level „i’ and run length „j’. The Run-Length Matrices are calculated in all the four directions (00, 450, 900, 1350). From each Run- Length Matrix, the features are extracted.From the run-length matrix P(i, j), numerical texture measures can be computed and are known as run Length Features. The features derived from run-length statistics are shown in table 2. Where P is the run-length matrix, P (i,j) is an element of the run-length matrix at the position (i,j) and „nr’ is the number of runs in the image. Most features are only functions of run length and not considering the information given by the gray level where as in Co-occurrence features the gray levels are significantly included. So, the Run Length features can able to provide extra spatial information about the classes. |
Extraction of Principal Components |
| PCA is optimal in the mean square sense for data representation. So, the Hyper spectral data are reduced from several hundreds of data channel into few data channels. Hence the dimensionality can also be reduced without losing the required information. |
| The steps involved in Principal Component Extraction are as follows: |
| 1. Get the image |
| 2. Calculate mean and Co-variance matrix |
| 3. Calculate Eigen vectors from the Co-variance matrix |
| 4. Find Eigen values |
| 5. Order the covariance matrix by Eigen value highest and lowest |
| 6. Eigen vectors with highest Eigen value is the Principal Component, which contains significant information |
| 7. Lowest Eigen value components can be discarded |
| The significant components known as Principal Components can be used as the features for classification as they depict more information about the image and are good representatives of image. |
Extraction of Independent Components |
| It is a statistical technique which reveals the hidden factors. As ICA separates the underlying information components of the image data, it can be used as a feature extraction technique. ICA generates the variables which are not only decorrelated, but also statistically independent from each other. PCA makes the data uncorrelated while ICA makes the data as independent as possible. This property is useful in discriminating the different classes in the image. |
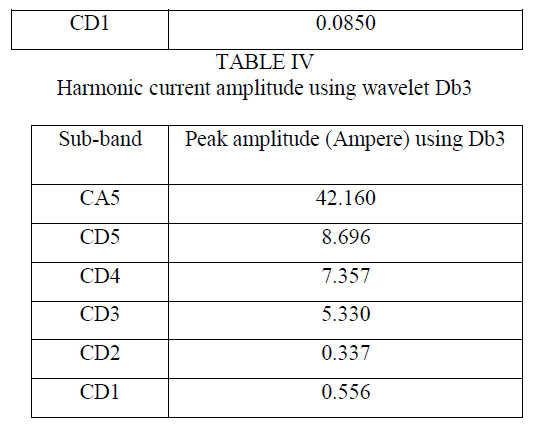 |
ICA features are higher order uncorrelated statistics. While PCA features are second order uncorrelated statistics. Second order statistics may inadequate to represent all the objects in the image. To exploit the information from the multivariate data such as hyper spectral data, higher order statistics are required. ICA features are capable of finding the underlying sources in such applications in which PCA features fail.To identify the independency between classes the linear transformation is required. If the pixels in the corresponding classes depicts zero Mutual Information, then they are assumed as independent. This iterative algorithm finds the direction for the weight vector W maximizing 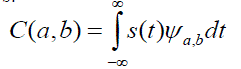 |
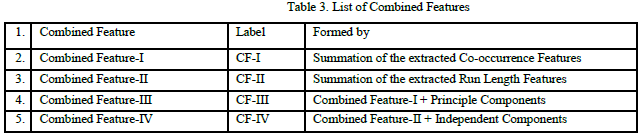
Formation of Combined Features |
| The extracted Co-occurrence, Run Length features, Principle Components and Independent Components are combined as shown in table 3 and are used for classification. |
 |
Support Vector Classifier |
 |
 |
 |
 |
EXPERIMENT DESIGN |
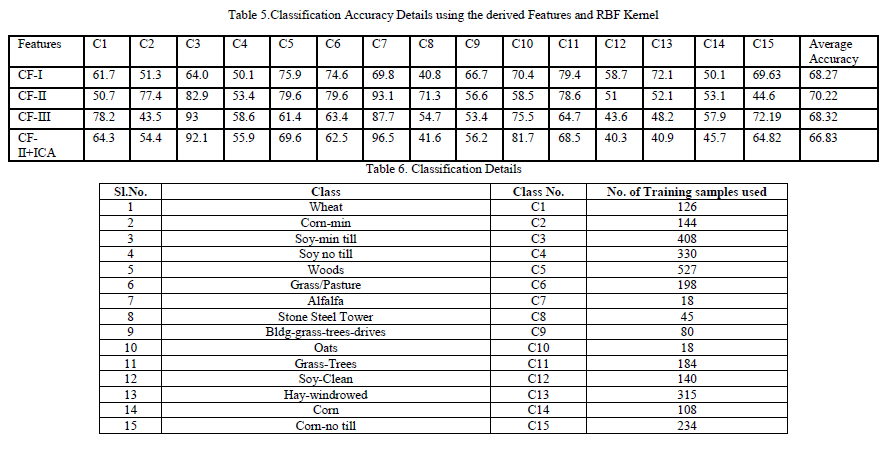
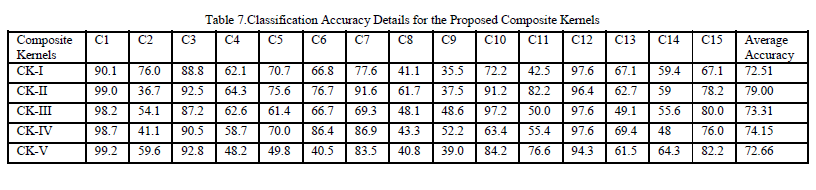
| For evaluating the performance of the proposed method, a sample Hyper Spectral Image which is taken over northwest Indiana’s Indian pine test site is selected. The site is sensed by AVIRIS. The data consists of 220 bands and each band consists of 145 x 145 pixels. The original data set contains 16 different land cover classes Co-occurrence and Run Length Features are calculated for the first fifty bands. Principle Components are calculated for the next fifty bands. Independent Components are calculated for the other fifty bands. First ten Principal Components are used since they contain 99.7% of the information. As it is not the case for Independent Components, all the Independent Components are used. Combined features are made as shown in Table 3. Composite Kernels are formed by using the derived Combined Features. The classification details with training information are shown in Table 6. The performance is validated in the testing phase and the accuracies are quantified and are shown in Tables 5 and 7. |
RESULTS AND DISCUSSIONS |
| Pixels are randomly chosen from each class and their features are used for training. All other pixels are tested against the training samples.The classifier produces the output, whether the pixel under test belongs to the interested trained class or not. Thus the pixels of interested classes are identified among the whole data set. Similarly other classes are also trained. Randomly selected pixels are tested against the training samples. By this way, classes are separated hierarchically. After identifying the pixels of interested class it is labeled and indicated by white gray level. All other pixels are assigned black gray level. Then the pixels are displayed. The output is subtracted from the labeled ground truth and number of misclassified pixels is calculated. The accuracy of each class is calculated and is shown tables 6 and 7. By observing the accuracies, it is evident that the Composite Kernels yield the good accuracies for all the classes than the base kernels.The Co- occurrence and Run Length features are performing equally while they are separately used. The combination of Co-occurrence Features and Principal Components emit comparatively good accuracy than the traditional Co-occurrence feature set. Run Length features along with Independent components exhibit slight increment in the accuracy than the simple Run Length features. Except for few classes the combination of features shows increase in the accuracy.Corn-no till, Corn-Min-till, Soy-no till, Soy-min, Soy-Clean are the most similar classes and their texture variations are also similar. For these classes the conventional features exhibit lower accuracies. |
| But at least one of the proposed Composite Kernels give better result as they provide the cross-information such as Co-occurrence features, Run Length features, Principal Component information and Independent Component information.The spectral responses of the pixels belong to Soy-no till, Soy-min classes are similar. For these cases, the proposed kernels evidence slightly high accuracies than the Spatio-Spectral Composite Kernels available in the literature. Since in Spatio-Spectral Composite Kernels, any one of the spatial features are alone used. But in the proposed algorithm the combined features are used. So it provides the enhanced accuracy. In coarse texture like Alfafa, the gray level runs are longer. But fine texture like buildings takes the short runs. Likewise, the runs of gray levels are varying for each class. So, it is possible for classifying the classes by using Run Length features. For classes like Soybean-min, Alfalfa, the Run Length features have the potential for high accurate classification. |
| But Run Length features fail to distinguish the classes which contain more or less same textural properties. For identifying those classes, which are outliers while using the traditional Run Length features, Principal Components and Independent Components are used. For the class Soy-min, the Run Length features predominates the Co-occurrence features since Soy-min class has the good primitive information for classification which can easily be captured by the Run Length features. The availability of training samples is low for the classes like Alfalfa, Stone Steel Towers, Oats for which, the Principal Components, Independent Components with Co-occurrence features and Run length features respectively advocates good results. But it is not the case for Grass Pasture where both Canonical Analysis methods fail. This combination does not provide helping hand to the classes like Hay and Grass-Pasture mowed. Alfalfa and Grass-Pasture mowed which are assimilated by the neighboring classes. For the class, Woods the conventional methods and formed Composite Kernels are performing equally. But majority of the classes cast their vote to the Composite Kernels alone. Comparison of the measured accuracies are shown in figure 5. |
 |
 |
| Even though the Indiana Pines Data set has low spatial resolution and has mixed pixel effects, the proposed Composite Kernels yield better results than the base kernels. As these Composite Kernels are useful for class specific applications, one can choose this for their domain specific applications too. |
 |
CONCLUSION |
| Even though the proposed Composite Kernels produces slight increment in the accuracy, this may be useful in cases where as the spectral features are not available. One can choose any one of the proposed kernels for class-Specific Applications. It is possible to develop a soft classification algorithm for this type of sensitive classifications. For this case of analysis, knowledge about „which’ class a pixel belongs to is not sufficient. If, the information about, „how much’ the pixel belongs to a particular class is known, it will be more useful for classification. As the Soft Classification extends its application to the sub-pixel levels, it can able to reduce the misclassifications. |
ACKNOWLEDGEMENT |
| The authors are grateful to Prof. David. A. Landgrebe and Prof. Larry Biehl for providing the AVIRIS data set along with the ground truth and for providing the MultiSpec package. |
References |
|