International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

COMMON UNIQUE FIXED POINT THEOREM FOR RANDOM OPERATORS IN HILBERT SPACE

Bijendra Singh1, G.P.S Rathore2, Priyanka Dubey3 ,Naval Singh4
  1. Professor & Dean, School of Studies in Mathematics,Vikram University, Ujjain(M.P), India
  2. Sr.Scientist, K.N.K Horticulture College, Mandsaur(M.P) India
  3. Asst.Professor, Bansal institute of Research &Technology, Bhopal(M.P) India
  4. Asst.Professor, Govt.Science and Commerce College,Benazeer,Bhopal,(M.P) India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The object of this paper is to obtain a common fixed point theorem for four continuous random operators by considering a sequence of measurable functions satisfying certain contractive condition in separable Hilbert space. Mathematics Subject Classification: 54H25,47H10.

Keywords
Separable Hilbert Space, random operators, common random fixed point, rational inequality.

I. INTRODUCTION
The study of the random fixed point theorems in abstract spaces is initiated by Spacek [1] and Hans [2] and are the stochastic generalizations of the classical fixed point theorems in separable Banach spaces.The research along this line gained momentum after the publication of the paper by Bharucha-Reid [3] and since then several random fixed point theorems have been proved in the literature.. Random operator theory is needed for the study of various classes of random equations. Now this theory has become the full fledged research area and various ideas associated with random fixed point theory are used to obtain the solution of non linear random system [4 ,5].The study of the random fixed point theory has attracted much attention in recent years[6,7,8]. These results extend the corresponding result in [9]. In this paper we construct a sequence of measurable functions and consider its convergence to the common unique random fixed point of four continuous random operators defined on a non-empty closed subset of a separable Hilbert space. For the purpose of obtaining the random fixed point of the four continuous random operator, we have used a rational inequality and the parallelogram law.

II. PRELIMINARIES
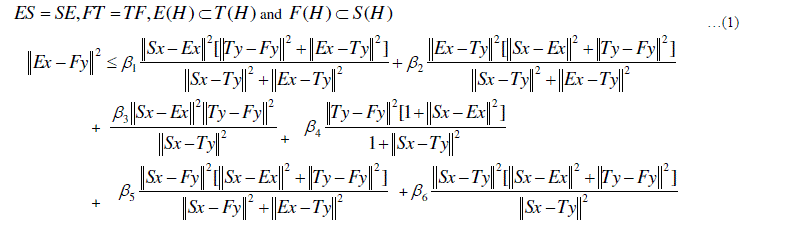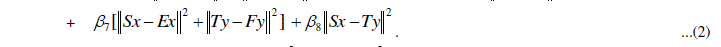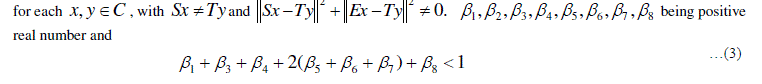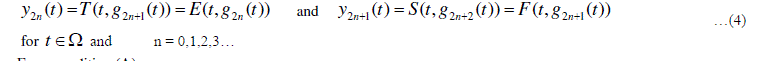image
image
image
image

IV. EXISTENCE OF RANDOM FIXED POINT
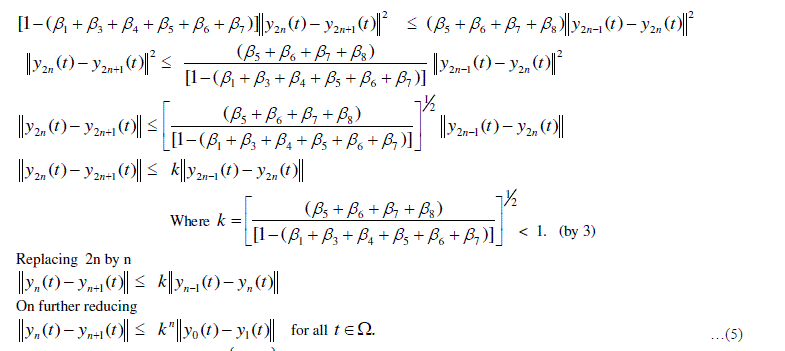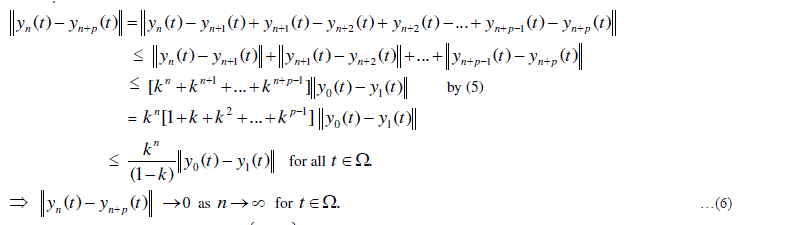image
image
image

References
  1. Spacek.A,Zufallige Gleichungen,Czechoslaviak Math.J.5,462-466(1955).
  2. Hans.P,Random fixed point theorems,Transactions of the first Prague Conference on Information Theory,Statistical Decision Functions,Random Process,pp.105-125,(1957).
  3. Bharucha-Reid. A. T. , Fixed point theorems in probabilistic analysis, Bull. Amer.Math. Soc., 82 ,611-645(1996).
  4. Bharucha-Reid. A. T. ,Random Integral equations Academic Press,New York,1972.
  5. Regan,D.O,Fixed points and random fixed points for weakly inward approximable maps,proceedings of the American Mathematical Society 126 No.10,3045-3053(1998).
  6. Choudhary .Binayak S, A common unique fixed point theorem for two random operators in Hilbert space, IJMMS, 32(3),177 – 182(2002).
  7. Nair .Smita and Shrivastava. Shalu, Fixed point theorem for Hilbert space, Jour. Pure Math. 22, 33 - 37(2005).
  8. Nashine. Hemant kumar, existence of common random fixed point and random best approximation for non-commuting random operators , Bulletin of the Institute of Mathematics Vol. 5 No. 1, pp. 25-40(2010).
  9. Pagey .S. S and Malviya. Neeraj, A Common Unique Random Fixed Point Theorem for rational inequality in Hilbert Space , Int. Journal of Math. Analysis, Vol. 4, no. 3, 133 – 141(2010).
  10. Himmelberg, C.J, Measurable relations, Fund Math, 87, 53 - 72(1975).