COMPARATIVE ANALYSIS OF DIFFERENT FILTERS FOR DENOISING IN MEDICAL IMAGE SEGMENTATION

Manoj kumar V Remya elizabeth philip Arun ASumithra M G

COMPARATIVE ANALYSIS OF DIFFERENT FILTERS FOR DENOISING IN MEDICAL IMAGE SEGMENTATION

Manoj kumar V¹ Remya elizabeth philip² Arun A3Sumithra M G⁴
PG Student, Dept. of ECE, Bannari Amman Institute of Technology, Sathyamangalam, Tamil nadu, India¹
PG Student, Dept. of ECE, Bannari Amman Institute of Technology, Sathyamangalam, Tamil nadu, India²
PG Student, Dept. of ECE,K.Ramakrishnan College of Engineering, Samayapuram, Trichy, India³
Professor, Dept. of ECE, Bannari Amman Institute of Technology, Sathyamangalam, Tamil nadu, India⁴

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Present medical science very much depends on the medical images and medical imaging technology like MRI, CT, US, etc. Doctors are using these medical images for the anatomical structure study and for the treatment planning. But generally medical images are complex and noisy. This paper discuss about the different filters , which eliminate noise and unwanted region without any loss of important information in the image. Rank filter, Gaussian filter, and Sigma filters are general filters using for the de-noising in medical images and these filters are considered for performance comparison in this paper.

Keywords

filter, Image segmentation, de-noising, Rank filter, Gaussian filter, Sigma filter

INTRODUCTION

As the importance of the medical images are increased in the medical field for different application like treatment planning, to locate the tissue, different organs in the human body, and tumours, the importance of the image processing also increased for the accurate analysis of the image for the particular goal [1].

There are different medical image processing like filtering for de-noising, transformation, image enhancement, similarity comparison, registration, segmentation, etc [2]. Segmentation is the one of the important tool in medical image processing, which provides important information from the image.

Segmentation is the process of partitioning an image into semantically interpretable regions. And it partitions an image into a set of non-overlapping regions whose union is the entire image. The purpose of segmentation is to decompose the image into parts that are meaningful with respect to a particular application [1].But generally the medical images are noisy and source of these noises are bit error during the transmission and capturing process like MRI, CT, US, etc. Medical images are also exhibit some nonlinear characteristics like non-uniform intensity and gray level, spreading of region into neighbour region over the boundaries. It indicates the importance of de-noising and equalization of image before the segmentation [3], [4], [6].

De-noising and equalization steps are generally called as pre-processing, because it occurs before the segmentation. Pre-processing step leads to much more accurate result [4], [5]. At the same time the pre-processing should satisfy the condition that should not alter or loss the important information in the medical images. Because medical images are used for the important applications like volume measurement, locate position, etc.

In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal.Different type of filters are available for the de-noising like linear and nonlinear, digital and analog filters, passive and active filter, etc. and should select the filters depend on the application and the characteristics of filter for the particular input [6]. This paper checks the performance and characteristics of the different filters using for the de-noising purpose.

This paper is organized as follows. Section II describes different filters using for de-noising validation parameters. Section III discusses the experimental results. In Section IV conclusion of paper is discussed.

II. IMAGE SEGMENTATION ALGORITHM

Medical images are more used by the doctors, because it has major applications like anatomical structure study, for treatment planning, to identify the tissues and glands and also for its volume measurements. Medical images are the output of the medical imaging technology like MRI, CT, US, etc. But the medical images are generally complex in nature and also noisy. Medical images contain several noises like salt and pepper noise and speckle noise, echo perturbation etc. therefore these noises are should remove before the segmentation process for the correct output. In this work Order filter, Kernel filter, Gaussian filter, Sigma filters are considered for the analysis.

A. Order filter

Rank, median, min, and max filters are the order filters in which the adjacent pixels or the neighbourhood pixels are arranged in an ascending order based on the gray level value and using this order to select the correct value or position. The placement of the value or position within this order set is referred as the rank [6].

n-pixels be sorted into numerical order (V1,V2,V3,……Vn) where V1 ≤ V2 ≤ ……Vn output is then selected, Rank (k) = Vk1≤ k ≤ n (1)

When this is done for all possible window positions,

G = Rk(V) (2)

where V is the input image, G is the processed image and k is the rank position.

Special case of the rank filter is, when the pixel value is odd is the median filter where the median rank position is selected. Other two cases are selecting extreme rank position, one is min filter and other is max filter as shown in equation 3 and 4 [6].

min(V) = R1(V) (3)

max(V) = Rn(V) (4)

B. Gaussian filter

Insignal processing, a Gaussian filter is a filter whose impulse response is a Gaussian function. Gaussian filters are designed to give no overshoot to a step function input while minimizing the rise and fall time. This behavior is closely connected to the fact that the Gaussian filter has the minimum possible group delay. Mathematically, a Gaussian filter modifies the input signal by convolution with a Gaussian function; this transformation is also known as the Weierstrass transform [7].The Gaussian filtering is an important space for the weighted mean filter. It is basedon the shape of the Gaussian function to select the right value of linear smoothingfilter. It usually uses the Gaussian function of discrete two-dimensional by zero-meanto be smoothing filter [7].

The one-dimensional Gaussian filter has an impulse response given by equation 5.

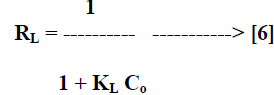where x is the distance from the origin in the horizontal axis, y is the distance from the origin in the vertical axis.

C. Sigma filter

Sigma filter is a non-linear variant of the linear averaging filter aiming to supress noise without blurring the image too much. This filter is motivated by the sigma probability of the Gaussian distribution, and it smooths the image noise by averaging only those neighbourhood pixels which have the intensities within a fixed sigma range of the center pixel. Consequently, image edges are preserved. The filter became polular because it improves noisy images and flattens local differences with minimal loss of sharpness [8].The filter smooths an image by taking an average over the neighbouring pixels, but only includes those pixels that have a value not deviating from the current pixel by more than a given range. The range is defined by the standard deviation of the pixel values within the neighbourhood ("Use Pixels Within ... Sigma"). If the number of pixels in this range is too low (less than "Minimum Pixel Fraction"), averaging over all neighbouring pixels is performed. With the "Outlier Aware" option, averaging over all neighbouring pixels excludes the center pixel. Thus, outliers having a value very different from the surrounding are not included in the average and, thus, completely eliminated [8].

D. Validation

The performance of the filters are validated by some parameters like mean, standard deviation, standard deviation to mean ratio (STM), and mean square error (MSE). Mean is the average value, it may be average intensity or average of pixels in a region. Standard deviation is the most common way to describes the range of variation. STM indicates the ability of a filter to reduce the speckle noise and the MSE, which shows the error value or the difference between the estimated value and the original value [8].

III. EXPERIMENTAL RESULTS

In this section discusses the performance of different filters based on some validation parameters.These filters are generally using for the de-noising before the segmentation of the medical images. In this work brain MRI is considered for the evaluation purpose.

A. Order or Rank filter

Median, min and max are the order filter, these are differed by the rank position. As the name implies the median filter’s rank position is at the middle or in median and the min and max filters are having the extreme rank positions. De-noising using Rank filter is shown in fig 1 and the corresponding parameters are shown in table 1.

Generally the noise is caused by bit errors that occur during data capture or transmission. Since only a small proportion of pixels are encountered as noise and tend to occupy the extreme rank positions. These pixels will not be selected if rank positions near the median are used. Here the minimum rank is 0 and the maximum rank is 10. Rank filter which preserved the shape and edge of the region and it smooth noise. Rank filter changed the mean intensity of the image and no new intensity value is generated. Histogram of the de-noised image using rank filter is shown in fig 2.Fig.2 Histogram of the Rank filters, (a) Histogram of the original image, (b) Histogram of the median filter, (c) Histogram of the max filter, (d) Histogram of the Min filter.

B. Gaussian Filter

When filtering with m x m mask, the Gaussian function is used to find the weights, as shown in equation 6.

Where σ is Gaussian gradient which is user defined. Gaussian filtering is shown in fig 3. The Gaussian gradient is displayed as vector field as shown in fig 3 (d) and the Gaussian gradient σ = 3.5.

Gaussian smoothing is very effective for removing Gaussian noise. The weights give higher significance to pixels near the edge (reduces edge blurring). They are linear low pass filters. Computationally efficient (large filters are implemented using small 1D filters). Rotationally symmetric (perform the same in all directions). The degree of smoothing is controlled by σ (larger σ for more intensive smoothing).

C. Sigma Filter

De-noising using Sigma filter is shown in fig 4. Sigma filter which preserve shape and edge of the different region in the image. The basic idea for the spatial operations is to replace the central voxel by the average of selected neighbour pixels. Due to its close relation to the average filter, the Sigma filter will never provide a stronger smoothing than an ordinary average filter with the same kernel size, but hopefully preserve more edges. All computation is done in the double domain. Here sigma value 1 is used.

Parameters obtained for the sigma and Gaussian filter is shown in table 2.

IV CONCLUSION

De-noising is very important tool in image processing and it is more required in medical images because the medical images are normally complex and having the noises due to bit error in capturing and transmission. It is mandatory to avoid the noise before segmentation for better result. For the de-noising different filters are available like linear and nonlinear filters. Here the described filters are nonlinear filter. Max and Gaussian filters are giving better performance than other rank filter and sigma filter. Max and Gaussian filter provides comparatively good MSE and moderate STM.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

References

Dzung L. Pham, Chenyang Xu, and Jerry L. Princ,”Current Methods In Medical Image Segmentation,” Department of Electrical and Computer Engineering, The Johns Hopkins University,Annu. Rev. Biomed. Eng, 02:315–37, 2000.
Shapiro, L. G. & Stockman, G. C: "Computer Vision", page 137, 150. Prentence Hall, 2001
Krit Somkantha, Nipon Theera- Umpon,,and Sansanee Auephanwiriyakul,”Boundary Detection in Medical Images Using Edge Following Algorithm Based on Intensity Gradient and Texture Gradient Features”IEEE transactions on biomedical engineering, vol. 58, no. 3, march 2011.
Chuan-Yu Chang, Yue-Fong Lei, Chin-Hsiao Tseng, and Shyang-Rong Shih “Thyroid Segmentation and Volume Estimation in Ultrasound Images” IEEE transactions on biomedical engineering, vol. 57, no. 6, JUNE 2010.
Chuan-Yu Chang and Yong-Cheng Hong Pau-Choo Chung, Chin-Hsiao “A Neural Network for Thyroid Segmentation and Volume Estimation in CT Images” IEEE computational intelligence magazine, NOVEMBER 2011.
R M Hodgson, D G Bailey, M J Naylor, A L M Ng and S J McNeil “Properties, implementations and applications of rankfilter” Butterworth& Co (Publishers) Ltd, vol3 no I FEBRUARY 1985.
R.A. Haddad and A.N. Akansu, "A Class of Fast Gaussian Binomial Filters for Speech and Image Processing," IEEE Transactions on Acoustics, Speech and Signal Processing, vol. 39, pp 723-727, March 1991
Leena Vasant Patil, Ketki Kishor Rane, Aadeet i Prashant Salvi ,Department of Information Technology, Usha Mittal Institute of Technology for Women , SNDT Women’s University, Santacruz(w), Mumbai,18 June, 2011.