Design a cryptographic approach for Privacy
Preserving Data Mining

R.Natarajan; Dr.R.Sugumar; M.Mahendran; K.Anbazhagan

Design a cryptographic approach for Privacy Preserving Data Mining

R.Natarajan¹, Dr.R.Sugumar², M.Mahendran³, K.Anbazhagan⁴
Research Scholar, Dept. of CSE, CMJ University, Shillong, Meghalaya, India^1,3,4 Associate Professor, Dept. of CSE, Vel Multitech Dr. RR Dr.SR Engineering College, Chennai, India²

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Privacy preserving data mining is a research area concerned with the privacy driven from personally identifiable information when considered for data mining. This paper addresses the privacy problem by considering the privacy and algorithmic requirements simultaneously. The objective of this paper is to design a cryptographic approach to privacy preserving data mining which would be efficient in providing confidentiality and improve the performance.

Keywords

support, confidence, encryption, asymmetric key

INTRODUCTION

Many government agencies, businesses and non-profit organizations in order to support their short and long term planning activities, they are searching for a way to collect, store, analyze and report data about individuals, households or businesses. Information systems, therefore, contain confidential information such as social security numbers, income, credit ratings, type of disease, customer purchases, etc., that must be properly protected.

Securing against unauthorized accesses has been an long-term goal of the database security research community and the government research statistical agencies. Solutions to such a problem require combining several techniques and mechanisms. In an environment where data have different sensitivity levels, this data may be classified at different levels, and made available only to those subjects with an appropriate clearance. A multilevel secure system would ensure that data at classification levels above the user?s login level would be invisible to that user. Such a system is designed to prevent higher level of data from being directly encoded in lower level data. This can be done by changing the values of lower level data in a particular pattern or by selecting certain visible data for output based upon values of higher level data. It is however, well known that simply by restricting access to sensitive data does not ensure complete sensitive data protection. For example, sensitive or “high” data items may be inferred from non-sensitive, or “low” data through some inference process based on some knowledge of the semantics of the application the user has. Such a problem, known as the “inference problem” has been widely investigated and possible solutions have been identified. The proposed solutions address the problem of how to prevent disclosure of sensitive data through the combination of known inference rules with non-sensitive data. Examples of inference rules are deductive rules, functional dependencies, or material implications.

Recent advances in Data Mining (DM) techniques and related applications have however, increased the security risks that one may incur when is releasing data. The elicitation of knowledge that can be attained by such techniques, has been the focus of the Knowledge Discovery in Databases (KDD) researchers? effort for years and by now, it is a well understood problem. On the other hand, the impact on the information confidentiality originating by these techniques has not been considered until very recently.

The process of uncovering hidden patterns from large databases was first indicated as a threat to database security, by O? Leary, in a paper presented in the 1st International Conference in Knowledge Discovery and Databases. Piatetsky-Shapiro, in GTE Laboratories, was the chair of a mini-symposium on knowledge discovery in databases and privacy, organized around the issues raised in O? Leary?s paper in 1991. The focal point discussed by the panel was the limitation of disclosure of personal information, which is not different in principle from the focal point of statisticians and database researchers since in many fields like medical and socio-economic research, the goal is not to discover patterns about specific individuals but patterns about groups.

The compromise in the confidentiality of sensitive information, that is not limited to patterns specific to individuals, is another form of threat which is analysed in a recent paper by Clifton from Mitre Corporation and Marks from Department of Defence. The authors provide a well designed scenario of how different data mining techniques can be used in a business setting to provide business competitors with an advantage.

The necessity to combine the confidentiality and the legitimate needs of data users is imperative. Every disclosure limitation method has an impact, which is not always a positive one, on true data values and relationships. Ideally, these effects can be quantified so that their anticipated impact on the completeness and validity of the data can guide the selection and use of the disclosure limitation method. In this paper, we propose new strategies and a suite of algorithms for hiding sensitive knowledge from data by minimally perturbing their values. The hiding strategies that we propose are based on reducing the support and confidence of rules that specify how significant they are. In order to achieve this, transactions are modified by removing some items, or inserting new items depending on the hiding strategy. The constraint on the algorithms is that the changes in the database introduced by the hiding process should be limited, in such a way that the information loss incurred by the process is minimal. Selection of the items in a rule to be hidden and the selection of the transactions that will be modified is a crucial factor for achieving the minimal information loss constraint. We also perform a detailed performance evaluation and validation study in order to prove that the proposed algorithms are computationally efficient, and provide certain provisions on the changes that they impose in the original database. According to this, we try to apply minimal changes in the database at every step of the hiding algorithms that we propose.

Today, most of the sensitive data maintained by organizations is not encrypted. This is especially true in database environments, where sensitive data or sensitive patterns are usually included. In the past, parties who sought privacy were hesitant to implement database encryption because of their high cost, complexity, and performance degradation. Recently, with the ever growing risk of data theft and emerging legislative requirements, parties have become more willing to compromise efficiency for privacy.

While traditional ways of database encryption were indeed costly, very complex and created significant performance degradation, fortunately, there are now newer, better ways to handle database encryption. In this chapter, we demonstrate how database encryption can allow parties to share data for the common good without jeopardizing the privacy of each party.

Computation tasks based on data distributed among several parties have privacy implications. The parties could be trusted parties, partially trusted parties or even competitors. To perform such a computation, one of the parties must know the input of all the other parties. When the task is a data mining task, the absence of a trusted third party or a specific mechanism to exchange data in a way that does not reveal sensitive data (for example, by adding noise or perturbing the data so that it does not affect the final desired result), is a challenge for privacy-preserving data mining. When two or more parties want to conduct analysis based on their private data and each party wants to conceal their own data from the others, the problem falls into the area known as Secure Multi-Party Computation (SMC).

II. Preliminaries

A. Horizontal versus vertical distribution

With horizontally partitioned data, each party collects data about the same attributes for objects. For example, hospitals that collect similar data about diseases but for different patients. With vertically partitioned data, each party collects different attributes for the same objects. For example, patients have attributes for a hospital that are different from attributes with insurance companies. If the data is distributed vertically, then unique attributes that appear in a pattern or a transaction can be linked to the owner. In this chapter we assume horizontal distribution of data.

B. Secure multi-party computation

The problem of secure multi-party computation is as follows. A number of N parties, P0, . . . , Pn wish to evaluate a function F(x1, . . . , xn), where xi is a secret value provided by Pi. The goal is to preserve the privacy of the each party?s inputs and guarantee the correctness of the computation. This problem is trivial if we add a trusted third party T to the computation. Simply, T collects all the inputs from the parties, computes the function F, and announces the result. If the function F to be evaluated is a data mining task, we call this privacy-preserving data mining in secure multi-party computation (PPDMSMC).

It is easy to find a trusted party in the medical sector for example, but it is difficult to agree on a trusted party in the industrial sector. The algorithms proposed to solve PPDMSMC problems usually assume no trusted party, but assume a semi-honest model. The semi-honest model is one of two models which are more realistic abstractions of how parties would engage and participate in a collective computation while preserving privacy of their data.

C. Two models

In the study of secure multi-party computation, one of two models is usually assumed: the malicious model and the semi-honest model.

C.1) The malicious model

The malicious party is a party who does not follow the protocol properly. The model consists of one or more malicious parties which may attempt to deviate from the protocol in any manner. The malicious party can deviate from the protocol through one of the following possibilities:

? A party may refuse to participate in the protocol when the protocol is first invoked.

? A party may substitute its local input by entering the protocol with an input other than the one provided to it.

? A party may abort prematurely.

C.2) The semi-honest model

A semi-honest party is one who follows the protocol steps but feels free to deviate in between the steps to gain more knowledge and satisfy an independent agenda of interests. In other words, a semi-honest party follows the protocol step by step and computes what needs to be computed based on the input provided from the other parties, but it can do its own analysis during or after the protocol to compromise privacy/security of other parties. It will not insert false information that will result in failure to compute the data mining result, but will use all the information gained to attempt to infer or discover private values from the data sets of other parties. A definition of the semi-honest model [Gol98] formalises that whatever a semi-honest party learns from participating in the protocol, this information could be essentially obtained from its inputs and its outputs. In particular, the definition uses a probabilistic functionality

computable in polynomial-time. Here, f1(x, y) denotes the first element of f(x, y), and says that what the output string is for the first party as a function of the inputs strings of the two parties (and f2(x, y) is the respective second component of f(x, y) for the second party). The two-party protocol is denoted by Π.

denotes the view of the first party during an execution of Π on (x, y). Such a view consists of (x, r, m1,.., mt), where r represents the outcome of the first party?s internal coin tosses and mi represents the ith message it has received. Then, Π can privately compute f, with respect to the first party, if there exist a probabilistic polynomial time algorithm S1 such that even if party two provides arbitrary answers during the protocol, the corresponding view for the first party is the output of the algorithm S1 on the input x of the first party and the messages received by the first party. The protocol can privately compute f if it can do so with respect to both parties. The theory of this model [Gol98] shows that to compute privately under the semi-honest model is also equivalent to computing privately and securely. Therefore, the discussion of this model assumes parties behaving under the semi-honest model. In the following we explain what a public-key cryptosystem is

D. Public-key cryptosystems (asymmetric ciphers)

A cipher is an algorithm that is used to encrypt plaintext into cipher text and vice versa (decryption). Ciphers are said to be divided into two categories: private key and public key.

Private-key (symmetric key) algorithms require a sender to encrypt a plaintext with the key and the receiver to decrypt the cipher text with the key. A problem with this method is that both parties must have an identical key, and somehow the key must be delivered to the receiving party.

A public-key (asymmetric key) algorithm uses two separate keys: a public key and a private key. The public key is used to encrypt the data and only the private key can decrypt the data. A form of this type of encryption is called RSA (discussed below), and is widely used for secured websites that carry sensitive data such as username and passwords, and credit card numbers.

Public-key cryptosystems were invented in the late 1970s, along with developments in complexity theory [MvOV96, Sch96]. As a result, cryptosystems could be developed which would have two keys, a private key and a public key. With the public key, one could encrypt data, and decrypt them with the private key. Thus, the owner of the private key would be the only one who could decrypt the data, but anyone knowing the public key could send them a message in private. Many of the public key systems are also patented by private companies, which also limit their use. For example, the RSA algorithm was patented by MIT in 1983 in the United States of America as (U.S. patent #4,405,829). The patent expired on the 21st of September 2000.

The RSA algorithm was described in 1977 [RSA78] by Ron Rivest, Adi Shamir and Len Adleman at MIT; the letters RSA are the initials of their surnames. RSA is currently the most important public-key algorithm and the most commonly used. It can be used both for encryption and for digital signatures. RSA computation takes place with integers modulo n = p * q, for two large secret primes p and q. To encrypt a message m, it is exponentiated with a small public exponent e. For decryption, the recipient of the cipher text

computes the multiplicative reverse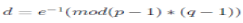

(we require that e is selected suitably for it to exist) and obtains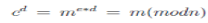

. The private key consists of n, p, q, e, d (where p and q can be forgotten); the public key contains only n, e. The problem for the attacker is that computing the reverse d of e is assumed to be no easier than factorising n [MvOV96].

The key size (the size of the modulus) should be greater than 1024 bits (i.e.it should be of magnitude 10300) for a reasonable margin of security. Keys of size, say, 2048 bits should give security for decades [Wie98].

Dramatic advances in factoring large integers would make RSA vulnerable, but other attacks against specific variants are also known. Good implementations use redundancy in order to avoid attacks using the multiplicative structure of the cipher text. RSA is vulnerable to chosen plain-text attacks and hardware and fault attacks. Also, important attacks against very small exponents exist, as well as against partially revealed factorization of the modulus.

The proper implementation of the RSA algorithm with redundancy is well explained in the PKCS standards (see definitions at RSA Laboratories [Sit]).The RSA algorithm should not be used in plain form. It is recommended that implementations follow the standard as this has also the additional benefit of inter-operability with most major protocols.

E. Yao’s millionaire protocol

Consider a scenario with two mutually distrusting parties, who want to reach some common goal, such as flip a common coin, or jointly compute some function on inputs that must be kept as private as possible. A classical example is Yao?s millionaire?s problem [Yao82]: two millionaires want to find out who is richer without revealing to each other how many millions they each own.

Yao?s protocol can be summarized in the following steps [ttMP]:

? Let I be Alice?s wealth (assuming the range is {1 . . . 10}).

? Let J be Bob?s wealth (assuming the range is {1 . . . 10}).

? Alice uses RSA, and has a public key which is (m, n), where m and n are integers. Her private key is k.

? Bob picks a random N-bit integer called X. Then Bob calculates C such that: C = Xm mod n, where C is the RSA encipherment of X.

? Bob takes C, and transmits to Alice C − J + 1.

? Alice generates a series of numbers Y 1, Y 2, Y 3 . . . Y 10 such that Y 1 is the RSA decipherment of (C − J + 1); Y 2 is the RSA decipherment of (C − J + 2); Y 3 is the decipherment of (C + J + 3); . . . ; Y 10 is the RSA decipherment of (C − J + 10). She can do this because although she does not know C or J, she does know (C − J + 1): it is the number Bob sent her.

? Alice now generates a random N/2 bit length prime p. Alice then generates Z1, Z2, Z3 . . . Z10 by calculating Y 1 mod p, Y 2 mod p, Y 3 mod p . . . Y 10 mod p. ? Alice now transmits the prime p to Bob, and then sends 10 numbers. The first few numbers are Z1, Z2, Z3 . . . up to the value of ZI, where I is Alice?s wealth in millions. So Alice sends Z1, Z2, Z3, Z4 and Z5. The rest of the numbers she adds 1 to, so she sends Z6 + 1, Z7 + 1, Z8 + 1, Z9 + 1 and Z10 + 1.

? Bob now looks at the Jth number where J is his wealth in millions, excluding the first prime. He also computes G = X mod p (X being his original random number and p being Alice?s random prime which she transmitted to him). Now, if the Jth number is equal to G, then Alice is equal to or greater than Bob in wealth (I ≥ J). If the Jth number is not equal to G, then Bob is wealthier than Alice (I < J).

? Bob tells Alice the result.

Let P = {P0, . . . , Pn} be a set of N parties where |N| ≥ 3. Each party Pi has a database DBi. We assume that parties running the protocol are semi-honest. The goal is to share the union of DBi as one shuffled database DBComp = Sn i=0 DBi and hide the link between records in DBComp and their owners.

Our protocol [ECH06] employs a public-key cryptosystem algorithm on horizontally partitioned data among three or more parties. In our protocol, the parties can share the union of their data without the need for an outside trusted party. The information that is hidden is what data records where in the possession of which party. Our protocol is described for one party as the protocol driver. We call this first party Alice.

1. Alice generates a public encryption key kPA. Alice makes kPA known to all parties (for illustration we use another two parties called Bob and Carol).

2. Each party (including Alice) encrypts its database DBi with Alice?s public key. This means the encryption is applied to each row (record or transaction) of the database. Parties will need to know the common length of rows in the database. We denote the result of this encryption as kPA(DBi) (refer to Figure 5.1). Note that, by the properties of public cryptosystems, only Alice can decrypt these databases.

3. Alice passes her encrypted transactions kPA(DB1) to Bob. Bob cannot learn Alice?s transactions since he does not know the decryption key (Fig. 5.2). 4. Bob mixes his transactions with Alice?s transactions. That is, he produces a random shuffle of kPA(DB1) and kPA(DB2) before passing all these shuffled transactions to Carol (see Figure 5.3).

5. Carol adds and shuffles her transactions kPA(DB3) to the transactions received from Bob. 6. The protocol continues in this way, each subsequent party receiving a database with the encrypted and shuffled transaction of all previous parties in the enumeration of the parties. The i-th party mixes randomly his encrypted transactions kPA(DBi) with the rest and passes the entries shuffled transaction to the (i + 1)-th party.

7. The last party (in our illustration Carol) passes the transactions back to Alice (see Figure 5.4).

8. Alice decrypts the complete set of transaction with her secret decrypt key. She can identify her own transactions. However, Alice is unable to link transactions with their owners because transactions are shuffled.

9. Alice publishes the transactions to all parties. If the number of parties is N, then N − 1 of the parties need to collude to associate data to their original owners (data suppliers).

IV. APPLICATION

It may seem that the protocol above is rather elaborate, for the seemingly simple task of bringing the data of all parties together while removing information about what record (transaction) was contributed by whom. We now show how to apply this protocol to improve on the privacy-preserving data mining of association rules.

The task of mining association rules over market basket data [AIS93] is considered a core knowledge discovery activity since it provides a useful mechanism for discovering correlations among items belonging to customer transactions in a market basket database. The association rule-mining problem was discussed in Section 3.1.

The distributed mining of association rules over horizontally partitioned data consists of sites (parties) with homogeneous schema for records that consists of transactions. Obviously we could use our protocol to bring all transactions to gather and then let each party apply an association-rule mining algorithm (Apriori or FP-tree, for example) to extract the association rules. This approach is reasonably secure for some settings, but parties may learn about some transactions with other parties. Ideally, it is desirable to obtain association rules with support and confidence over the entire joint database without any party inspecting other parties? transactions [KC04]. Computing association rules without disclosing individual transactions is possible if we can have some global information. For example, if one knows that 1) ABC is a global frequent item set, 2) the local support of AB and ABC and 3) the size of each database DBi, then one can determine if AB ⇒ C has the necessary support and confidence since sprt (AB ⇒ C) = PN i=1 Local Support at sitei(ABC) PN i=1 kDBik ,sprt (AB) = PN i=1 Local Support at sitei(AB) PN i=1 kDBik ,and confidence(AB ⇒ C) = sprt(AB ⇒ C) sprt(AB).

Thus, to compute distributed association rules privately, without releasing any individual transaction, the parties compute individually their frequent item sets at the desired support. Then, for all those item sets that are above the desired relative support, the parties use our protocol to share records that consist of the a local frequent item set, and its local support (that is, they do not share raw transactions). The parties also share the size of their local databases. Note that, we are sure that the algorithm finds all globally frequent item sets because an item set has global support above the global support at p percent only if at least one party has that item set as frequent in its database with local support at least p percent. We would like to emphasize two important aspect of our protocol in this application. The first is that we do not require commutative encryption. The second is that we require 2 fewer exchanges of encrypted data between the parties less than did the previous algorithms for this task. The third, is that we do not require that the parties find first the local frequent item sets of size 1 in order to find global frequent item sets of size 1, and then global candidate item sets of size two (and then repeatedly find local frequent item sets of size k in order to share them with others for obtaining global item sets of size k that can then formulate global candidate item set of size k + 1).

In our method, each party works locally finding all local frequent item sets of all sizes. They can use Yao?s Millionaire protocol to find the largest size for a frequent local item set. This party sets the value k and parties use our protocol to share all local and frequent item sets of size k. Once global frequent item sets of size k are known, parties can take precautions (using the anti-monotonic property that if an item set is frequent all its subsets must be frequent) so they do not disclose locally frequent item sets that have no chance of being globally frequent.

With this last aspect of our protocol, we improve the the privacy above previous algorithms [KC04].

The contribution here can be divided into: a) the overhead to the mining task is removed, and b) the sharing process was reduced from 6 steps to 4 steps as Figure 5 shows.

V. COST OF ENCRYPTION

In the past, parties who sought privacy were hesitant to implement database encryption because of the very high cost, complexity, and performance degradation. Recently, with the ever growing risk of data theft and emerging legislative requirements, parties are more willing to compromise efficiency for privacy. The theoretical analysis indicates that the computational complexity of RSA decryption of a single n bit block is approximately O(n3), where n denotes both the block length and key length (exponent and modulus). This is because the complexity of multiplication is O(n2), and the complexity of exponentiation is O(n) when square and multiply is used. The OpenSSL implementation can be used (with RSA keys) for secure, authenticated communication between different sites [Ope].SSL is short for Secure Sockets Layer, a protocol developed by Netscape for transmitting private data via the Internet. The overhead of SSL communication has been found of practical affordability by other researchers [APS99].

We analysed the cost of RSA encryption in terms of computation, number of messages, and total size. For this analysis, we implemented RSA in Java to calculate the encryption time of a message of size m = 64 bytes with encryption key of 1024-bits. This time was 0.001462 sec. on a 2.4MHz Pentium 4 under Windows. This is perfectly comparable with the practical computational cost suggested by earlier methods [KC04]. While some regard RSA as too slow for encrypting large volumes of data [Tan96], our implementation is particularly competitive. An evaluation of previous methods [KC04] suggested that (on distributed association rule mining parameters found in the literature [CNFF96]), the total overhead was approximately 800 seconds for databases with 1000 attributes and half a million transactions (on a 700MHz Pentium 3). Our implementation requires 30% of this time (i.e. 234.2 seconds), but on a Pentium 4. In any case, perfectly affordable.

We also performed another set of experiments to compare our protocol to the previous protocol [KC04]. We generated random data to create different database sizes from 2500 bytes to 2500000 bytes. The experiments included the whole steps of each protocol except for shuffling the records which is supposed to take the same amount of time in both of the protocols and thus can be ignored. In other words, the experiments included the encryption and decryption of different database sizes to compare the performance of our protocol to the other protocol. Figure 6 show that our protocol is significantly faster than the protocol in [KC04].

VI. SUMMARY AND CONCLUSION

We have proposed a flexible and easy-to-implement protocol for privacy-preserving data sharing based on a a public-key cryptosystem. The protocol is efficient in practical settings and it requires less machinery than previous approaches (where commutative encryption was required). This protocol ensures that no data can be linked to a specific user. The protocol allows users to conduct private mining analyses without loss of accuracy. Our protocol works under the common and realistic assumption that parties are semi-honest, or honest but curious, meaning they execute the protocol exactly as specified, but they may attempt to infer hid-den links and useful information about other parties. A privacy concern of this protocol is that the users get to see the actual data. But previous research has explored whether parties are willing to trade off the benefits and costs of sharing sensitive data [HHLP02, Wes99]. The results of this research showed that parties are willing to trade-off privacy concerns for economic benefits. There are several issues that may influence practical usage of the presented protocol. While the protocol is efficient, it may be still a heavy overhead for parties who want to share huge multimedia databases.

Figures at a glance


Figure 1	Figure 2	Figure 3


Figure 4	Figure 5	Figure 6

References

Agrawal, R., and Srikant (2007), „Privacy Preserving Data Mining?, Proceedings of the 19th ACM International Conference on Knowledge Discovery and Data Mining, Canada, pp. 439-450.
Agrawal D., and Aggarwal C.C (2007), „On the Design and Quantification of Privacy Preserving Data Mining Algorithms?, Proceedings of the 20th ACM Symposium on Principles of Database Systems, pp. 247-255.
Benjamin C. Fung M. and Ke Wang (2010), „Privacy-Preserving Data Publishing: A Survey of Recent Developments?, ACM Comput ing Surveys, Vol. 42, No. 4, pp.322-435.
Bertino E., Nai Fovino and Parasiliti Provenza (2005), „A Framework for Evaluating Privacy Preserving Data Mining Algorithms?, Journal of Data Mining and Knowledge Discovery, pp. 78-87.
Chris Clifton and Murat Kantarcioglu and Jaideep Vaidya (2002), „Defining Privacy for Data Mining’, Proceedings of the National Science Foundation Workshop on Next Generation Data Mining, pp.274-281.
Chris Clifton, Murat Kantarcioglu, Jaideep Vaidya (2004), „Tools for privacy preserving data mining?, Explorations Journal, volume 4, pages 28- 34.
Clifton C., Kantarcioglu, M. and Vaidya, J. (2008), „Defining Privacy For Data Mining’, Proceedings of the National Science Foundation Workshop on Next Generation Data Mining pp. 126-133.