ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Pratibha Srivastav1, Manoj Kumar Jha2, M.F. Qureshi3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper describes a design procedure for a Grey ANFIS based power system stabilizer (GrANFISPSS) and investigates their robustness for a multi-machine power system. Speed deviation of a machine and its derivative are chosen as the input signals to the GrANFIS-PSS. A four-machine and a two-area power system is used as the case study. Computer simulations for the test system subjected to transient disturbances i.e. a three phase fault, were carried out and the results showed that the proposed controller is able to prove its effectiveness and improve the system damping when compared to a conventional lead-lag based power system stabilizer controller. The simulation result shows that the GrANFIS-PSS can be designed to achieve good performance merely using the combination of Grey prediction and Adaptive Neuro-Fuzzy Inference System (ANFIS). GrANFIS-PSS is designed to damp out the low frequency local and inter-area oscillations of the Multi-machine power system. By applying this GrANFIS-PSS to the power system the damping of inter-area modes of oscillations in a multi-machine power system is handled properly. The effectiveness of the proposed GrANFIS-PSS is demonstrated on two area four machine power system (Kundur system), which has provided a comprehensive evaluation of the learning control performance. Finally, several fault and load disturbance simulation results are presented to stress the effectiveness of the proposed GrANFIS-PSS in a multimachine power system and show that the proposed intelligent controls improve the dynamic performance of the GrANFIS-PSS and the associated power network
Keywords |
| Grey Prediction, Power system oscillations, linear models, ANFIS |
INTRODUCTION |
| Power system oscillations occur due to the lack of damping torque at the generators rotors. The oscillation of the generators rotors cause the oscillation of other power system variables (bus voltage, bus frequency, transmission lines active and reactive powers). Power system oscillations are usually in the range between 0.1 and 2 Hz depending on the number of generators involved. Local oscillations lie in the upper part of that range and consist of the oscillation of a single generator or a group of generators against the rest of the system. In contrast, inter-area oscillations are in the lower part of the frequency range and comprise the oscillations among groups of generators. |
| To improve the damping of oscillations in power system, a Power System Stabilizers (PSSs) applied on selected generators can effectively damp local oscillation modes while for inter-area oscillations a supplementary controller can be applied. Most of these controllers are designed base on conventional approach that is designed based on a Linearized model which cannot provide satisfactory performance over a wide range of operation points and under large disturbances. Neural networks, enjoy a variety of advantages (e.g., high speed, generalization capability and learning ability), are a viable choice for non-linear control design. |
| It has been successfully applied to the identification and control of dynamical systems especially in the field of adaptive control by making use of on-line training. Direct and indirect adaptive control with MLP and RBF neural networks has been discussed for such systems which rely on continuous online training of the identifier and controller network. It presents single-neuron and multi-neuron Radial Basis Function Controller (RBFNN) for the UPFC control in single machine-infinite-bus and three-machine power systems and claimed to provide the best transient stability performance of the power system. This is because output layer of RBF can be optimized fully using traditional linear modeling techniques but, before linear optimization can be applied to the output layer of an RBF network, the number of radial units must be decided and then their centers and deviations must be set. The use of Neuro-fuzzy to aid in controlling power oscillation damping in large power system has been studied for some years by several researchers. In this paper, the implementation of GrANFIS-PSS for Multi-machine power system has been described. Initial values of membership functions and rule base of the ANFIS have been obtained using the knowledge of dynamic behavior of the power devices in multi-machine power system, then membership functions’ values have been optimized by the ANFIS. The performance of the GrANFIS-PSS with the conventional controller for a number of operating conditions has been compared. |
| Low frequency oscillations occur in power systems due to disturbances. If no adequate damping is available, such oscillations can increase and cause system separation. Power system stabilizers (PSS) are installed in power systems generators to enhance damping and provide supplementary feedback stabilizing signals which extend the power stability limits. Under the conventional PSSs, the proposed eigen value assignment technique is iterative and leads to heavy computations, which give rise to time-consuming computer codes. Furthermore, the initialization step is crucial and affects the final dynamic response of the controlled system. From a given set of eigen values, different designs can be obtained by simply altering the parameters involved in the initialization step. Mathematical programming techniques have been applied to assist in the final criteria of these conventional PSSs; however, they disregard conservativeness and cause the number of constraints to increase considerably. The optimization process requires the computations of sensitivity factors and eigen-factors at each iteration. This results in heavy computational tasks and slow convergence. The search process will somehow be trapped in local minima and the solution obtained will not be optimal. |
| As far as modern control theory is concerned, several approaches have been proposed to improve the PSS design problem; these include optimal control, adaptive control, variable structure control and intelligent control. The present paper introduces a power stabilizer based on Grey Prediction and ANFIS design controllers. The influence of the proposed GrANFIS-PSS design on the dynamic characteristics of the controlled system is investigated. Simulation results to illustrate the effectiveness of the proposed controller are presented. These results have been obtained from a simulation study on a four-machine power network. In this study, the system has been subjected to a severe type of disturbance, i.e. a sudden three-phase short circuit fault at the end of one of the system busbars. This test demonstrates the enhancement of the transient stability of the system. In this GrANFIS-PSS based design, a rule was extracted from a conventional controller to give an initial solution. A speed deviation and its derivative are used as an input to the GrANFIS-PSS. The ANFIS is used as a second design method. Training data are taken from the output of a conventional controller and are fed to ANFIS for training. The proposed design approaches are applied to a 4 machine two-area power system. Different size of an input/output membership function and defuzzification methods are used to assess the effectiveness of the proposed controller in terms of damping out the electromechanical modes of oscillation. |
II. GREY MODEL |
GM (1,1) Model |
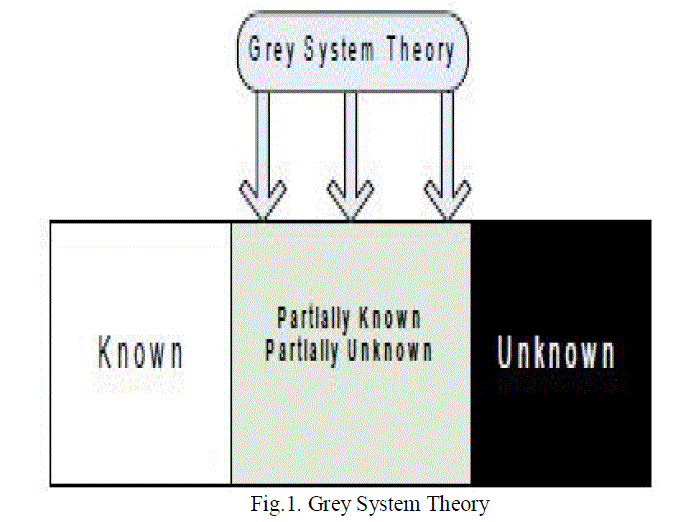
| Grey system theory introduced by Deng (1989) is pretty much similar to FL in nature thought it’s completely crisp. The theory also; like FL, is comparatively new. The grey system theory (Fig.1) can simply be summarized as a methodology that concerns with the systems comprising uncertainties and lack of sufficient amount of information in which, the term ‘grey’ indicates the system information that lays between the clearly and certainly known ones (the white part) and the unknown ones which contains any knowledge of the system structure (the black part); so that grey systems include partially known and partially unknown characteristics. Differently from statistical forecasting methods which usually needs large past periods data sets to have better regularity of variables of random process, grey theory uses accumulated generating operation (AGO) to obtain regularity via which noise is reduced by converting ambiguous original time series data to a monotonically increased series(See Fig.2). |
 |
| The importance of AGO in grey system theory arise from its capability of turning unimproved stochastic data to useful regulars series and inverse accumulated generic operation (IAGO); which is the other important tool of grey system theory, transforms this AGO generated regulars series to row data sequence. The basic idea of the grey model is to construct a regular differential equation with the help of AGO which denoted in general form as GM (n, m) of where, n denotes the order of ordinary differential equation and m denotes the number of grey variable defining the order of AGO and IAGO. As increases in n and m also increases the computation time exponentially causing likely correctness defects, most widely use model in grey system theory is GM (1, 1) which has important advantages those can be summarized as the usage for any kind of data distribution including small data sets and less requirement for computation. |
| In order to smooth the randomness, the primitive data obtained from the system to form the GM (1, 1) is subjected to an operator, named Accumulating Generation Operation (AGO). The differential equation (i.e. GM (1, 1)) thus evolved is solved to obtain the n-step ahead predicted value of the system. Finally, using the predicted value, the inverse accumulating operation (IAGO) is applied to find the predicted values of original data. Consider a single input and single output system. Assume that the time sequence X(0) represents the outputs of the system: |
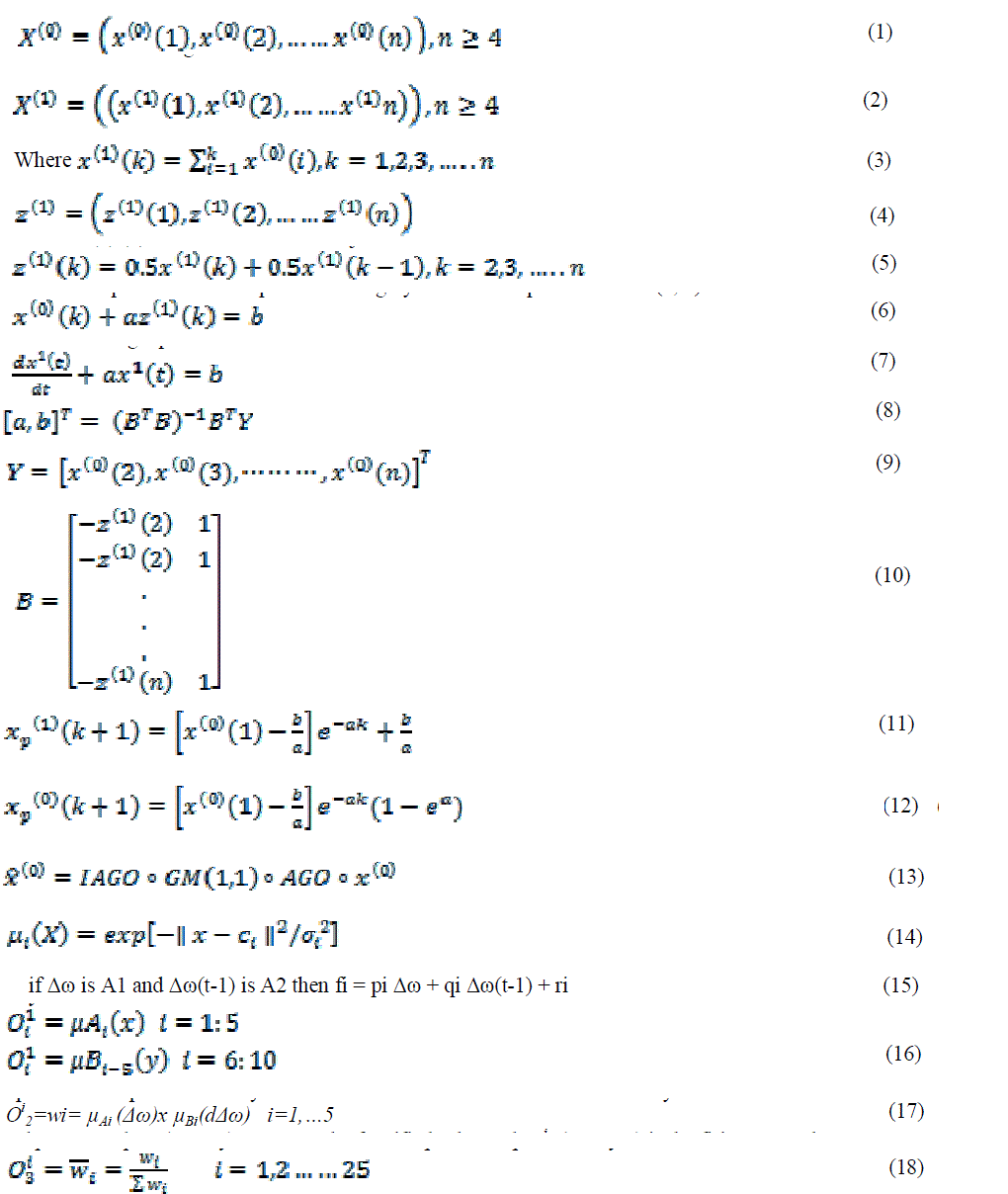 |
 |
 |
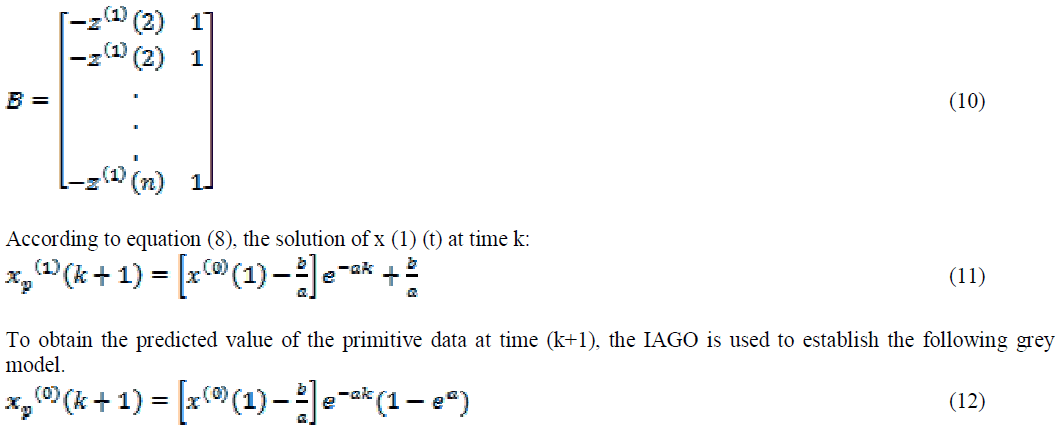 |
| The parameter (α) in the GM (1, 1) model is called “development coefficient” which reflects the development states of X(1)p and X(0)p . The parameter b is called “grey action quantity” which reflects changes contained in the data because of being derived from the background values. Based on the above description, the grey predictor composed of AGO, IAGO and GM (1,1) can be constructed by Fig.2 shows the Grey process. |
 |
| Since the GM (1,1) model owns nonlinear predictive character under a few data samples (at least 4 points) as well as neural network has memory function, we present a grey-neural model compensator approach in this study. The past data x(t-k),....x(t −1), x(t) are used to establish the GM(1,1) model and a threshold value is used to decide whether the signal [x(t −k),....x(t −1), x(t); x(t+γ)] is a kind of anomalous condition or not. Namely, if the forecasting error is larger than the threshold value, then the [x(t −k),....x(t −1), x(t); x(t+γ) are transferred to neural network .The GM(1,1) is primary predictor, while the neural tuner analyzes the data. If there is an improper condition, the neural network residual error will appropriately modify the predictive data. |
Structure of GrANFIS-PSS |
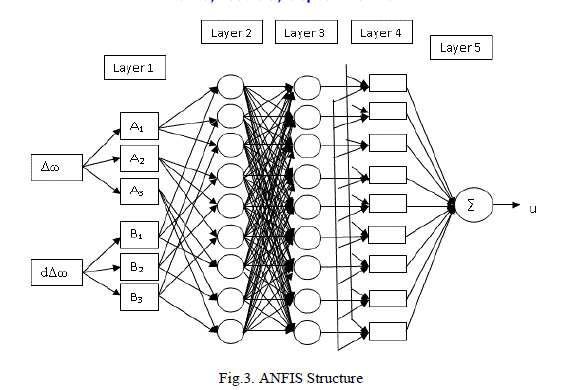
| The fuzzy inference systems for this system is a two input and one output first-order Takagi and Sugeno’s fuzzy if-then rules and are used in the GrANFIS-PSS architecture with twenty five rules whose block diagram is illustrated here in Fig.2. The input to the GrANFIS-PSS is the speed deviation and change of speed deviation. The linguistic rules, considering the dependence of the plant output on the controlling signal, are used to build the initial fuzzy inference structure. The inputs scaling blocks maps the real input to the normalized input space in which the membership functions are defined. The output scaling block is used to map the output of the fuzzy inference system to the real output needed. The inputs signals are fuzzified using five fuzzy sets Ai and Bi, i=1 to 5. Any continuous and piecewise differentiable functions are qualified candidates for node functions of premise parameters of the ANFIS structure. This work considers the Gaussian function as the initial fuzzy membership function, with maximum equal to 1 and minimum equal to 0 and is given by |
 |
| Where ci is the center vector of the function, which has same dimension as input vector,σi is a specific parameter of the Gaussian function, and the Gaussian function μi has the only max value at the center ci. The initial values of premise parameters are set in such a way that the MF’s are equally spaced in the range [-1 1]. The outputs of the inference system are linear membership functions and the rule base with five fuzzy if-then rules of (TS) Takagi and Sugeno’s type given by |
| if Δω is A1 and Δω(t-1) is A2 then fi = pi Δω + qi Δω(t-1) + ri (15) |
| Where Δω and Δω(t-1) are the inputs of the systems while A1 and A2 are fuzzy sets in the antecedent, and pi, qi and ri are the consequent parameters. |
III.ANFIS TRAINING |
| The steps for ANFIS training to adapt the initial fuzzy premise parameters for construction of the proposed optimum input output pattern to perform the desired control action at various operating conditions is presented. ANFIS uses a hybrid learning algorithm to recognize consequent parameters of Sugeno-type fuzzy inference systems. It applies a combination of the least squares method and Back propagation gradient descent method for training fuzzy inference system membership function parameters to follow a given training data set. The neuro-fuzzy system owes much from the feed forward neural network with supervised learning capability. The output of the fuzzy system for approximation of premise parameter set [ ci, σi] is trained by the ANFIS in five layers of networks , the node functions are as follows: |
 |
 |
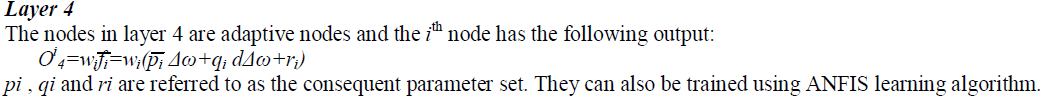 |
Layer 5 |
| Layer 5 is a fixed node with function of summation which computes the overall output ‘u’as the summations of all incoming signals Fig.3 show a 2-input, ANFIS with 25 rules. Five membership functions are associated with each input, so the input space is partitioned into twenty five fuzzy subspaces, each of which is governed by fuzzy if-then rules. The premise part of a rule delineates a fuzzy subspace, while the consequent part specifies the output within this fuzzy subspace. The choice of learning algorithm is based on trade-off between computation complexity and resulting performance. The learning method adopted in this work is the hybrid learning rule that combines the least-squares estimator and the gradient descent method. This hybrid learning technique speeds up the learning process compared to the gradient method alone, which exhibits the tendency to become trapped in local minimum. |
IV. TRAINING PHASE OF GRANFIS-PSS |
| The training data is obtained by simulating a power system that is subjected to a wide range of possible disturbances. The rotor speed output and its derivatives are used as training data that are Δω and dΔω and the control action data ‘u’ as input to the model are obtained by simulating the system under the above conditions. The training data are arranged in this form [Δω, dΔω,u ]. |
Design of Grey ANFIS based power system stabilizer (GrANFIS-PSS) |
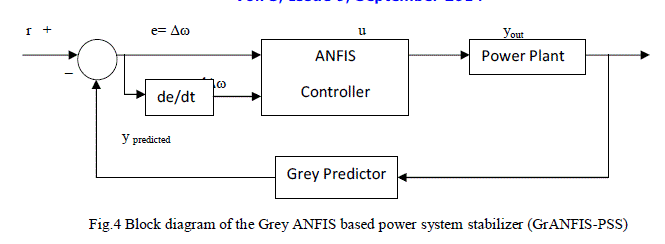
| In grey systems theory, prediction error is used instead of current measured error. In similar lines, during the development of the Grey ANFIS based power system stabilizer (GrANFIS-PSS), the prediction error is considered as the error of the system. The block diagram of the Grey ANFIS based power system stabilizer (GrANFIS-PSS) is proposed in this paper is showed in Fig.4. |
 |
| In order to adapt the forecasting different states of the controller changing with error and the derivative of the error, another fuzzy controller is designed. The inputs of this ANFIS controller are e and eÃâ¹Ãâ¢. The output y out. Triangle membership functions are used for fuzzification process. |
| The fuzzy variables e and eÃâ¹Ã⢠are partitioned into 5 subsets (NL, NS, ZR, PS, PL) and the output variable y out is partitioned into 5 subsets (VS, S, MD, B, VB). The range of e, eÃâ¹Ã⢠and u is considered as [-0.5;2], [-0.07;0.07] and [0;80], respectively. |
| Physical domains can be calculated from the generated data for simulation by the conventional controllers; one installed between bus 5 and bus 7 and another between bus 6 and bus 9 respectively. For the rule-base, the relationship between the fuzzy controller inputs and its output can be extracted from the following algorithm: |
 |
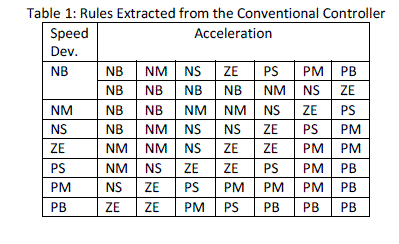 |
| In MATLAB, the ANFIS editor graphics user interface is available in Fuzzy Logic Toolbox Using a given input/output data set, the toolbox constructs a fuzzy inference system (FIS) whose membership function parameters are adjusted using either a back-propagation algorithm alone, or in a combination with a least squares type of method. This allows the fuzzy systems to learn from the data Power System Damping Using GrANFIS-PSS they are modeling. For the back-propagation-based neuro-fuzzy approach, it includes the Sugeno’s model with the following format: |
| If speed deviation error is Δω and the acceleration is dΔω ithe Upss is |
| Upss=pi Δω+qi dΔω+ri |
| where, i ={1, n*m} refers to the rule numbers, j ={1, n} refers to the Speed Deviation Error terms in the fuzzy set, n, m refers to the number of terms generated, k ={1, m} refers to the acceleration terms in the fuzzy set, pi ,qi , ri are the ith consequent (PSS output) parameters. The input signals to the GrANFIS-PSS controller for the PSS are Δω and dΔω |
V. SIMULATION STUDIES |
Input torque reference step change |
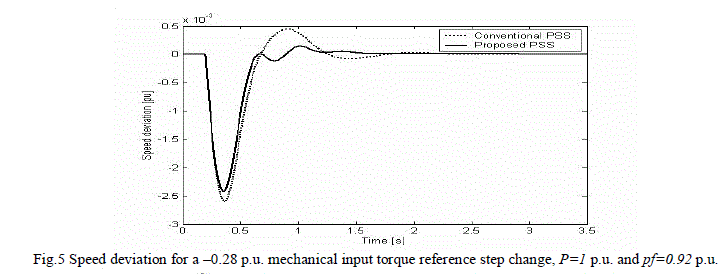
| With the generator operating at an active power of 1 p.u. and power factor lag of 0.92, a 25% step decrease in the input torque reference was applied at t=0.18 s. The speed deviation of the generator for the proposed PSS and the conventional PSS are shown in Fig.5. With the selected PSS parameters, the CPSS and the proposed PSS responses were very close to each other. |
 |
| Changing the operating point to 0.65 p.u. generated power and a power factor lead of 0.84, a 25 % step decrease in input torque reference was applied at t=0.18 s. The speed deviation for the proposed PSS and the conventional PSS are shown in Fig. 6. The proposed PSS shows better damping |
Switching of one line |
| At an operating point of 0.88 p.u., 0.95 power factor lag, one circuit of the double circuit transmission line was switched off at t=8 s. Before the line disconnection, 0.18 p.u. step increase |
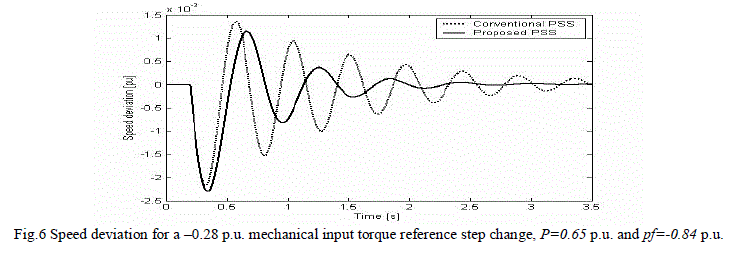 |
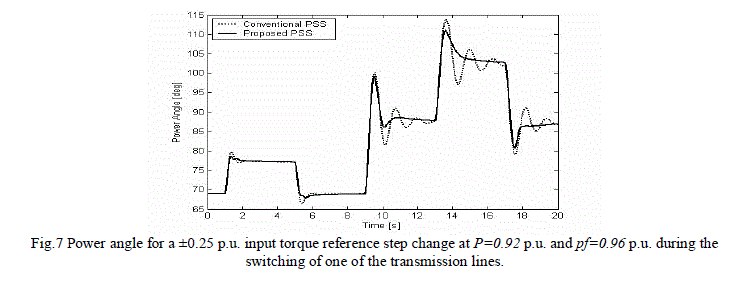
| in the input torque reference was applied at t=.88 s and removed at t=4.8 s. A second 0.25 p.u. step increase in the input torque reference was applied at t=12 s. and removed at t=15 s. during the transmission line fault. The response of the system with both conventional PSS and the proposed PSS is shown in Fig. 7. The response with the proposed PSS shows fewer oscillations than the conventional PSS and demonstrates better performance. |
Three phase to ground fault |
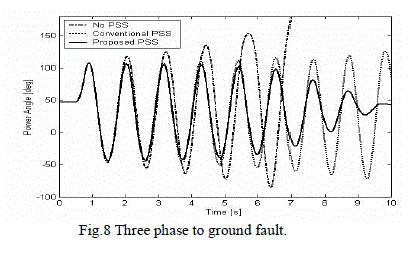
| Three phase to ground fault locating at 60 % of the distance along line is applied at t=0.55 s. and the fault is cleared at t=0.758 s. Responses without stabilizer and with conventional PSS and. |
 |
| Proposed PSS are shown in Fig.8. Systems without stabilizer and with conventional PSS are both unstable. The system with proposed GrANFIS-PSS is highly oscillatory, but it is stable. |
Robustness Test with changing shapes and number of Membership Functions |
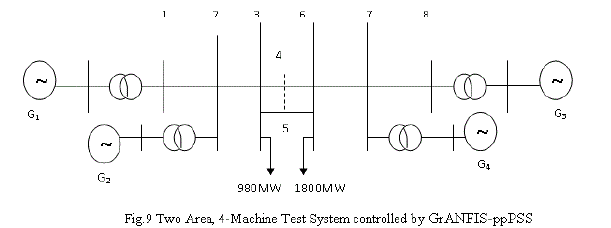
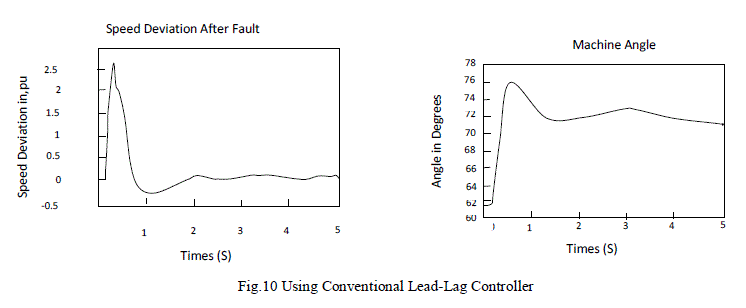
| The single-line diagram of the two-area, 4-machine test system, as shown in Fig.9, is used to examine both local and inter-area oscillations control problems. This system is created especially for the analysis and study of the inter-area oscillation problem. As shown in the above single-line diagram there are four generators, G.1 and G.2 for area-1, G.3 and G.4 for area-2, and four 20/240 kV step-up transformers. There are two loads in the system at buses 3 and 13. This system exhibits three electromechanical modes of oscillations where one inter-area mode of the generating units in one area oscillates against those in the other area. The frequency of this mode varies from 0.45 to 0.85 Hz depending on the operating conditions. Two local modes represent oscillations between the generating units within each area. The frequency of the local modes is around 1.8 Hz and the loads are modeled as constant impedances. One set of GrANFISPSS controllers is used for generator number one and one conventional-PSS for generator number two. In order to test the robustness of the proposed design procedure of GrANFIS-PSS, an experiment was carried-out for a three-phase to ground fault at the middle of one transmission line between busses 3 and 13, which is cleared after 0.07 seconds by tripping the fault-line. |
 |
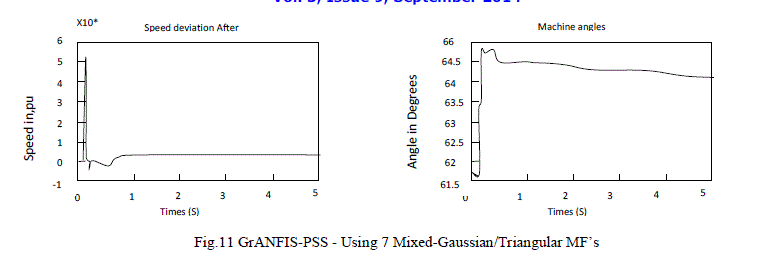
| The results show that the oscillations are damped more effectively when the GrANFIS-PSS is used. From all the results shown in Fig.10 to Fig.15, it can be seen that the mixed-Gaussian/ Triangular MF gives the best results compared with the others. Here best means reaching the steady state condition in the shortest time and with a minimum deviation. By using the MOM defuzzification method, (see in Fig.12), the controller settles at zero as the rules move abruptly from each cell to cell. This is expected since the MOM is more suited for decision making problems. |
 |
 |
 |
VI. CONCLUSION |
| In this study, GrANFIS-PSS is proposed for damping oscillations and the effectiveness of the proposed control system is compared with Conventional controller under some disturbances. The controller is tested on a well known bench mark power system model proposed by Kundur called two area four machines system. From the results it can be concluded that the GrANFIS-PSS produces no steady state error and acceptable overshoot under some disturbances. The work in this research involves a design of GrANFIS-PSS, which is built based on the data generated by the conventional controller. The generation of fuzzy rule-based and input-output domain ranges has been investigated. It has been found that the GrANFIS-PSS provides more robust control against severes disturbances with quicker settlingtimes when compared with a conventional lead-lag stabilizer. |
References |
|