ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Subhashini.V1, Babu.M2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The domain name auction facilitates the buying and selling of currently registered domain names, enabling individuals to purchase a previously registered domain that suits their needs from an owner wishing to sell. Domain auction sites allow users to search multiple domain names that are listed for sale by owner, and to place bids on the names they want to purchase. As in any auction, the highest bidder wins. The more desirable a domain name, the higher the winning bid, and auction sites often provide links to escrow agents to facilitate the safe transfer of funds and domain properties between the auctioning parties.
Keywords |
| Async MQ, bid, Model checker,Equilibrium approaches |
INTRODUCTION |
| Auctions are used to determine how billions of dollars of goods and services will be allocated across the globe. Each bidder privately sends a bid to the auction. A common objective among all of these auctions is to allocate the item to the bidder. Who values the item the most (that is, to allocate the item efficiently). The differences among them mostly reflect other issues. a bidder may not have to invest the effort necessary to determine her exact valuation for the item. The winner no longer has to think about how much longer she would have stayed in the auction domain the winner no longer has to think about how much longer she would have stayed in the auction. In the first-price auction, bidders will try to only slightly outbid their competitors, to pay as little as possible. If the bidder with the highest valuation for the item underestimates the other bids, this can result in another bidder winning the item, so that the allocation is inefficient. In the second-price sealed-bid auction, however, there is no reason to try to only slightly outbidthe next bidder; in fact, it can be shown that it is optimal to bid one’s true valuation for the item. The various auctions agree, in some sense, on the objective of efficient allocation, and the differences merely reflect other issues. There are other auctions that have a different objective, such as revenue-maximizing auctions, which do not always allocate the item efficiently. As in the single-item auction case, there are distinctions among combinatorial auctions in terms of the temporal aspects of the auction as well as the payments to be made by the bidders. |
| A primary principle of market design is to promote an efficient outcome to the extent possible. For the case addressed here with independent valuations for a single domain, this requires a design to enable the bidder who most values a domain to win it. |
| The problem of valuation and information feedback has been addressed by proposing two new combinatorial auction schemes,RevalSlotand RevalBundle. These two schemes allow the bidders to participate in the auctionwithout imposing the requirement that bidders have an accurate idea of their valuations. RevalSlotuses the concept of varying slot sizes to guide the bidders in their bidding. Equilibrium bidding strategies in sealed-bid auctions for two payment rules, the first-price rule in which the winner pays her bid, and the second-price rule in which the winner pays the second-highest bid. We characterize equilibrium bidding strategies and predicted outcomes for both asymmetric and symmetric distributions of the bidders’ valuations, assuming in each case that all bidders have the same interval of possible valuations over which the probability densities of their valuations is positive. The high participation and monitoring costs of bidders in online combinatorial auctions has been addressed by proposing a distributed signal driven combinatorial auction scheme. |
| A. Domain Name Auction |
| A number of factors have contributed to the rise in popularity of the domain name auction. The personalization of the web resulted in domain names being purchased by more private individuals and businesses than originally anticipated; and as a result there was also a rise in speculation and domain name warehousing. Anticipating a growing need for a targeted top-level domain name, domineers began to purchase names with an eye towards selling them at a later time. The advancing field of Search Engine Optimization (SEO) has also increased the desire to own a domain name that accurately reflects the subject matter of the web site. |
| A domain auction website provides the technology through which users can list or purchase multiple domains easily and conveniently. Domain parking, once the most efficient method for advertising a domain for sale, allowed a domain owner to post the availability of the domain on a page, hoping someone who was interested in that name would surf through and see it listed for sale. With the development of the domain auction, multiple users can list multiple domains all in the same place, thereby exposing them to a greater number of potential buyers. Sites such as eBay have made using auctions very commonplace, and domain auction sites also require little to no technical knowledge to use. |
| In the past, if a domain name was already registered by another party, it was generally advisable to choose a different name. Whether current owners list domains for auction for a specified period of time or provide an instant purchase option, the domain auction has become an important tool in uniting buyers and sellers in the quest for the most beneficial domain name. |
MODEL CHECKER |
| Model of a system, exhaustively and automatically check whether this model meets a given specification. Typically, one has hardware or software systems in mind, similar critical states that can cause the system to crash. Model checking is a technique for automatically verifying correctness properties of finitestate systems. |
| In order to solve such a problem algorithmically, both the model of the system and the specification are formulated in some precise mathematical language: To this end, it is formulated as a task in logic, namely to check whether a given structure satisfies a given logical formula. The concept is general and applies to all kinds of logics and suitable structures. A simple modelchecking problem is verifying whether a given formula in the propositional logic is satisfied by a given structure. Model checking is a method for formally verifying finite-state concurrent systems. Specifications about the system are expressed as temporal logic formulas, and efficient symbolic algorithms are used to traverse the model defined by the system and check if the specification holds or not. Extremely large state-spaces can often be traversed in minutes. |
| Property checking is used for verification instead of equivalence checking when two descriptions are not functionally equivalent. Particularly, during refinement, the specification is complemented with the details that are unnecessary in the higher level specification. Yet, there is no need to verify the newly introduced properties against the original specification. It is not even possible. Therefore, the strict bi-directional equivalence check is relaxed to one-way property checking. The implementation or design is regarded a model of the circuit whereas the specifications are properties that the model must satisfy. An important class of model checking methods have been developed for checking models of hardware and software designs where the specification is given by a temporal logic formula. Model checking is most often applied to hardware designs. For software, because of undecidability the approach cannot be fully algorithmic; typically it may fail to prove or disprove a given property. |
| The structure is usually given as a source code description in an industrial hardware description language or a special-purpose language. Such a program corresponds to a finite state machine (FSM), i.e., a directed graph consisting of nodes (or vertices) and edges. A set of atomic propositions is associated with each node, typically stating which memory elements are one. The nodes represent states of a system, the edges represent possible transitions which may alter the state, while the atomic propositions represent the basic properties that hold at a point of execution. Formally, the problem can be stated as follows: given a desired property, expressed as a temporal logic formula p, and a structure M with initial states, decide If M is finite, as it is in hardware, model checking reduces to a graph search. |
EQUILIBRIUM BIDDING |
| Equilibrium bidding strategies in sealed-bid auctions for two payment rules, the first-price rule in which the winner pays her bid, and the second-price rule in which the winner pays the second-highest bid. We characterize equilibrium bidding strategies and predicted outcomes for both asymmetric and symmetric distributions of the bidders’ valuations, assuming in each case that all bidders have the same interval of possible valuations over which the probability densities of their valuations is positive. First-price sealed-bid auctions in which bidders place their bid in a sealed envelope and simultaneously hand them to the auctioneer. The envelopes are opened and the individual with the highest bid wins, paying the amount bid. A first-price sealed-bid auction is a form of auction where bidders submit one bid in a concealed fashion. The submitted bids are then compared and the person with the highest bid wins the award, and pays the amount of his bid to the seller. This differs from a standard English auction in that bids are not open or called; bidders must submit valuations based upon supposed market value and their own willingness to pay — as opposed to engaging in competition through relative prices with other bidders. Other forms of auction include the Vickrey auction, or second priceauction, where the highest bidder wins but pays only the secondhighest bid. |
| A. Asymmetric Bidders |
| A first-price auction in which individual domains or batches of domains are sold sequentially, and a simultaneous second-price auction in which all domains are sold simultaneously. In the sequential auction each domain is auctioned in sequence in a sealed-bid first-price auction. The high bidder wins the domain and pays its bid to the losing bidders, with the total payment divided equally among them. |
| 1.The auction selects an allocation that maximizes the total reported values of all bidders. |
| 2. The difference between the payment a bidder would owe given any two, different bids is equal to the effect of the resulting change in allocation (if any) on all other bidders’ reported values. |
INDEPENDENT PRIVATE VALUE |
| Bidder has a privately known valuation that is independently distributed according to the probability distribution with cumulative and positive density on an interval that is the same for all bidders. In a monotone pure-strategy equilibrium, bidder bids if her value is . Assume throughout that the bidding strategy is an increasing and differentiable function, and thus has an increasing and differentiable inverse function . That is, bidder bids when her valuation is vi=ai(b). |
| The lines between content and the deep Web have buyer and Sellers as search services start to provide access to part or all of once-restricted content. An increasing amount of deep Web content is opening up to free search as publishers and libraries make agreements with large databases. |
| After each auction, the auction system reports the high bid. The auction system also presents to each participant its own current winnings and its current settlement balance, which reflects payments for the domains it wins and receipts for domains it lost. The auction schedule is also displayed. For practical reasons, sets of domains may be grouped into batches which are sold. |
| 1) The bidders are risk neutral, in the sense that they try to maximize their expected profits and their bids avoid any situation that might give them negative payoffs. |
| 2) The valuations of bidders follow the independent private values model (see the section on valuation issues below) |
| 3) The bidders are symmetric (that is all of them draw theirvaluations from the same probability distribution) 4) Payments or prices depend only on bids |
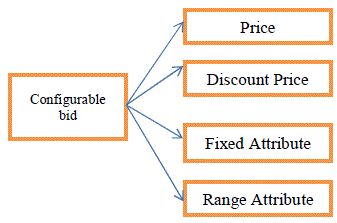 |
| The System does not have a prior knowledge of the Priority Model checker and the bid rating on the other hand is not aware of the actual data that is being facilitates by buyer and seller. |
| 1) Watch list - To watch the list of domains |
| 2) Auction Rating- To Maintain the Domain Rating List |
| 3) Contact Seller - Add and Edit the Contact Seller Details. |
| 4) User rating - To view the user rating |
 |
BIDDING TOOL |
| The auction system, you will have a bidding tool, applicant -auction-tool-sequential.xlsx. All bidders have the same tool. The tool allows you to explore alternative bidding strategies. It includes all the information that is common knowledge: the domains, the bidders and which domains each can bid for, the equilibrium bid functions wherever the equilibrium is known. Note that there is a separate sheet for each auction. Be sure you are using the correct sheet for the particular auction. |
| To use the tool, you will need to go to the appropriate sheet. Each of the two auctions has a separate sheet Symmetric1 and Symmetric2. Then sort the sheet by your bidder name and then by domain, so that all the domains you can bid for are listed first and in alphabetical order. Then you can paste your values into the sheet from the auction system by clicking on the Bidder Info button, selecting all domains and values in the window toward the bottom of the screen, then Ctrl-C to copy. Of course this step must be repeated for each auction. Be sure to save the Workbook once your values are pasted in. Also save your workbook at the end of each auction. |
| Profit from domain won: |
| profitwon = value-price |
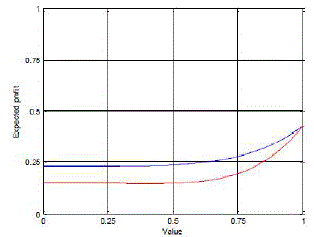 |
| Both auction designs were implemented in software, using a state of the art commercial web-based auction framework. The user interface was custom written for the auction designs proposed, to allow experiment subjects to focus on the auction. In both cases, subjects were able to enter proxy bids, and the software kept track of the bidder’s values to simplify the bidding process and eliminate sources of errors by the bidders |
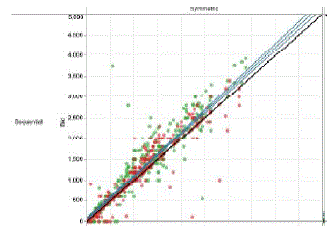 |
DESIGN AUCTION |
| The Design Auction together buyers and sellers in commerce-oriented settings, but do not enable negotiation transactions.Some EMs facilitate all transactions, including after-sales service. A number of EMs offer secondary transactions and others, again, have outsourced them. The more the transaction phases that are supported and the more non-buying/ non selling transactions that are in addition possible, the more opportunities for information sharing and collaboration there will be. Some innovative EMs have broadened their service by providing additional services such as facilitating collaboration in product development or order management. |
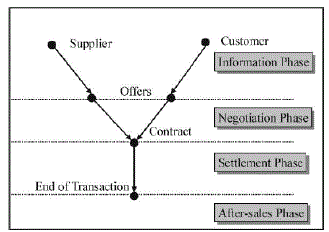 |
CONCLUSION |
| This Domain auction system can be implemented with model checker . In addition it can be enhanced for future work for Averset framework through symbolic model checker. Instead of enumerating reachable states one at a time, the state space can sometimes be traversed much more efficiently by considering large numbers of states at a single step. When such state space traversal is based on representations of states sets and transition relations as formulas, binary decision diagrams or other related data structures, the model-checking method is symbolic. |
References |
|