Keywords
|
| Hydrostatic initial stress, Three-phase-lag, Thermoelastic, Thermodynamic temperature, Conductive temperature, Normal-mode. |
INTRODUCTION
|
| The generalized theory of thermoelasticity is one of the modified versions of classical uncoupled and coupled theory of thermoelasticity and has been developed in order to remove the paradox of physical impossible phenomena of infinite velocity of thermal signals in the classical coupled thermoelasticity. Five generalizations of the coupled theory of thermoelasticity have investigated [1]. The first generalization formulates the generalized thermoelasticity theory involving one thermal relaxation time [2]. The temperature rate-dependent thermo-elasticity is developed where includes two thermal relaxation times and does not violate the classical Fourier’s law of heat conduction, when the body under consideration has a center of symmetry [3]. One can review and presentation of generalized theories of thermoelasticity [4]. The wave propagation in anisotropic solids in generalized theories of thermoelasticity has studied [5-7]. The third generalization of the coupled theory of thermoelasticity is developed by Hetnarski and Ignaczak and is known as low-temperature thermoelasticity. The fourth generalization to the coupled theory of thermoelasticity introduced by Green and Naghdi and this theory is concerned with the thermoelasticity theory without energy dissipation, referred to as G-N theory of type II in which the classical Fourier law is replaced by a heat flux ratetemperature gradient relation and Green and Naghdi with energy dissipation referred to as G-N theory of type III. The fifth generalization of the coupled theory of thermoelasticity is referred to the dual-phase-lag thermoelasticity [8, 9]. Recently the three-phase-lag, heat conduction equation in which the Fourier law of heat conduction is replaced by an approximation to a modification of the Fourier law with the introduction of three different phases-lags for the heat flux vector, the temperature gradient and the thermal displacement gradient [10]. The stability of the three-phase-lag, the heat conduction equation is discussed [11]. Subsequently, this theory has employed of thermoelasticity with threephase- lag to discuss a problem of thermoelastic interactions on functional graded orthotropic hollow sphere under thermal shock [12]. |
| Some researchers in the past have investigated different problems of rotating media. The propagation of plane harmonic waves in a rotating elastic medium without a thermal field has been studied [13]. It was shown there that the rotation causes the elastic medium to be depressive and anisotropic. An investigation of the distribution of deformation, stresses and magnetic field in a uniformly rotating, homogeneous, isotropic, thermally and electrically conducting elastic half-space was presented [14]. The effect of rotation on elastic waves has been studied [15, 16]. The effect of rotation in a magneto-thermoelastic medium was discussed [17]. |
| The two-temperature theory of thermoelasticity was introduced [18-20], in which the classical Clausius-Duhem inequality was replaced by another one depending on two-temperature; the conductive temperature and the thermodynamic temperature, the first is due to the thermal processes, and the second is due to the mechanical processes inherent between the particles and the layers of elastic material, this theory was also investigated [21]. The two-temperature model was underrated and unnoticed for many years thereafter. Only in the last decade the theory has been noticed, developed in many works, and find its applications, mainly in the problems in which the discontinuities of stresses have no physical interpretations. Among the authors who contribute to developing this theory, it has studied existence, structural stability, convergence and spatial behavior of this theory [22], it was introduced the generalized Fourier law to the field equations of the two-temperature theory of thermoelasticity and proved the uniqueness of the solution for homogeneous isotropic material [23], the propagation of harmonic plane waves studied [24]. Recently, authors have studied the uniqueness and growth solutions [25], for the model proposed [23]. The effect of three-phaselag on a two-temperature generalized thermoelasticity for the infinite medium with a spherical cavity had studied [26]. |
| The initial stress present in the medium also has a considerable effect on the propagation of waves (Biot, 1965). Initial stress in solids has the significant influence on the mechanical response of the material from an initially stressed configuration and has applications in geophysics, engineering structures, and in the behavior of soft biological tissues. Initial stress arises from processes, such as manufacturing or growth and is present in the absence of applied loads. It has studied the effect of hydrostatic initial stress and rotation with Green-Naghdi (type III) thermoelastic half space with two-temperature [27]. It has studied the effect of initial stress on a generalized thermoelastic medium with the three-phase-lag model under temperature-dependent properties [28]. Effect of rotation and initial stress on an infinite generalized magneto-thermoelastic diffusing body with a spherical cavity had investigated [29]. Hall effects on unsteady flow due to no coaxial rotating disk and a fluid at infinity were studied [30]. Flow induced by noncoaxial rotation of a porous disk executing non-torsion oscillating and second grade fluid rotating at infinity was discussed [31]. |
| The present paper is concerned with the investigations related to the effect of rotation and initial stress with twotemperature on a generalized thermoelastic medium based on the three-phase-lag model by applying the normal mode analysis. Also, the effects of rotation and initial stress on the physical quantities are discussed numerically and illustrated graphically. |
 |
FORMULATION OF THE PROBLEM
|
| We consider a homogeneous thermoelastic half-space with two-temperature rotating uniformly with angular velocity Ω = Ω n, where n is a unit vector representing the direction of the axis of rotation. All quantities are considered are functions of the time variable t and of the coordinates x and y. The displacement equation in the rotating frame has two additional terms [Schoenberg and Censor (1973)]: Centripetal acceleration Ω × (Ω × u ) due to time varying motion only and Coriolis acceleration 2Ω × u where ( 0) 1 2 u = u , u , is the dynamic displacement vector and angular velocity is Ω = (0, 0, Ω ) . These terms, do not appear in non-rotating media. |
BASIC EQUATIONS
|
| The field equations and constitutive relations for a homogeneous isotropic thermoelastic solid with hydrostatic initial stress and rotation in the absence of incremental body forces and heat source are given by three phase lag model, |
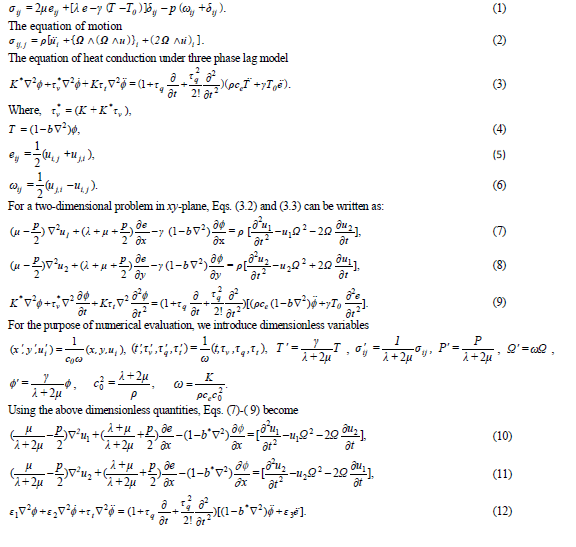 |
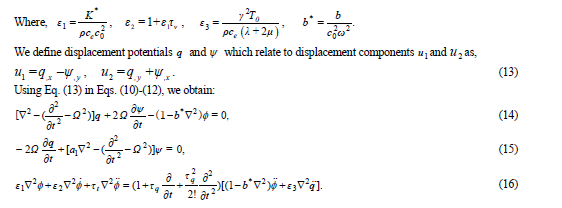 |
NORMAL MODE ANALYSIS
|
 |
 |
THE BOUNDARY CONDITIONS
|
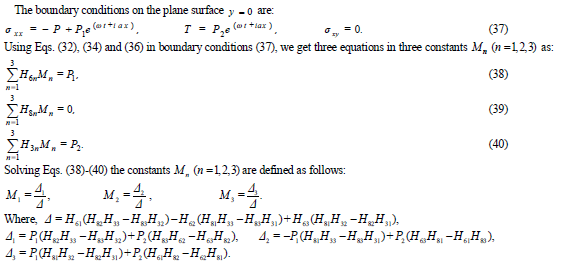 |
NUMERICAL RESULTS
|
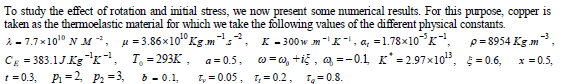 |
| The numerical technique, outlined above, was used for the distribution of the real part of the temperature T , the displacement components u ,v and the stress components , xx ïÃÂó , yy ïÃÂó xy ïÃÂó for the problem. Here, all the variables are taken in non-dimensional form the result. Fig. 1-6 show the distribution of the physical quantities based on L-S, G-N III and 3PHL in the case of p = 0,1 . Fig. 1 depicts that the displacement component u increases with the decrease of initial stress in the three theories. In the absence of initial stress (i.e. p = 0 ), u begins to increase then smooth decreases again to try to return to zero at infinity and in the presence of initial stress (i.e. p = 1), u decreases and increases until it develops to zero. |
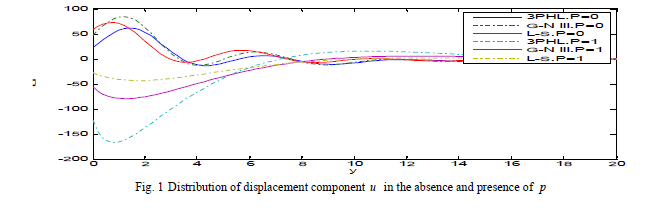 |
| Fig. 2 exhibits that the displacement component v decreases with the decrease of initial stress and it is increasing with the increase of initial stress, based on L-S, G-N III and 3PHL, that’s means that the displacement v is directly proportional to initial stress, and take the form of a wave until it develops to zero. Fig. 3 demonstrates that the behavior of temperature T decays meaning that the temperature decrease for p = 0,1 and take the form of a wave until it develops to zero. |
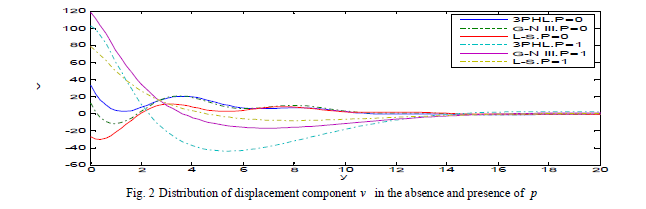 |
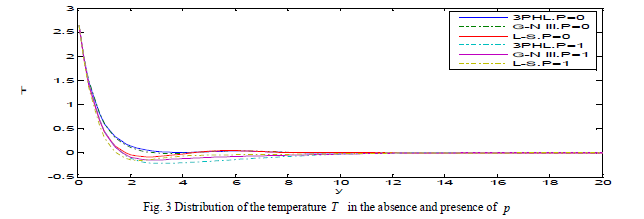 |
| Fig. 4 represents that the stress component xy ïÃÂó increase with the increase of initial stress p in three theories and take the form of the wave until it develops to zero, and decreasing with the decrease of the initial stress in three theories and take the form of the wave until it develops to zero. |
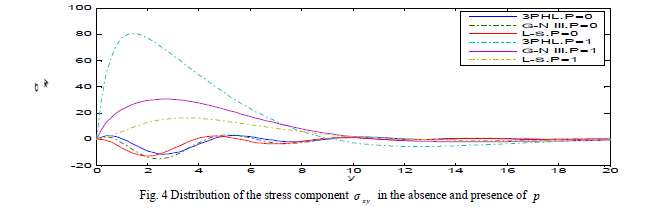 |
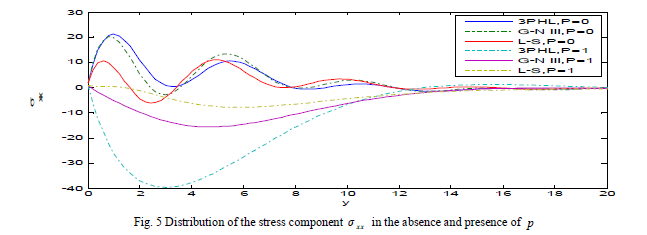
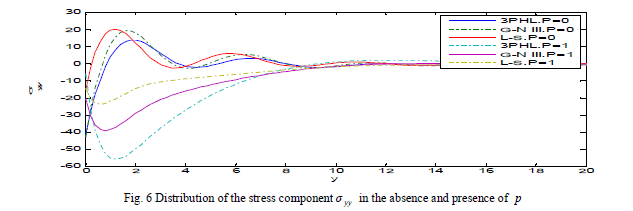
| Fig. 5 depicts that the stress component xx σ begins from the value 2 and satisfies the boundary condition at y ïÃâ¬Ã½ 0 in three theories. The stress component xx σ increase with the decrease of initial stress and decays to zero. Fig. 6 explains that the stress component yy ïÃÂó increase with the decrease of initial stress and take the form of the wave until it develops to zero. Figs. 7-12 exhibit the distribution of the physical quantities based on L-S, G-N III and 3PHL in the case of Ω = 0, 0.2. |
 |
 |
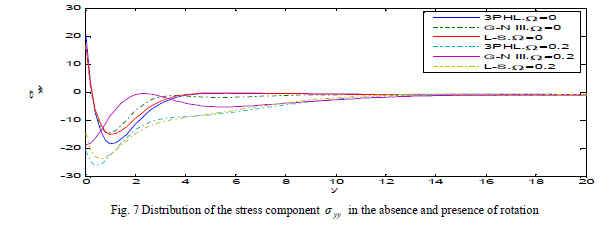
| Fig. 7 shows that at Ω = 0, the stress component yy ≤ is decreasing to a minimum value in the range 0 ≤ y ≤ 2, while, increases in the range 2 ≤ y ≤ 4 and decays to zero in L-S, G-N III and 3PHL theories, but at Ω = 0.2, it decreases to a minimum value in the range 0 ≤ y ≤ 1 , and increases in the range 1 ≤ y ≤ 3, until it develops to zero. |
 |
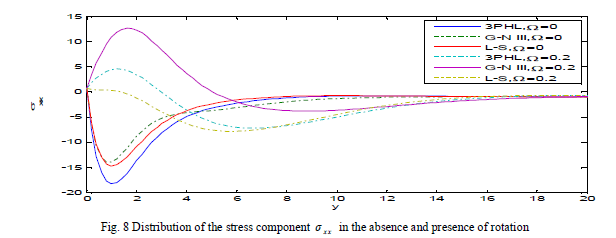
| Fig. 8 shows that at Ω = 0, the stress component xx σ satisfies the boundary condition and decreasing to a minimum value in the range 0 ≤ y ≤ 1, while, increases in the range 1 ≤ y ≤ 6 and decays to zero in the context of three theories. However, at Ω = 0.2, it increases in the range 0 ≤ y ≤ 2, then, decreases in the range 2 ≤ y ≤ 8 and decays to zero in the three theories. |
 |
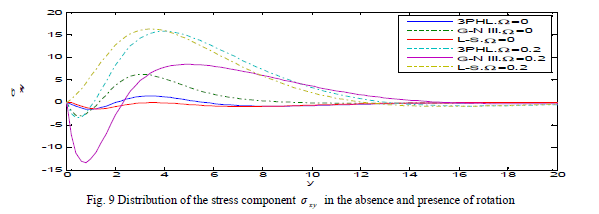
| Fig. 9 explains that in the absence of rotation the stress component σ xy decreases in the range 0 ≤ y ≤ 1, in three theories, and increases in the range 1≤ y ≤ 3. While in the presence of rotation, σ xy decreases in the range 0 ≤ y ≤ 1 , then, increases in the range 2 ≤ y ≤ 5 and take the form of the wave until it develops to zero in L-S and G-N III and 3PHL theories. |
 |
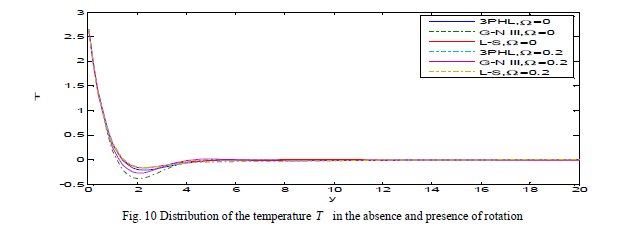 |
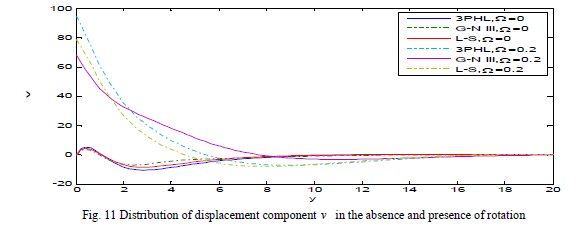
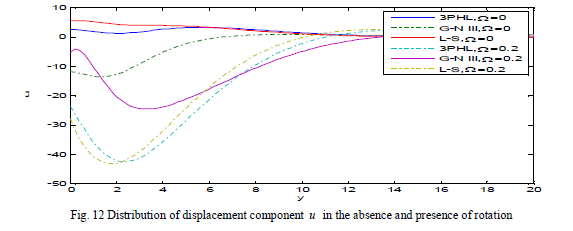
| Fig. 10 demonstrates that the temperature satisfies the boundary condition at y ≤ 0 and decreases, in the three theories at Ω = 0, 0.2, to a minimum value in the range 0 ≤ y ≤ 2 and increasing in the range 2 ≤ y ≤ 4, until it decays to zero. Fig. 11 shows that the displacement component v increases at Ω = 0.2, in three theories, and decreases at Ω = 0, that’s mean that the displacement component v increases with the increase of rotation and take the form of the wave until it develops to zero. Fig. 12 depicts that the displacement component u increases with the decrease of rotation and try to return to zero at infinity. |
 |
 |
CONCLUSION
|
| The figures obtained by comparing the three theories, important phenomena are observed: |
| 1. Analytical solutions based upon normal mode analysis of the thermoelastic problem in solids have been developed. |
| 2. The method that is used in the present article is applicable to a wide range of problems in hydrodynamics and thermoelasticity. |
| 3. There are significant differences in the field quantities under GN-III, 3PHL and L-S theories.. |
| 4. The presence of the initial stress and rotation plays a significant role in all physical quantities. |
| 5. All the physical quantities satisfy the boundary conditions. |
| 6. The comparison of different theories of thermoelasticity, i.e. L-S theory, the model of 3PL and the GN-III is carried out. |
| 7. The value of all the physical quantities converges to zero, and all the functions are continuous. |
References
|
- Hetnarski, R.B. and Ignaczak, J. ''Generalized Thermoelasticity", Journal of Thermal stresses, vol 22, pp. 451-476, 1999.
- Lord, H.W. and Shulman, Y. "A generalized dynamical theory of thermoelasticity", Journal of the Mechanics and Physics of Solids, vol. 15,pp. 299-309, 1967.
- Green, A.E. and Lindsay K.A.''Thermoelasticity", Journal of Elasticity, vol. 2, pp. 1-7, 1972.
- Hetnarski, R.B. and Ignaczak, J. "Soliton-like waves in a low temperature non-linear thermoelastic solid", International journal of EngineeringScience, vol. 34, pp. 1767-1787, 1996.
- Sharma, J.N. and Sidhu, R.S. "On the Propagation of Plane harmonic waves in anisotropic generalized thermoelasticity", International Journalof Engineering Science, vol. 24, pp. 1511-1516, 1986.
- Singh, H. and Sharma, J.N."Generalizedthermoelastic waves in transversely isotropic media", Journal of the Acoustical Society of America,vol. 85, pp. 1407-1413, 1985.
- Singh, H. and Sharma, J.N. "Generalized thermoelastic waves in anisotropic media", Journal of the Acoustical Society of America, vol. 77, pp.1046-1053, 1985.
- Tzou, D.Y. "Aunified field approach for heat conduction from macro to micro scales", Asme journal of heat transfer, vol. 117, pp. 8-16, 1995.
- Chandrasekharaiah, D.S. "Hyperbolic thermoelasticity: A review of recent Literature", Applied Mechanics Reviews, vol. 51, pp. 705-729,1998.
- Roy Choudhuri, S. K. "On thermoelastic three phase lag model", Journal of Thermal Stresses, vol. 30, pp. 231-238, 2007.
- Quintanilla, R. and Racke, R. "A note on stability in three-phase-lag heat Conduction", International Journal of Heat and Mass Transfer, vol.51, pp. 24-29, 2008.
- Kar, A. and Kanoria, M. "Generalized thermoelastic functionally graded orthotropic hollow sphere under thermal shock with three-phase-lageffect", European Journal of Mechanics - A/Solids, vol. 28, pp. 757-767, 2009.
- Schoenberg, M. and Censor D. "Elastic waves in rotating media", Quarterly Journal of Mechanics and Applied Mathematics, vol. 31, pp. 115-125, 1973.
- Chand, D. Sharma, J. N. and Sud, S. P. "Transient generalized magneto-thermoelastic waves in a rotating half space", International Journal ofEngineering Science, vol. 28, pp. 547-556, 1990.
- Clarke, N. S. and Burdness, J. J. "Rayleigh waves on rotating surface", ASME Journal of Applied Mechanics. vol. 61, pp. 724-726, 1994.
- [Destrade, M. "Surface waves in rotating rhombic crystal", Proceeding of the royal society of London. Series A, vol. 460, pp. 653-665, 2004.
- Othman, M. I. A. and Song, Y. Q. "The effect of rotation on 2-D thermal shock problems for a generalized magneto-thermoelasticity halfspace under three theories", Mult. Model Math. & Structure, vol. 5, pp. 43-58, 2009.
- Gurtin, M.E. and Williams, W.O. "An axiom foundation for continuum Thermodynamics", Archive for Rational Mechanics and Analysis, vol.26, pp. 83-117, 1967.
- Chen, P.J. and Gurtin, M.E. "On a theory of heat conduction involving two temperatures", ZeitschriftfürangewandteMathematik und Physik,vol. 19, pp. 614-627, 1968.
- Chen, P.J. and Gurtin, M.E. "A note on non-simple heat Conduction, Z. ZeitschriftfürangewandteMathematik und Physik, vol. 19, pp. 969-970, 1968.
- IeÃâ¦ÃŸan, D. "On the linear coupled thermoelasticity with two temperatures", ZeitschriftfürangewandteMathematik und Physik, vol, 21, pp. 583-591, 1970.
- Quintanilla, R. "On existence, structural stability, convergence and spatial behavior in thermoelasticity with two temperatures", ActaMechanica, vol. 168, pp. 61–73, 2004.
- Youssef, H. M. "Theory of two-temperature generalized thermoelasticity", IMA journal of applied mathematics, vol. 71, pp. 383-390, 2006.
- Puri, P. and Jordan, P. "On the propagation of harmonic plane waves under the two-temperature theory", International Journal of EngineeringScience, vol. 44, pp. 1113-1126, 2006.
- Magaña, A. and Quintanilla, R. "Uniqueness and growth of solutions in two-temperature generalized thermoelastic theories", Mathematics andMechanics of Solids, vol. 14, pp. 622-634, 2009.
- Banik, S. and Kanoria, M. "Effects of three-phase-lag on two-temperature generalized thermoelasticity for infinite medium with sphericalcavity", Journal of Applied Mathematics and Mechanics, vol. 33, pp. 483-498, 2011.
- Ailawalia, P. and Budhiraja, S. "On studied effect of hydrostatic initial stress and rotation in Green-naghdi (type III) thermoelastic half spacewith two temperature, International Journal of Applied Mathematics and Mechanics, vol. 7, pp. 93-110, 2011.
- Othman, M. I. A ,Hasona, W. M. and Eraki, E. E. M. "The effect of initial stress on generalized thermoelastic medium with three-phase-lagmodel under temperature-dependent properties" , Canadian Journal of physics, vol. 92, pp. 448-457, 2014.
- Abd-Alla, A.M. and Abo-Dahab, S.M. "effect of rotation and initial stress on an infinite generalized magneto-thermoelastic diffusion bodywith a spherical cavity", Journal of Thermal Stresses, vol. 35, pp. 892-912, 2012.
- Hayat, T. Ellahi, R. and Asghar, S. "Hall effects on unsteady flow due to non-coaxially rotating disk and a fluid at infinity", ChemicalEngineering Communications, vol. 195, pp. 958-976, 2008.
- Hayat, T. Ellahi, R. Asghar, S. and Siddiqui, AM "Flow induced by non-coaxial rotation of a porous disk executing non-torsional oscillatingand second grade fluid rotating at infinity", Applied Mathematical Modelling, vol. 28, pp. 591-605, 2004.
|