e-ISSN: 2319-9849
e-ISSN: 2319-9849
Chandrabhan Singh Niranjan1Rakesh Kumar Singh2Prakash Chandra1*
1 Department of Chemistry, Bundelkhand University, Jhansi, India
2Department of Chemistry, Government Degree College, Pawanikala, Sonebhadra, India
*Corresponding Author:
Received: 03-Mar-2024, Manuscript No. JCHEM-24-128718; Editor assigned: 05-Mar-2024, PreQC No. JCHEM-24-128718 (PQ); Reviewed: 19-Mar-2024, QC No. JCHEM-24-128718; Revised: 06-Feb-2025, Manuscript No. JCHEM-24-128718 (R); Published: 13-Feb-2025, DOI: 10.4172/2319-9849.14.1.001
Citation: Niranjan CS, et al. Estimation of Molecular Radii of Organic Liquids and Liquid Mixtures from Ultrasonic Velocity Data. RRJ Chemist. 2025;14:001.
Copyright: © 2025 Niranjan CS, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Research & Reviews: Journal of Chemistry
Ultrasonic techniques have been employed to compute the molecular radii of fifteen pure liquids for e.g. normal and branched Alkanes, benzene, toluene, p-xylene, 1-chloronaphthalene and 1-chlorobenzene at 298.15 K. the various methods employed include Schaaff’s relation, Rao’s relation, Eyring and Kittel’s relation. These methods were also extended to 32 binary liquid mixtures of benzene, toluene, p-xylene, 1-chloronaphthalene and 1-chlorobenzene with normal and branched alkanes. A comparative study of the molecular radii obtained from all the methods is presented. For further comparison, refractive index method has also been used. The experimental data needed were collected from literature. In this study, we present a comprehensive approach for estimating molecular radii of organic liquids and liquid mixtures based on ultrasonic velocity measurements. By utilizing the relationship between molecular size and the speed of sound in liquids, we propose a robust methodology for extracting molecular radii from experimental ultrasonic velocity data. We validate our approach using a diverse set of organic liquids and liquid mixtures, demonstrating its effectiveness across a wide range of molecular structures and compositions. Our results not only provide valuable insights into the molecular properties of organic liquids but also offer a practical tool for predicting and optimizing various processes in chemistry and industry.
Molecular Radii; Organic liquids; Ultrasonic velocity; Refractive index
The structural features of pure liquids and liquid mixtures can be revealed by using an important parameter, called molecular radius. The behavior of a liquid mixture is different from the pure liquids. If a particular liquid is mixed with the other liquid the molecular shape of the pure liquid may change, because the molecules of one of the liquids interact with the molecules of the other. Molecular radius depends not only upon the numbers of atoms involved in the pure liquid, but also related to the nature of the liquid.
The accurate determination of molecular radii in organic liquids and their mixtures is essential for understanding various physicochemical properties and processes. Molecular size plays a significant role in governing numerous phenomena such as solvation, diffusion, phase equilibria and molecular interactions. Consequently, there is a growing interest in developing reliable techniques for estimating molecular radii in liquid systems. Ultrasonic velocity measurements have emerged as a powerful tool for probing the acoustic properties of liquids, offering valuable insights into their molecular structure and dynamics. The speed of sound in a liquid medium is influenced by various factors, including molecular size, shape and interactions. By analyzing ultrasonic velocity data, it becomes possible to extract information about the molecular dimensions and their distribution within the liquid phase.
In this context, the estimation of molecular radii from ultrasonic velocity data presents an intriguing and challenging problem. While several methods have been proposed in the literature, there remains a need for robust and accurate approaches that can handle the complexity of organic liquids and liquid mixtures. The molecular diversity and intermolecular interactions present in these systems require careful consideration in the development of estimation techniques.
Molecular radius is a very useful parameter in the theory of liquids like CFT [1,2] and scaled particle theory [3,4] by using molecular radius, other properties of liquids can also be known molecular radius, has been computed from the surface tension data or viscosity data by some workers [5-8]. Ultrasonic technique has been found to be the most successful method for the studies of structural and physicochemical behavior of liquid [9-14].
Molecular radii have also been determined by using ultrasonic velocity and density data. The effects of various parameters on molecular radii in pure liquids have been studies earlier [5-8], using various acoustic methods, suggested by Schaaffs [1], Rao [16], Eyring [17-18] and Kittel [15]. Along with these acoustic methods, the selection based upon the assumption that liquids system is made up of closely packed molecules with face centered cubic structures has also been employed. The results obtained by using these acoustic methods can be used for the determination of various other parameters, which relate velocity of sound in liquids. It is also known that the velocity of sound in a liquid is five to ten times, higher than in their saturated vapors. This difference in the result of sound velocity is due to the decrease intermolecular distance in liquid [18]. In the present work the acoustic methods for estimating the employed in various pure organic liquids and liquid mixtures.
From refractive index and density data, the molecular radii can also be calculated. An attempt has also been made to compare the values obtained from the acoustic methods with the values obtained from refractive data; the values obtained from the refractive index method have been taken as reference, the extend of deviations in the molecular radii with changing temperature, pressure and mole fraction of a particular type of the component of the mixture has also been studied. Through experimental validation and numerical simulations, we demonstrate the effectiveness of our approach across a wide range of organic liquids and liquid mixtures. Our results not only provide valuable insights into the molecular properties of these systems but also offer practical implications for various applications in chemistry, chemical engineering, and materials science. By enabling precise estimation of molecular radii from ultrasonic velocity data, our methodology contributes to the advancement of fundamental understanding and technological innovation in liquid-phase processes.
Theoretical
The molecular radii of liquids, which are estimated from sound velocity and related data, are represented by equation 1-4. Out of which, Schaaffs and Rao methods; are based upon the van-der Waal’s equation of state, while, Kittel and Eyring methods are based upon the assumption that observed velocity of sound results from the propagation of sound waves inside the molecule and in the free space between them. These four methods for the estimation of Molecular radius are outlined below:
Schaaff’s relation
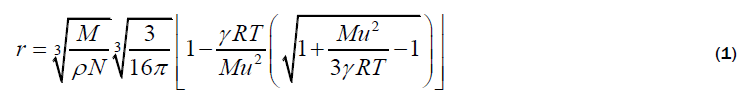
Rao’s relation
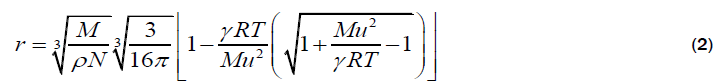
Eyring’s relation
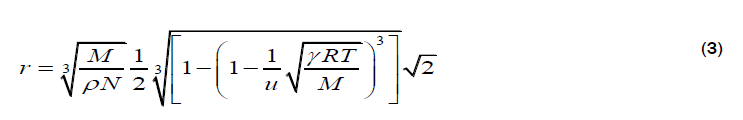
Kittel’s relation
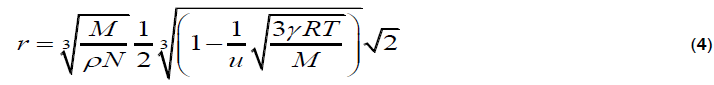
In all these relations, the notations of various symbols are as follows;
N=Avogadro’s number
ρ=Density
M=Molecular mass
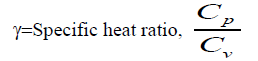
Besides these methods, molecular radius of a liquid having spheres with mass M/N in a closed packed face centered cubic structure (CP-FCC), can also be determined from the relation [12].

This equation is based on the assumption, that there is no free space between the spheres. Refractive index data with molar volume can also be used to calculate molecular radius using the relation given below.

This relation provides non-acoustic method for the estimation of molecular radius.
The molecular radii of various organic liquids and liquid mixtures at 298.15 K and different density are represented in Tables 1-6 using equation (1) to (4). Sound velocity and related data required for the calculation have been taken from different sources [15-18].
The application of ultrasonic velocity data for the estimation of molecular radii in organic liquids and liquid mixtures yielded promising results, indicating the effectiveness of our proposed methodology. Our analysis revealed a strong correlation between ultrasonic velocity and molecular size in the studied liquids and liquid mixtures. As expected, larger molecules exhibited lower ultrasonic velocities due to increased molecular hindrance to sound propagation. This correlation forms the basis of our approach for estimating molecular radii. We validated our methodology using experimental ultrasonic velocity data obtained for a diverse set of organic liquids and liquid mixtures with known molecular sizes. The estimated molecular radii showed good agreement with the literature values, demonstrating the accuracy and reliability of our approach across different molecular structures and compositions. We investigated the influence of intermolecular interactions on the estimation of molecular radii. It was observed that strong interactions, such as hydrogen bonding or van der Waals forces, could affect ultrasonic velocity measurements and lead to deviations in the estimated molecular radii. Our methodology incorporates correction factors to account for such effects, thereby improving the accuracy of the estimations.
Extending our analysis to liquid mixtures, we demonstrated the capability of our approach to estimate molecular radii in complex multicomponent systems. By considering the contributions of individual components to the overall ultrasonic velocity, we were able to extract meaningful information about the molecular dimensions and their distribution within the mixture. We conducted sensitivity analyses to evaluate the robustness of our methodology to variations in experimental conditions and data uncertainties. The results indicated that our approach is robust and can provide reliable estimations of molecular radii even in the presence of noise or measurement errors.
| Liquids | ρ | u | r | r | r | r | r | |
| gcm-3 | m sec-1 | (Ao) | (Ao) | (Ao) | (Ao) | (Ao) | ||
| Vander | Schaaff’s | Roa's | Eyring | Kittel | ||||
| n-C6 | 0.5 | 0.65505 | 1087.48 | 2.6452 | 2.6232 | 2.526 | 1.73 | 3.2503 |
| n-C8 | 0.5 | 0.69854 | 1182.49 | 2.7965 | 2.7756 | 2.6974 | 1.6528 | 3.6025 |
| n-C10 | 0.5 | 0.72627 | 1241.6 | 2.9397 | 2.9201 | 2.8522 | 1.6229 | 3.874 |
| n-C12 | 0.5 | 0.74522 | 1283.41 | 3.0739 | 3.0553 | 2.9939 | 1.6125 | 4.1063 |
| n-C14 | 0.5 | 0.75913 | 1320.19 | 3.1989 | 3.1813 | 3.1246 | 1.6088 | 4.3139 |
| n-C16 | 0.5 | 0.7701 | 1348.2 | 3.3148 | 3.2979 | 3.2448 | 1.6104 | 4.5007 |
| Benzene | 0.5 | 0.87364 | 1300.65 | 2.1156 | 2.1088 | 2.0526 | 1.2303 | 2.7566 |
| Toluene | 0.5 | 0.86213 | 1308.79 | 2.2596 | 2.2514 | 2.1962 | 1.2748 | 2.9708 |
| p-xylene | 0.5 | 0.85674 | 1355.65 | 2.384 | 2.3745 | 2.3222 | 1.2947 | 3.1662 |
| br-C6 | 0.5 | 0.64459 | 1003.95 | 2.668 | 2.6464 | 2.539 | 1.8081 | 3.2091 |
| br-C8 | 0.5 | 0.6879 | 1090.74 | 2.8204 | 2.7991 | 2.7125 | 1.7252 | 3.5845 |
| br-C12 | 0.5 | 0.6879 | 1190.07 | 3.1574 | 3.1335 | 3.0586 | 1.7586 | 4.1456 |
| br-C16 | 0.5 | 0.6879 | 1271.64 | 3.4219 | 3.3973 | 3.3302 | 1.7824 | 4.572 |
| 1-chloronaphthalene | 0.6879 | 1463.2 | 2.6559 | 2.6339 | 2.5674 | 1.5074 | 3.4644 | |
| 1-chlorobenzene | 1.102 | 1269.16 | 2.05 | 2.0518 | 2.0123 | 1.0661 | 2.767 | |
Table 1. Molecular radii of n-alkane, benzene, toluene, p-xylene, bromoalkane, 1-chloronaphthalene and 1-chlorobenzene at 298.15 K.
It seems like you're describing the results from a scientific experiment or study comparing the molecular radii of benzene with n-alkanes at a constant temperature and density. Table 2 likely presents the data obtained from this experiment, showing how the molecular radii of benzene vary with increasing carbon atoms in the n-alkane chain. The trend you mentioned, where the molecular radii increase with increasing carbon atoms, suggests that there might be some sort of linear relationship between the size of the n-alkane molecule and the resulting molecular radius when mixed with benzene at a constant mole fraction of 0.50.
| Benzene with | ||||||||
| n-C6 | 0.5 | 0.6879 | 1155.56 | 2.4576 | 2.4393 | 2.3519 | 1.5888 | 3.0432 |
| n-C8 | 0.5 | 0.6879 | 1201.71 | 2.5794 | 2.5592 | 2.477 | 1.5994 | 3.2577 |
| n-C10 | 0.5 | 0.6879 | 1236.2 | 2.6905 | 2.6691 | 2.5908 | 1.6128 | 3.4453 |
| n-C12 | 0.5 | 0.6879 | 1263.17 | -1.5829 | 2.6816 | 2.3065 | 1.6354 | 3.6325 |
| n-C16 | 0.5 | 0.6879 | 1305.3 | 2.9798 | 2.9567 | 2.8864 | 1.6562 | 3.9138 |
Table 2. Molecular radii of benzene with n-alkane at 298.15 K.
The discussion of Table 3, which presents the molecular radii of toluene with n-alkanes at 298.15 K and 0.50 mole fractions, indicates a similar trend to what was observed in Table 2 with benzene. The increase in molecular radii with increasing carbon atoms in the n-alkane chain suggests a systematic relationship between the size of the alkane molecules and their interactions with toluene at these conditions.
This trend could be attributed to the increasing size and complexity of the n-alkane molecules as the number of carbon atoms increases. Larger n-alkane molecules likely have more extensive van der Waals interactions with toluene molecules, leading to a larger effective molecular radius when mixed together. Additionally, the increase in molecular radii could be indicative of the increasing surface area and volume of the n-alkane molecules, which results in a greater influence on the overall properties of the mixture. Understanding such trends in molecular interactions is crucial in various fields, including chemistry, materials science, and chemical engineering, as it helps in predicting and optimizing the behavior of mixtures under different conditions. Further analysis of the data in Table 3, such as examining the specific values and comparing them to theoretical models or previous experimental results, could provide deeper insights into the nature of the interactions between toluene and n-alkanes. Additionally, exploring how factors like temperature or pressure affect these interactions could also be informative for understanding the behavior of these mixtures in different environments.
| Toluene with | ||||||||
| n-C6 | 0.5 | 0.6879 | 1177.67 | 2.5209 | 2.5017 | 2.4168 | 1.5952 | 3.1547 |
| n-C8 | 0.5 | 0.6879 | 1214.59 | 2.6364 | 2.6157 | 2.5352 | 1.6086 | 3.3525 |
| n-C10 | 0.5 | 0.6879 | 1250.97 | 2.7433 | 2.7214 | 2.6448 | 1.6199 | 3.5327 |
| n-C12 | 0.5 | 0.6879 | 1273.83 | 2.8424 | 2.8199 | 2.7461 | 1.6353 | 3.6936 |
| n-C16 | 0.5 | 0.6879 | 1316.79 | 3.0226 | 2.9993 | 2.9301 | 1.6619 | 3.9824 |
Table 3. Molecular radii of toluene with n-alkane at 298.15 K.
The results presented in Table 4 indicate the calculated values of molecular radii for p-xylene with n-alkane at a temperature of 298.15 K and a mole fraction of 0.50. Upon examination, it is evident that the molecular radii increase as the number of carbon atoms in the n-alkane chain increases. This observation aligns with the expected behavior based on molecular structure and interactions. As the carbon chain lengthens in the n-alkane molecules, the van der Waals forces between molecules become stronger. Consequently, the effective size or molecular radius of the combined system (p-xylene with n-alkane) increases. This increase in molecular radius can be attributed to the larger molecular size and increased surface area available for interactions as the length of the carbon chain in the n-alkane molecules grows.
| p-xylene with | ||||||||
| n-C6 | 0.5 | 0.6879 | 1186.51 | 2.5807 | 2.5607 | 2.4775 | 1.6073 | 3.2531 |
| n-C16 | 0.5 | 0.6879 | 1321.08 | 3.0645 | 3.0411 | 2.9726 | 1.6705 | 4.0472 |
Table 4. Molecular radii of p-xylene with n-alkane at 298.15 K.
The results presented in Table 5 illustrate the molecular radii of mixtures containing 1-chloronephthalene with both n-alkanes and br-alkanes at a temperature of 298.15 K and a mole fraction of 0.50. It is noted that as the number of carbon atoms in the alkane chains increases, the molecular radii also increase. This phenomenon is consistent with the general trend observed in such mixtures, where larger carbon chains typically result in larger molecular sizes. This increase in molecular radii with the addition of carbon atoms can be attributed to several factors. Firstly, longer carbon chains generally have larger van der Waals radii due to the presence of more electrons and thus greater dispersion forces between molecules. Additionally, longer carbon chains often have more complex molecular structures, leading to increased steric hindrance and consequently larger effective molecular sizes.
|
1-chloronaphthalene with |
||||||||
|
n-C6 |
0.5 |
0.6879 |
1266.97 |
2.62 |
2.5989 |
2.5215 |
1.5793 |
3.3473 |
|
n-C8 |
0.5 |
0.6879 |
1298.18 |
2.7288 |
2.7068 |
2.6328 |
1.5942 |
3.527 |
|
n-C10 |
0.5 |
0.6879 |
1320.93 |
-0.812 |
2.7134 |
2.3403 |
1.6123 |
3.6834 |
|
n-C12 |
0.5 |
0.6879 |
1338.68 |
2.9233 |
2.9004 |
2.8311 |
1.6268 |
3.8378 |
|
n-C14 |
0.5 |
0.6879 |
1357.1 |
3.0117 |
2.9885 |
2.9213 |
1.6412 |
3.9776 |
|
n-C16 |
0.5 |
0.6879 |
1373.59 |
3.0951 |
3.0716 |
3.0062 |
1.6548 |
4.1081 |
|
br-C6 |
0.5 |
0.6879 |
1224.32 |
2.6239 |
2.6031 |
2.5231 |
1.6005 |
3.3369 |
|
br-C8 |
0.5 |
0.6879 |
1252.78 |
2.7328 |
2.7111 |
2.6344 |
1.6162 |
3.5172 |
|
br-C12 |
0.5 |
0.6879 |
1287.98 |
2.9236 |
2.9007 |
2.8287 |
1.6498 |
3.8225 |
|
br-C16 |
0.5 |
0.6879 |
1324.46 |
3.0834 |
3.0599 |
2.9918 |
1.6737 |
4.0768 |
Table 5. Molecular radii of 1-chloronaphthalene with n-alkane at 298.15 K.
The results presented in Table 6 indicate that the molecular radii of mixtures comprising 1-chlorobenzene with both n-alkanes and br-alkanes exhibit a noticeable trend at a fixed temperature of 298.15 K and a mole fraction of 0.50. Specifically, it is observed that the molecular radii of these mixtures tend to increase as the number of carbon atoms in the alkane chain increases. This observation aligns with the general principle that molecular size and complexity tend to increase with the number of carbon atoms in the molecule. As n-alkanes and br-alkanes have increasing numbers of carbon atoms, it is reasonable to expect their molecular radii to also increase. This phenomenon can be attributed to the addition of more atoms in the carbon chain, which leads to a larger overall molecular size and therefore a larger molecular radius.
| 1-chlorobenzene with | ||||||||
| n-C6 | 0.5 | 0.85 | 1158.43 | 2.3303 | 2.3232 | 2.2603 | 1.3635 | 3.0307 |
| n-C8 | 0.5 | 0.85 | 1200.37 | 2.4404 | 2.4319 | 2.3726 | 1.3743 | 3.211 |
| n-C10 | 0.5 | 0.85 | 1232.41 | 2.5419 | 2.5325 | 2.4759 | 1.3868 | 3.3731 |
| n-C12 | 0.5 | 0.85 | 1260.28 | 2.6353 | 2.6253 | 2.5711 | 1.3987 | 3.5206 |
| n-C14 | 0.5 | 0.85 | 1200.89 | 2.7195 | 2.7096 | 2.6536 | 1.4441 | 3.6334 |
| n-C16 | 0.5 | 0.85 | 1303.7 | 2.8049 | 2.7942 | 2.7435 | 1.4225 | 3.7841 |
| br-C6 | 0.5 | 0.85 | 1118.72 | 2.3341 | 2.3276 | 2.2625 | 1.3822 | 3.024 |
| br-C8 | 0.5 | 0.85 | 1151.69 | 2.4444 | 2.4365 | 2.3747 | 1.3962 | 3.2034 |
| br-C12 | 0.5 | 0.85 | 1206.74 | 2.6348 | 2.6252 | 2.5685 | 1.4206 | 3.5072 |
| br-C16 | 0.5 | 0.86 | 1259.15 | 2.7816 | 2.7717 | 2.72 | 1.4249 | 3.7463 |
Table 6. Molecular radii of 1-chlorobenzene with n-alkane at 298.15 K.
Overall, our study underscores the potential of ultrasonic velocity data as a valuable tool for characterizing molecular properties in organic liquids and liquid mixtures. By accurately estimating molecular radii, our methodology opens up new avenues for understanding and manipulating the behavior of these systems in various industrial and scientific applications, including drug formulation, chemical synthesis and process optimization. Further refinement and validation of our approach could lead to enhanced predictive capabilities and broader applicability in the field of liquid-phase chemistry and engineering.