ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Hasan Abdulhadi Ajel1 and Abdulnasser M. Abbas2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The structural behaviour of concrete - filled steel tube (CFST) columns has been investigated using experimental and analytical studies. The effect of concrete compressive strength, thickness of steel tube, stiffeners and longitudinal reinforcement were considered. Specimens that have been studied consist of sixteen square samples with dimensions of 150 mm ×150 mm × 300 mm height, and fifteen circular samples of 150 mm diameter and height of 300 mm. The tested samples were studied analytically using three dimensional finite element representation by ANSYS (ver. 12.1) computer program. Eight nodes brick elements SOLID 65 and SOLID 45 were used to simulate concrete and steel tube respectively. While two nodes element LINK 8 are used for steel rebar. The results obtained from finite element solution shows that, the convergence between analytical and experimental failure load varied from 2 to 15 %. While the effect of compressive strength of concrete on columns having width/thickness (b/t) or diameter/thickness (d/t) 37.5 is greater than columns which have (b/t) or (d/t) 50. Deformations of columns filled with normal concrete (25 MPa) are larger than those of columns filled with high strength concrete (60MPa). The effect of width-thickness (b/t) and diameter/thickness (d/t) ratio on the ultimate strength of (CFST) columns will have a reverse action, when of (b/t) or (d/t) decreases the caused increasing in ultimate load capacity of columns which is varied from 4.47 to13.37 % for square samples varied from 8.00 to 12.14% for circular samples depending on the type of stiffened, compressive strength of concrete and ratio of (b/t) and (d/t).
Keywords |
| Stub column, Composite column, Concrete-filled steel tube column. |
INTRODUCTION |
| Steel-concrete composite columns were used for over a century. At the beginning it was used to provide fire protection to steel structures. Afterwards, the concrete encased columns strength properties were also considered in the design. However, the researches into concrete filled steel tubes (CFST) did not begin until the 1960[1]. Nowadays, the composite structural elements are increasingly used in tall buildings, bridges and other types of structures. The steelconcrete composites are considered as an advantageous system for carrying large axial load benefitting from the interaction between the concrete and the steel section. The steel section reinforces the concrete to resist any bending moments, tensile and shear forces. The concrete in a composite column reduces the potential for buckling of the steel section in addition to resisting compressive loading. There are two types of steel-concrete composite columns which are commonly used in buildings. Those with steel section in-filled with concrete and those with steel section encased with concrete as shown in figure (1) [2]. |
| At a certain strain, the expansion of the concrete infill laterally increases until it reaches the lateral expansion of the steel. Keep in mind that the structural steel expansion remains constant in this stage and micro-cracking in the concrete begins to take place. This acceleration in the concrete expansion results in an interactive contact between the two materials. Hence, bond stresses are developed and the concrete will be subjected to tri-axial stresses while the structural steel to biaxial stresses [3]. |
| Longitudinal stress in the confining tube varies based on the transfer of force between the concrete and steel. The strain level at which confinement occurs is debated among researchers to range from 0.001 to 0.002. Some scientists such as Knowles and Park concluded that concrete confinement happens suddenly at a about (strain of 0.002) just as the concrete starts dilation [4]. While other researchers as Tsuji, et al. and Zhang, et al. proposed a steady increase in the concrete confinement starting right after the occurrence of micro-cracking in the concrete (strain of 0.001), till full confinement is met at a strain around 0.002 [5],[6] . In the second stage of loading where the confinement of the steel tube on the concrete is present, circumferential stresses are developed in the structural steel due to two factors: 1. Longitudinal stresses from loading. 2. Lateral pressure from concrete dilation. Based on the steel utilized in the composite element, the steel could have reached its capacity prior to their yield in this stage. If tube yielding occurs before this biaxial state of stress, the tube would not be able to sustain the normal yield stress, resulting in a transfer of load from tube to the concrete core. Conversely, if the confining tube has not yet yielded, the extra axial capacity needed from the steel tube before yielding will be reduced [7] . |
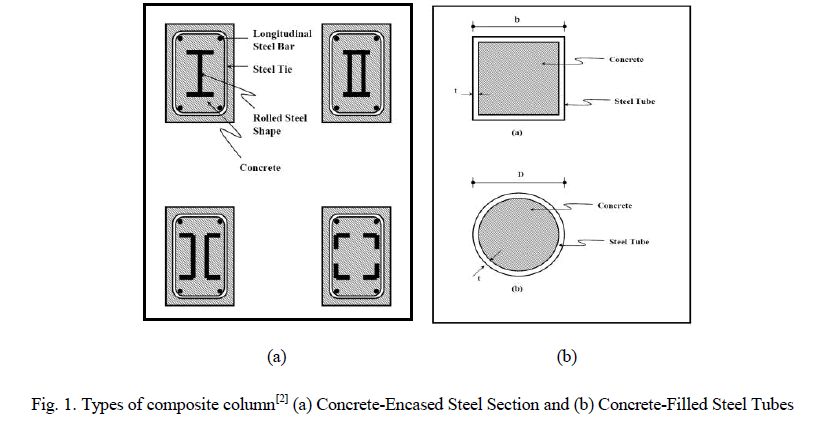 |
MATERIALS AND METHODS |
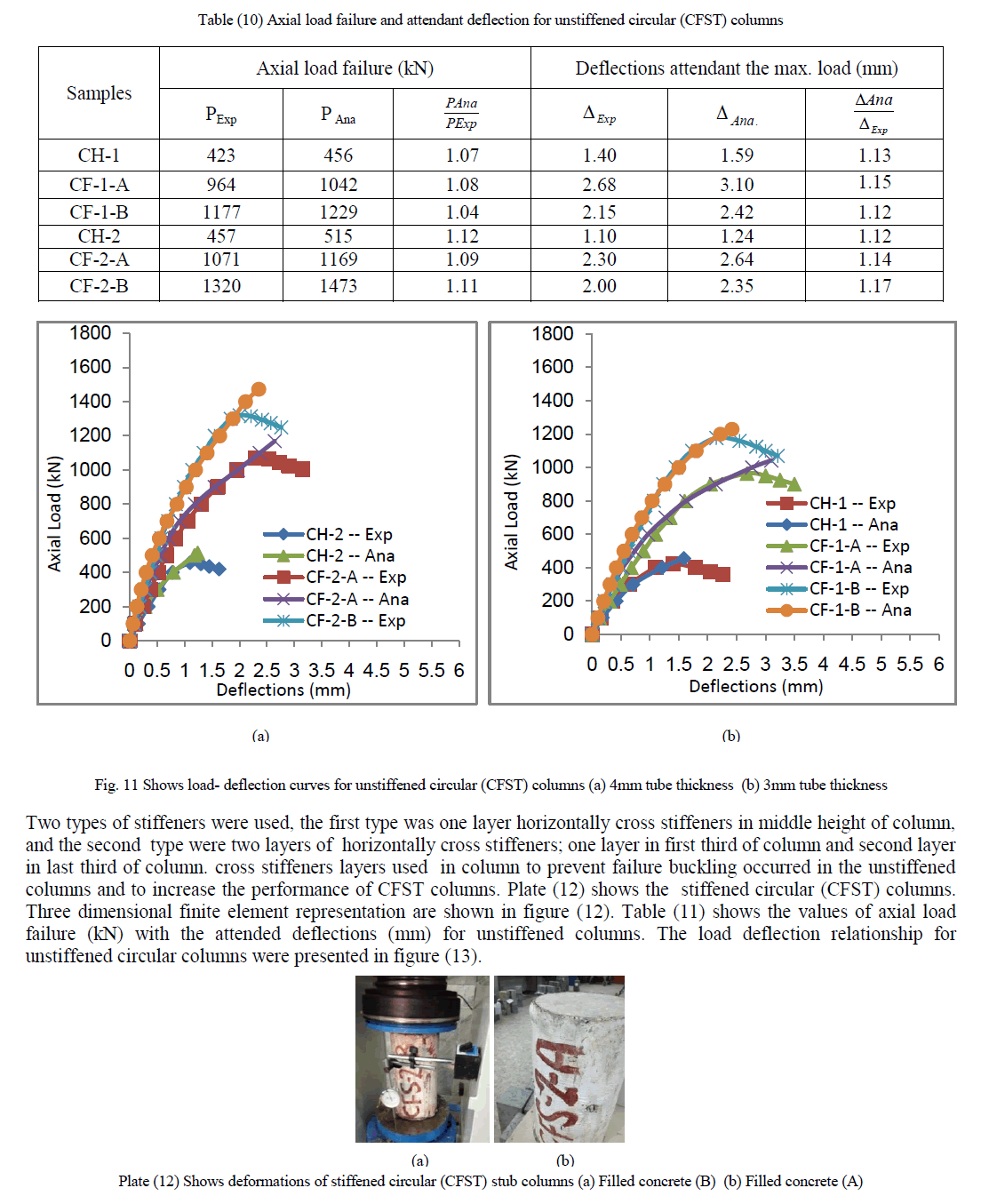
| The primary aim of this experimental work is to study the structural behaviour of concrete-filled steel tube stub columns. The experimental work included testing of sixteen square stub columns and fifteen circular stub columns subjected to concentric axial compression. The structural behaviour of the concrete-filled steel tube stub columns, depends on many parameters, including the properties of cement, sand, gravel, super plasticizer (glenium 51), steel plate and steel rebar. Standard tests according to the Iraqi specifications and American Society for Testing and Materials (ASTM) were conducted to determine the properties of materials. The types of concrete-filled steel tube stub columns specimens were taken in this study consists of filled concrete without stiffened, filled concrete with stiffened and filled concrete with reinforcement. Types of the used concrete are normal and high strength concrete. Plate (1), plate (2) and plate (3) shows unstiffened, stiffened and reinforced square (CFST) columns respectively. The dimensions of all tested columns were considered according to European code4 [8] to avoid the possibility of overall column buckling. |
 |
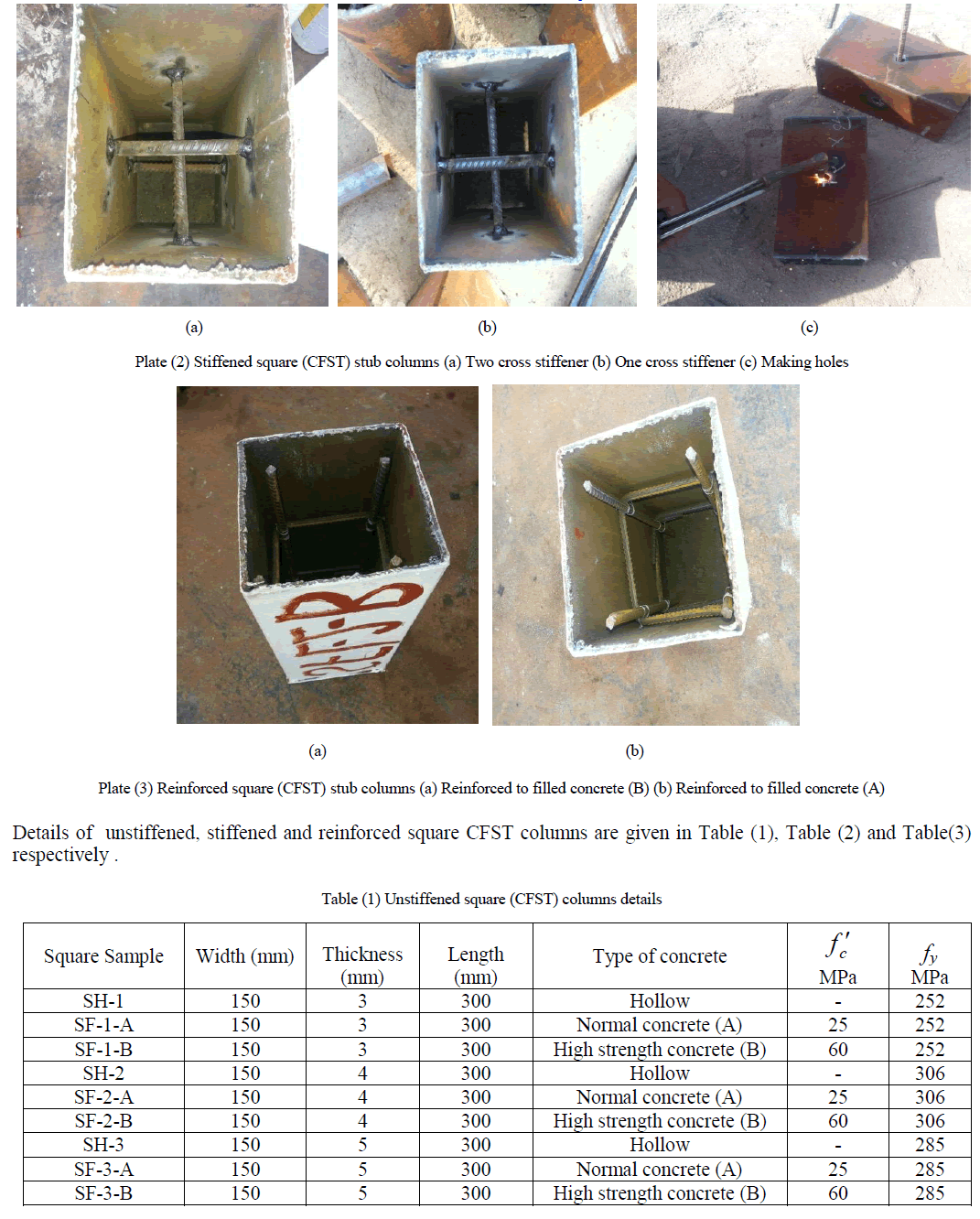 |
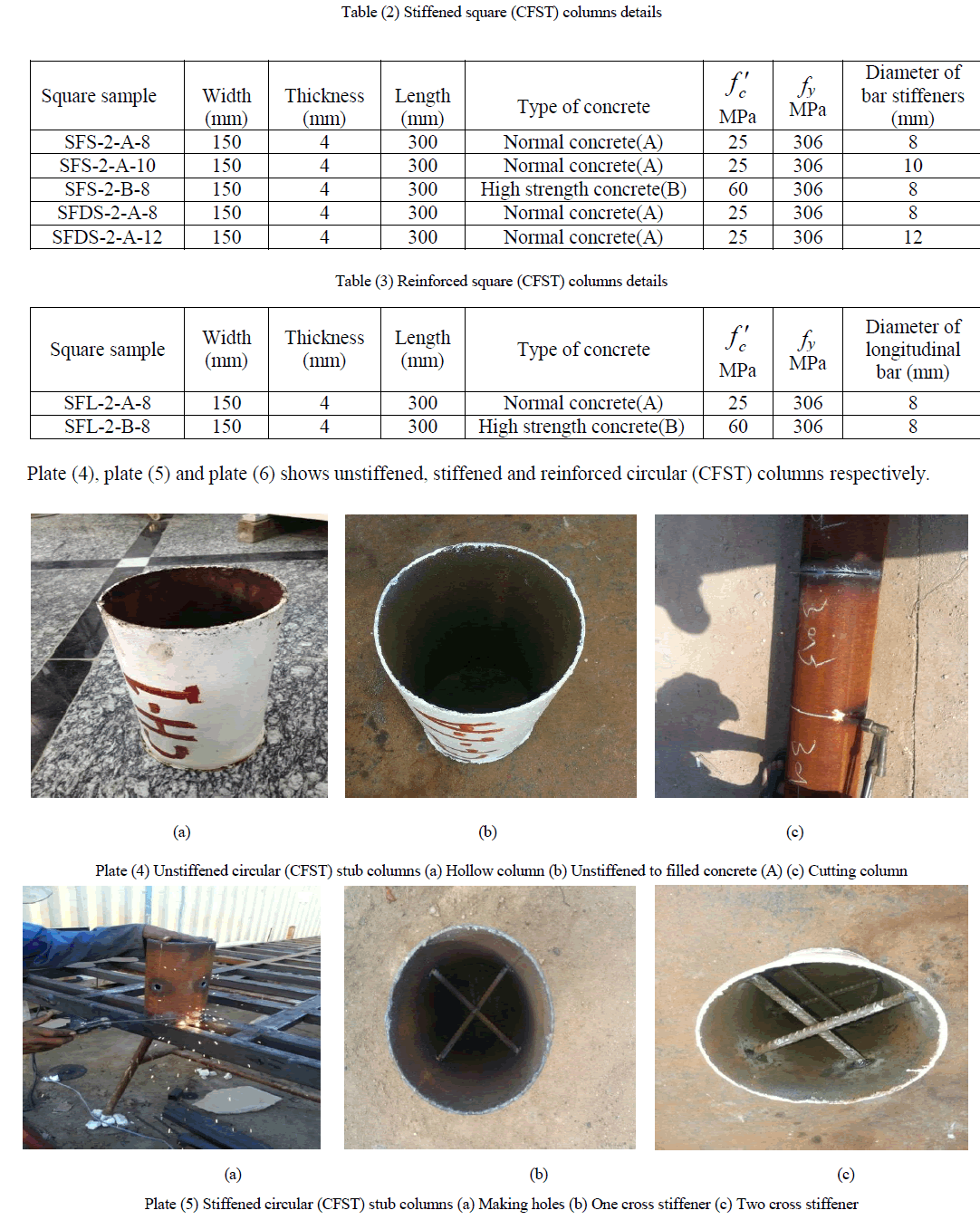 |
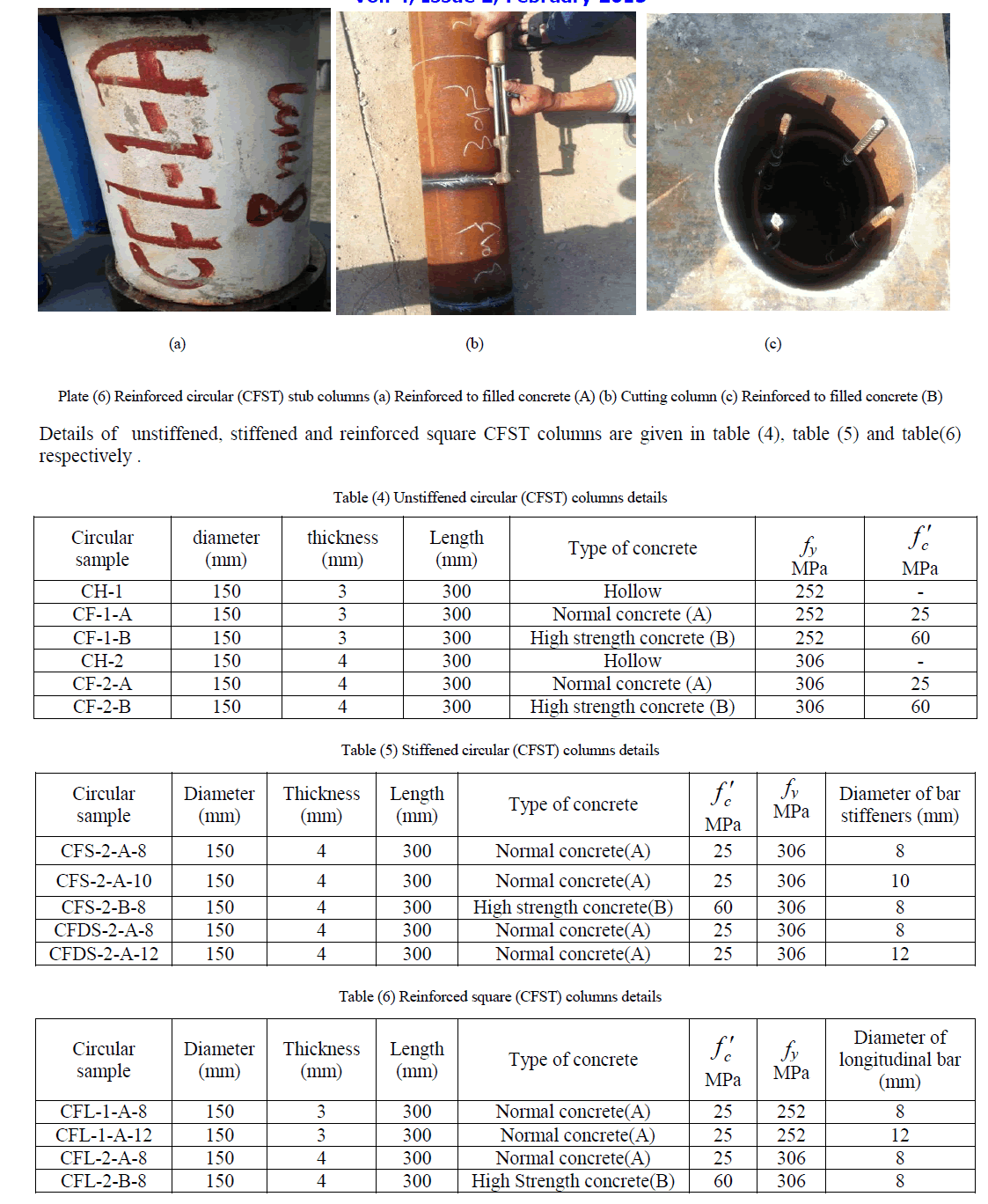 |
| Fabrication and casting of columns, All specimen arranged before casting the concrete, then concrete mix was placed and well compacted by means of iron rod, the top surface of columns was finished level. Before testing, the top surface of CFST columns were smoothened by a scraper machine to make the surfaces of concrete and steel lying on the same elevation, and therefore ensuring a transfer of load to both concrete and steel at all levels. Torsee's universal testing machine with capacity of 2000kN was used to testing columns, plate(7) shows that. |
 |
ANALYTICAL MODEL |
| The finite element method is a numerical procedure that can be applied to obtain solutions to a variety of problem in engineering. Steady, heat transfer, fluid flow, electromagnetism, linear and nonlinear problems in stress analysis may be solved using the finite element method [9]. Zienkiewicz and Cheung (1967)[10] wrote the first book which entirely devoted to the finite element method in 1967. A three dimensional nonlinear finite element analysis has been carried out to analyse all the tested (CFST) columns. The analysis was performed by using ANSYS version 12.1 computer program, verification is done to check the validity and accuracy of the finite element presentation. The accuracy of the finite element models is achieved by ensuring that the ultimate load is reasonably predicted with the experimental results. |
| To get a unique solution, the model should be constrained by using displacement boundary conditions. At y = L displacement in direction of x = y = z = zero. The displacements in the plane of loading were achieved by leaving them free, unsupported to ensure that the model acts in the same way as the experimental boundary conditions. The external applied load is represented by dividing the total load on the top nodes of the CFST columns. |
| SOLID65 (or 3-D reinforced concrete solid) element is used for the 3-D modelling of solids with or without reinforcing bars (rebar). The solid is capable of cracking in tension and crushing in compression. The element is defined by eight nodes having three degrees of freedom at each node: translations of the nodes in x, y, and z-directions. This 8-node brick element is used, in this study, to simulate the behaviour of concrete (i.e. plain concrete). SOLID45 element, an eight-node solid element was used to simulate the steel plates of CFST columns. The element is defined with eight nodes having three degrees of freedom at each node –translations in the nodal x, y, and z directions. The element has plasticity, creep, swelling, stress stiffening, large deflection, and large strain capabilities. LINK8 is a spar (or truss) element .This element can be used to model trusses, sagging cables, links, springs, etc. The 3-D spar element is a uniaxial tension-compression element with three degrees of freedom at each node: translations of the nodes in x, y, and z-directions. As in a pin-jointed structure, no bending of the element is considered. Plasticity, creep, swelling, stress stiffening, and large deflection capabilities are included. This element is used, in this study, to simulate the behaviour of steel reinforcement which works as main steel reinforcement. The geometry, node locations, and the coordinate system for all three elements are shown in figure (2). |
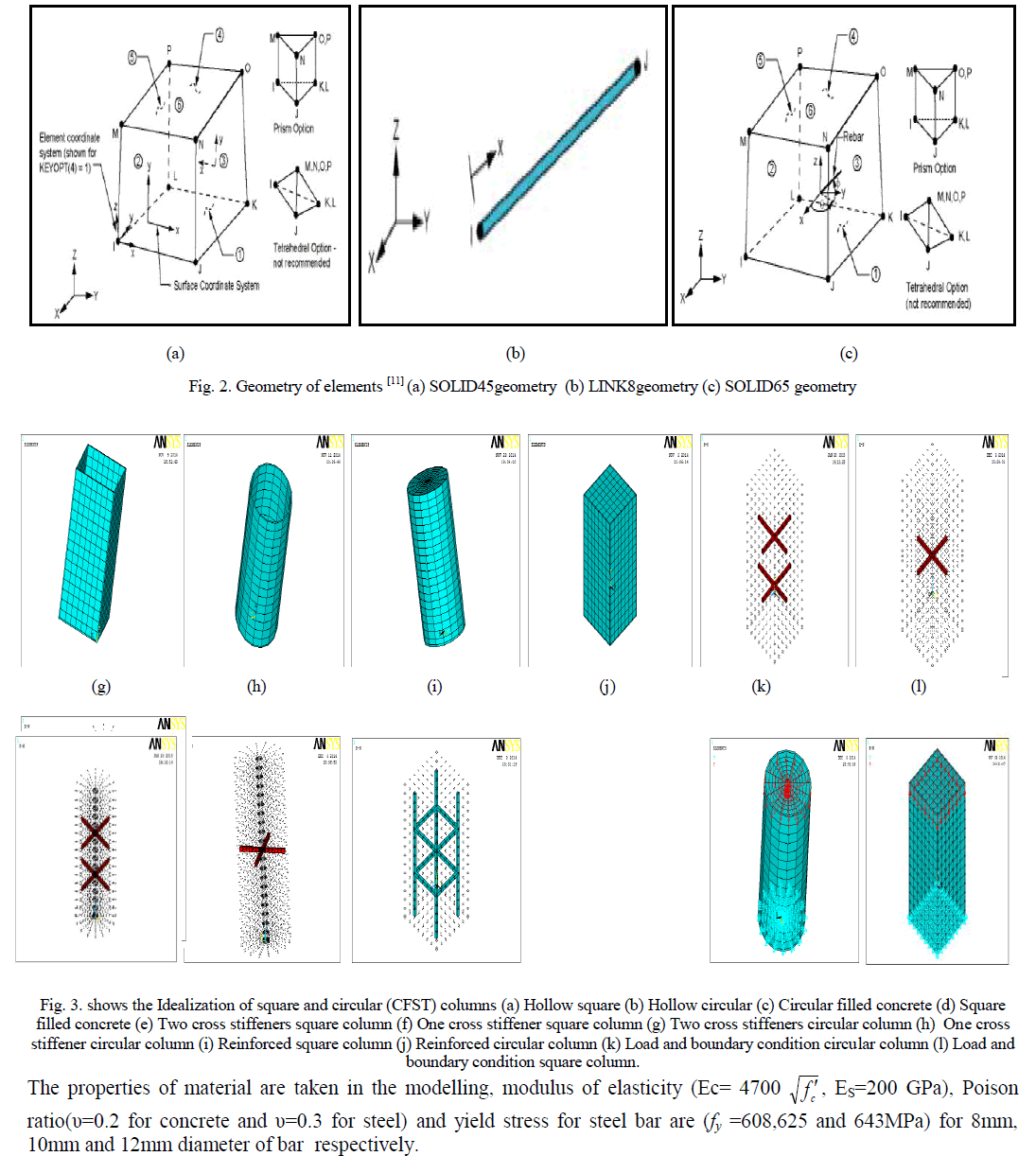 |
RESULTS AND DISCUSSION |
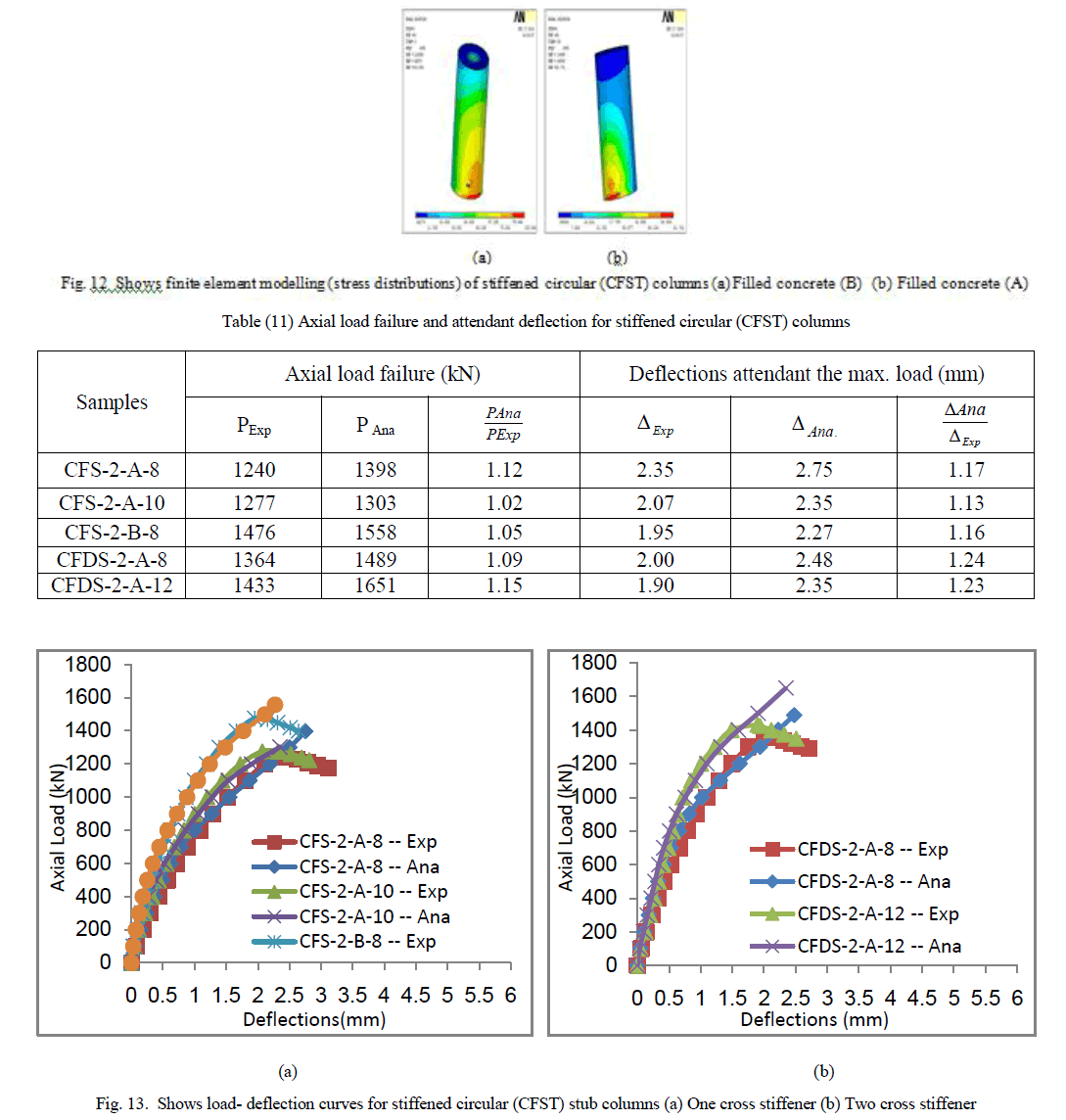
| The experimental and analytical results of the tested specimens (thirty one concrete–filled steel tube stub columns) are described. Effect of concrete compressive strength, steel tube thickness, scheme of stiffeners and longitudinal reinforcement are discussed. Plate (8) shows the unstiffened square (CFST) columns. Three dimensional finite element representation are shown in figure (4). Table (7) shows the values of axial load failure (kN) with the attended |
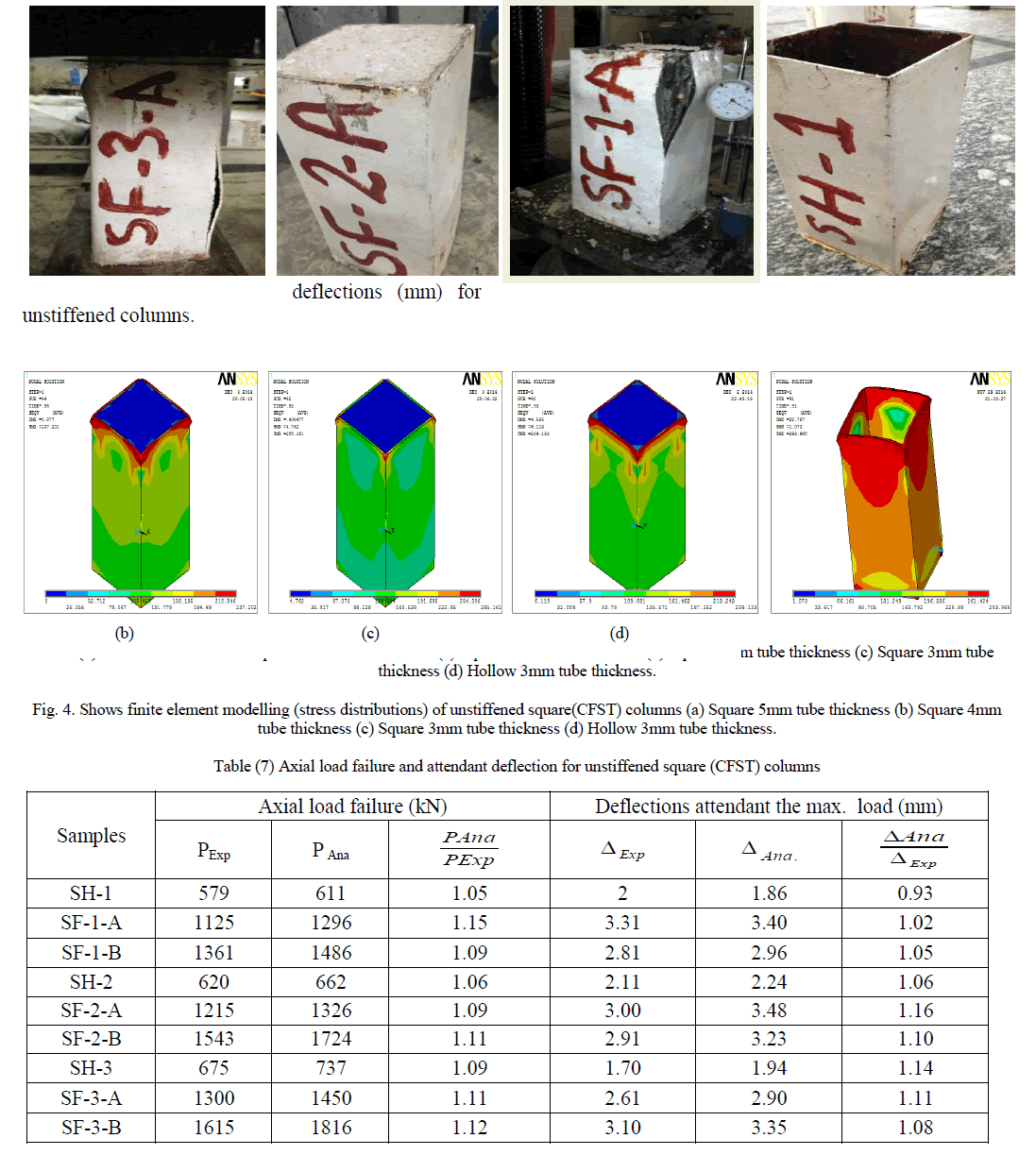 |
| From this plate it is clear that local buckling failure occurs at the column bottom, while the steel plate was splitting at the welded joints. Also it can be notice that for normal concrete, the local buckling occurs at the center and bottom of the specimen But for high strength concrete, it is obvious that no deformation appeared. From table it can be note that the value of ultimate load depends on the compressive strength. It is important to notice that the deformation depends meanly on the type of concrete. So that we can concluded that, the values of ultimate load depends on tube thickness. The failure in many types of unstiffened CFST columns occurred at the top or bottom of the specimens due to the end conditions. From the obtained results of the CFST columns, it was found that the capacity of the axial load increased when the tube thickness increased due to the confining effect of steel tube on the concrete core. The load deflection relationship for unstiffened square columns were presented in figure (5). |
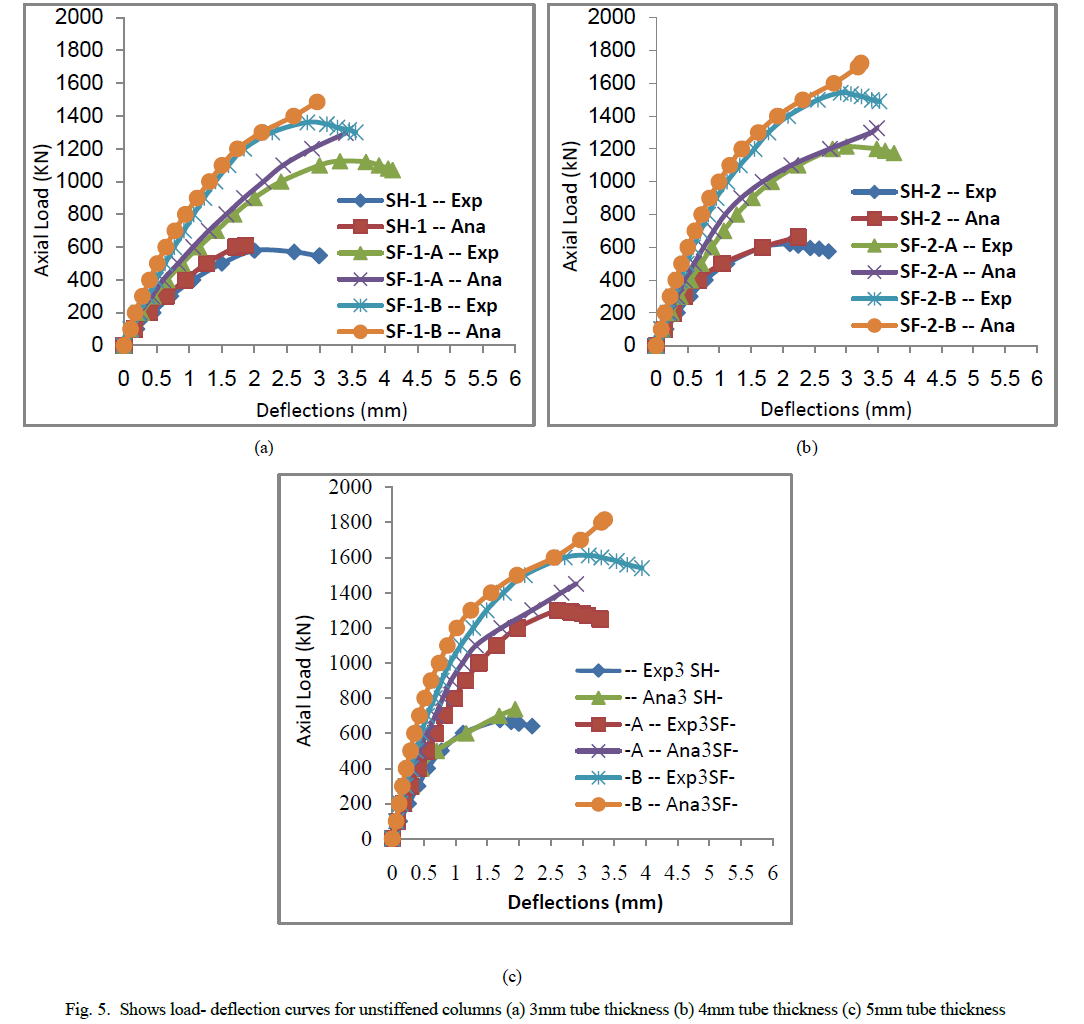 |
| From figures it can be seen that the difference between the experimental and the analytical curves are very small. While the specimens of high strength concrete gives high values of an axial load as compared with the normal concrete and hollow specimens. |
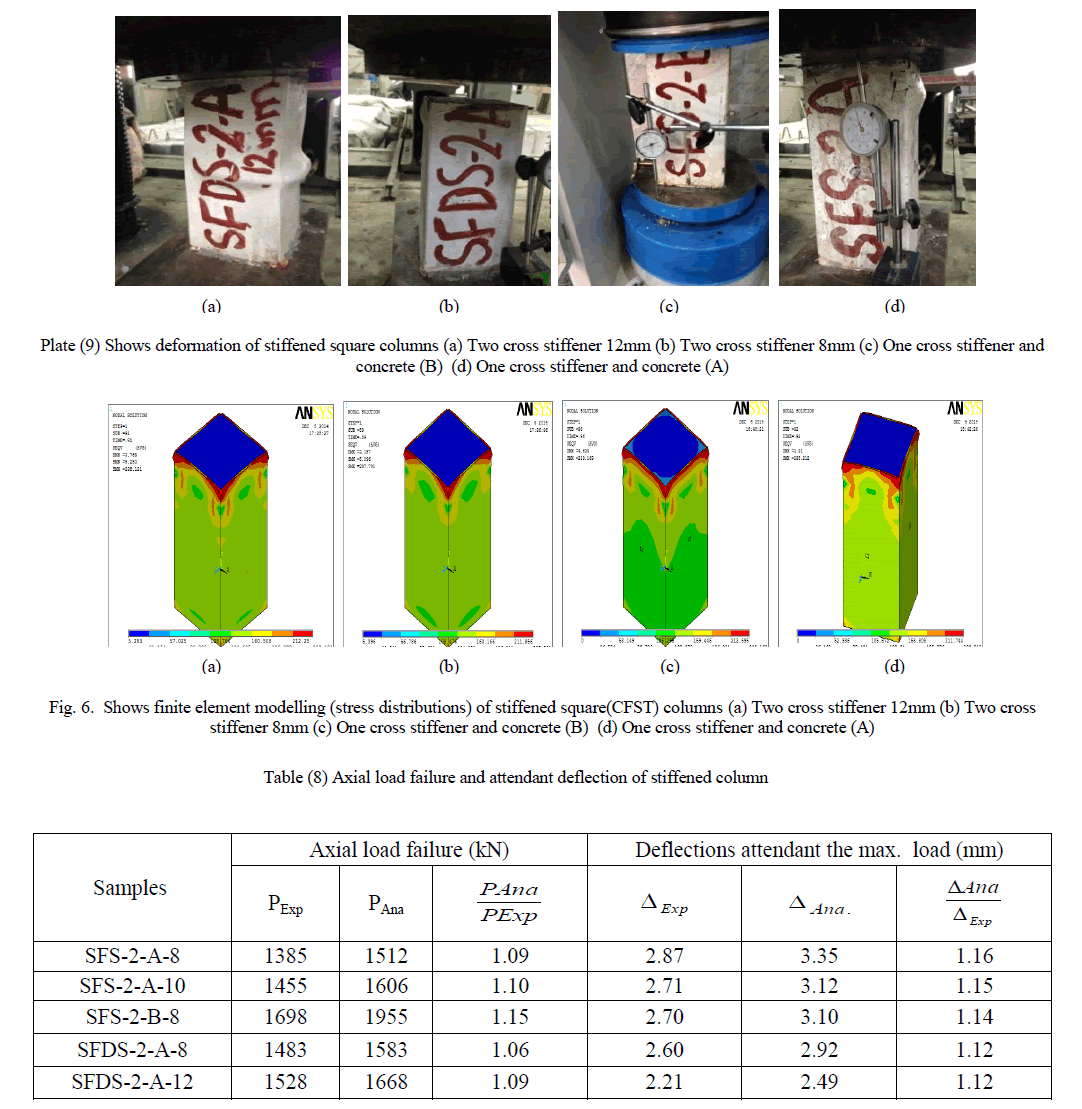
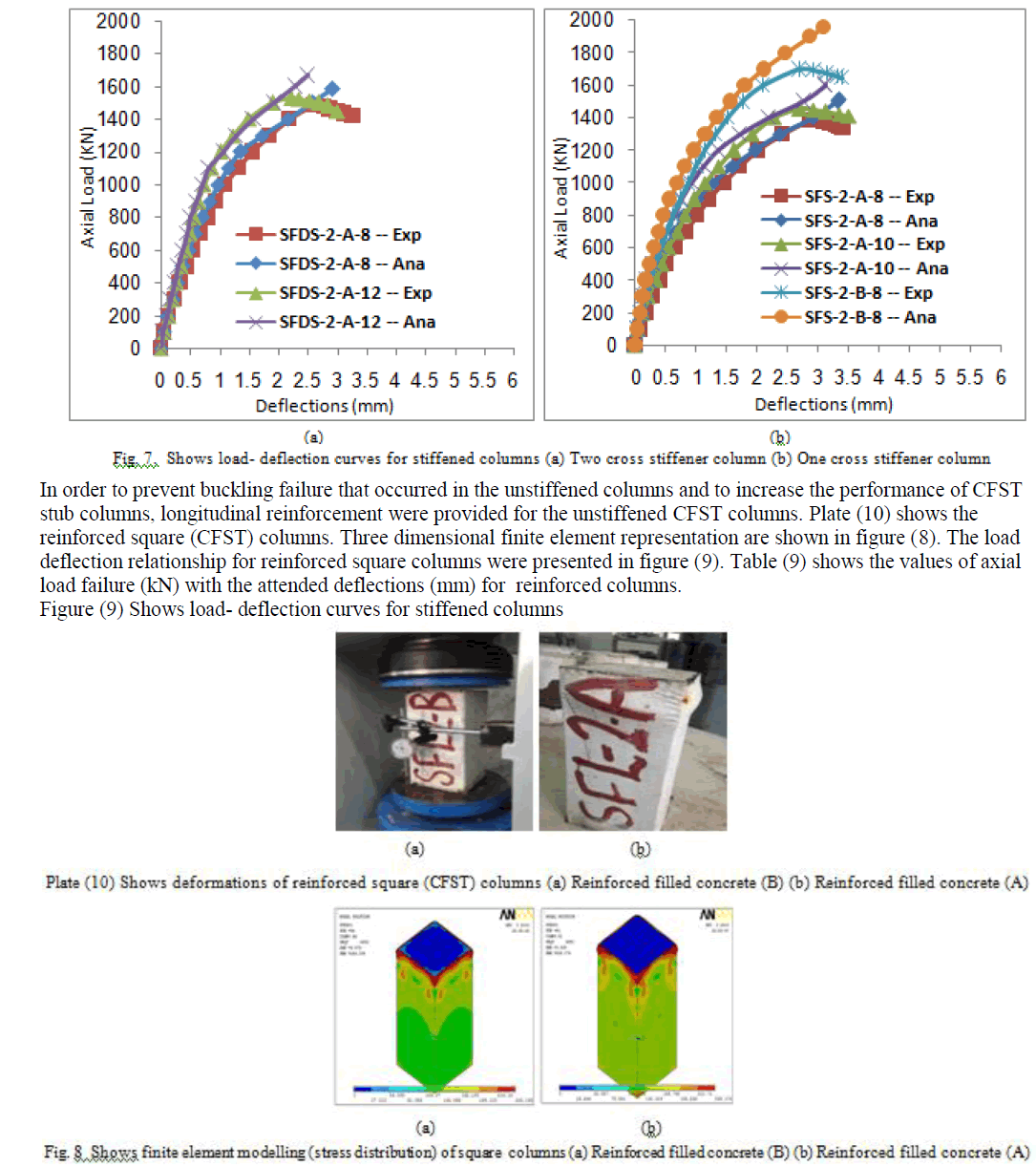
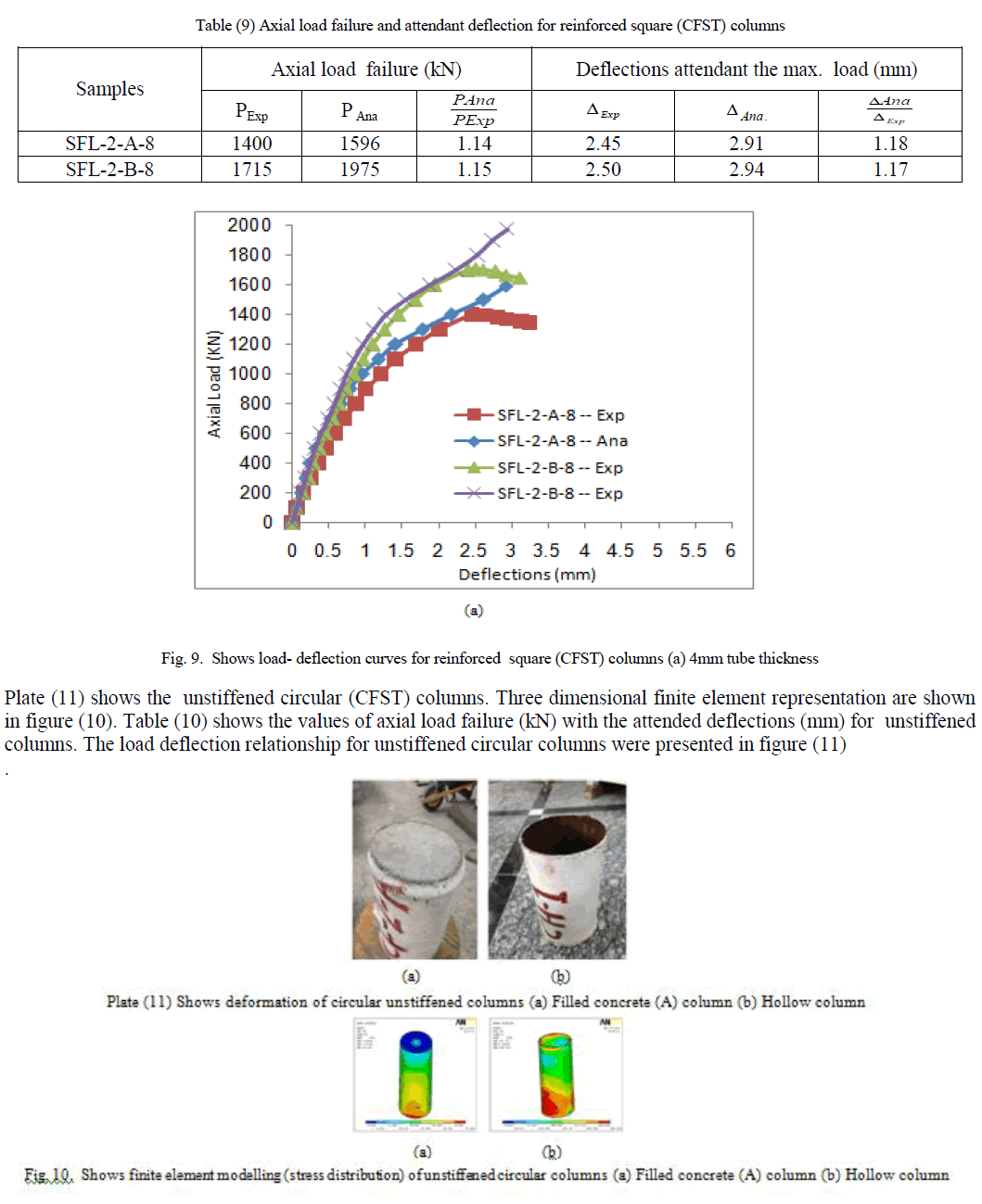
| To prevent buckling failure that occurred in the unstiffened columns and to increase the performance of CFST columns, horizontally cross stiffeners were used. The stiffeners were used in one and two layers. When one layer were used the stiffeners located at the mid-height of column, while when two layers were used the stiffeners located at third height from the top and bottom of columns. The same samples that have been studied in the unstiffened square CFST columns. But, the only different, horizontal cross stiffeners were used. Plate (9) shows the stiffened square (CFST) columns. Three dimensional finite element representation are shown in figure (6). The load deflection relationship for unstiffened square columns were presented in figure (7). Table (8) shows the values of axial load failure (kN) with the attended deflections (mm) for stiffened columns. |
 |
 |
 |
 |
 |
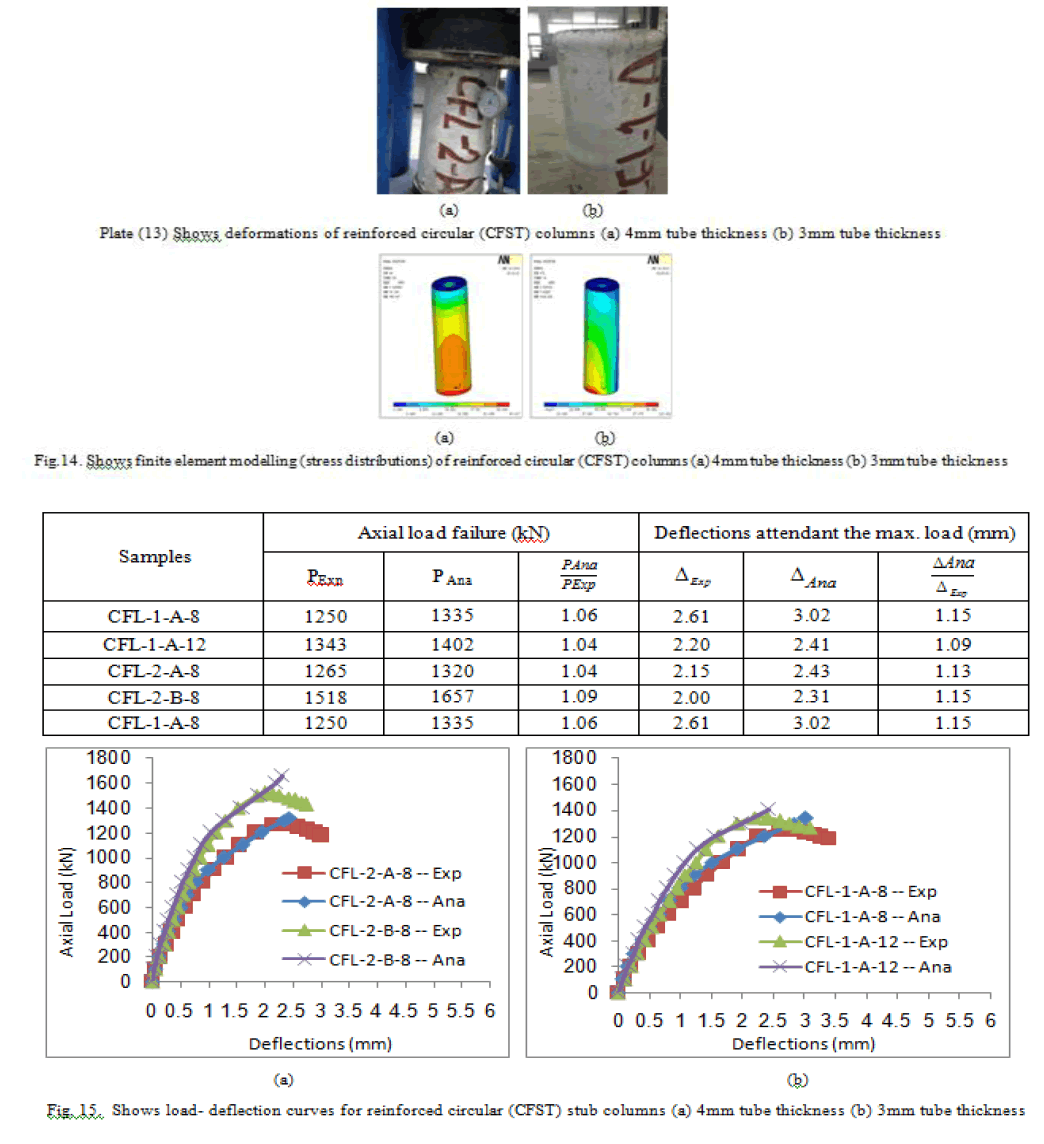
| The same samples that have been studied in the unstiffened circular CFST columns were presented in the longitudinal reinforcement circular CFST columns. Using four rebar as longitudinal reinforcement and two layers of stirrups. The longitudinal reinforcement in column was used to prevent failure buckling occurred in the unstiffened columns and to increase the performance of CFST columns. Plate (13) shows the reinforced square (CFST) columns. Three dimensional finite element representation are shown in figure (14). Table (12) shows the values of axial load failure (kN) with the attended deflections (mm) for reinforced columns. The load deflection relationship for reinforced square columns were presented in figure (15). |
 |
CONCLUSION |
| Depending on the results that obtained from the experimental and analytical work of square and circular samples. There are many facts than may be summarized as follows: |
| From experimental results, CFST columns show higher ductility after maximum load. The load can reach up to 35% of the ultimate load capacity of CFST columns, especially for reinforced and stiffened columns. The decreasing in the axial load continues until the deflection reaches about two times of the peak deflection for CFST columns. |
| The effect of (width-thickness b/t) and (diameter-thickness) ratio on ultimate strength of CFST columns will have a reverse relation. When increasing thickness of tube this ratio will decrease, then ultimate strength will increasing. The uniaxial compressive strength (f'c) has different effects on the ultimate strength of (square and circular) CFST columns; it is observed that for the same width-thickness or diameter-thickness (b/t), (d/t) ratio; the ultimate strength increases with increasing compressive strength. But that increase depends on the (width-thickness (b/t)) and (diameterthickness( d/t)) ratio, stiffener and reinforcement, as compare with the effect of tube thickness the effect of compressive strength on columns have width or diameter/thickness (b/t) or (d/t) 30 are more than for columns have (b/t) or (d/t) 50. Also effect of compressive strength on unstiffened CFST columns is more than for stiffened and reinforced CFST columns. |
| The ultimate load capacity for two cross stiffened CFST columns is more than for one cross stiffened CFST columns and more than for unstiffened CFST columns. The ultimate load capacity for reinforced (square and circular) CFST columns is more than for unstiffened (square and circular) CFST columns. |
| The buckling in the unstiffened CFST columns appeared in the top and bottom and some times in the middle of columns, but in the one cross stiffened CFST columns the buckling appeared in the top and bottom of CFST columns, because the one cross stiffener layer in the middle of columns, and when using two cross stiffener layers the buckling appeared in the middle of columns, because the two cross stiffener layers in the top and bottom of columns. Furthermore, buckling reduced in the stiffened CFST columns and when thickness was increased. |
| The filling concrete will enhance the steel carrying capacity so that all the section will reach its limit state and avoid the possibility of buckling until cracking induced in concrete at high load levels. At the same time the steel shell will confine the concrete and improve its strength and ductility. |
| Parametric studies showed that the concrete compressive strength is the important factor effecting the descending region of the load-deflection curves for all CFST columns. |
| The deformation of normal concrete at peak value is more than that for high strength concrete. |
| The result obtained from finite element analysis tests showed that the predicted load-deflection curves and the ultimate load of the tested columns are in agreement with the experimental data. |
| The initial slope of the load-deformation curves obtained by the analytical model is greater than that of the experimental work. From the stress contours obtained from the FEM analysis, it can be concluded that the stress concentrations are in the top for hollow columns and at the top and bottom for (square and circular) CFST columns. |
References |
|