ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Habeeba A1, Sabeena M.V2, Anjusha R3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The increased traffic demand, material ageing, cracking of bridge components, physical damages incurred by concrete, corrosion of reinforcement and inadequate maintenance of bridges necessitate the assessment of bridges periodically for their performances. The accuracy of analytical assessment of bridges depends on the ability of the tool to simulate the problem. The nonlinear analysis is one such tool to simulate the exact material behaviour, to evaluate strength in inelastic range. An attempt has been made to perform nonlinear finite element analysis to analyse the component of a selected road bridge. The aim of this dissertation is to study the fatigue life evaluation of reinforced Concrete Highway Bridge. Nonlinear analysis of the structural element using ANSYS is carried out. RCC T-beam Bridge has been chosen for detailed 3D nonlinear analysis. Fatigue evaluation of proposed bridge is also done using SAP-2000. Fatigue life evaluation approaches using S-N curves are also presented.
Keywords |
| Fatigue damage, Concrete bridge, Fatigue life, S-N curve, Non linear finite element analysis. |
INTRODUCTION |
| Bridges are not simply structures made out of materials, they are part of life. In many places life would be seriously disrupted, traffic would be paralysed and business would be terribly affected if the bridges fail functioning. Hence the assessment of bridges periodically for its performance turns out to be an important task. The bridge assessment can be done by conducting laboratory experiments, field tests and also through analytical means. Fatigue is a progressive deterioration of a structure by crack growth, due to a series of stress variations (cycles) resulting from the application of repeated loads, such as induced in bridge components under traffic loads and heavy vehicle crossings. Bridge decks must withstand one of the most damaging types of live load forces i.e., the concentrated and direct pounding of truck wheels. A primary function of the deck is to distribute these forces in a favorable manner to the support elements below. The current study restricts to analytical method of performance evaluation. In analytical method the accuracy of the result depends upon the ability to simulate the problem. In reality, most of the problems are nonlinear in nature. Hence nonlinear analysis is an effective tool to simulate the exact problem. Nonlinearity may be geometric or material nonlinearity. A structure could encounter either one of the above or combination of both. |
| In this study, nonlinear finite element analysis is carried out using ANSYS which employs Newton Rapson technique to solve the higher order differential equation. Elanthikadavu Bridge, a highway road bridge, situated at kodenjeri, Calicut, Kerala, India is chosen for the present study. The loads are arrived as per IRC 6-2000 standards and the responses are obtained by modelling the bridge superstructure in SAP 2000 v-14. The main objective of the study is to evaluate the fatigue life of the reinforced concrete highway bridge under moving wheel loads. |
MATERIALS AND METHODS |
| The objective of the present study was to design the deck panel and supporting girders and to find out the fatigue life of the specified reinforced concrete T-beam bridge under transient load due to moving vehicles. In this study, nonlinear finite element analysis is carried out using ANSYS for Fatigue evaluation of reinforced concrete T beam Bridge, built across river Iravinjipuya is chosen for the present study. Fatigue evaluation of bridge is also done using SAP-2000. The loads are taken as per IRC 6-2000 standards. The work in this paper is divided in two stages. 1) Bridge super structure modelling, 2) Analyse the deck panel and supporting girders and to find out the fatigue life of the specified reinforced concrete T-beam bridge under transient load due to moving vehicles. The isotropic material property for modeling the bridge is the elastic modulus (Ec) and Poisson’s ratio (ν) of the concrete and steel. Modulus of Elasticity of concrete is 25000 N/mm2 and that of steel is 2x105 N/mm2. Poisson’s ratio of concrete is 0.2 and steel is 0.3 The paper is organized as follows. Section III is description of the bridge. Section IV and V presents computer modelling of the proposed bridge. Fatigue Analysis and loading representation is given in Section VI and VII. Section VIII and IX explains fatigue analysis using ANSYS and SAP software. Section X presents analysis result. |
DESCRIPTION OF THE BRIDGE |
| It is a roadway bridge 11.05m wide, and 97.28m long straight through three main longitudinal girders and sixteen cross girders. 7.5m carriageway width and 22.3 m span RCC T-Beam bridge across river Iravinjipuza. The global method of analysis for T-beam girder bridges involves the analysis of the deck slab and the longitudinal and crosses girders. Materials used are of M25 concrete and Fe 415 steel. The bridge superstructure is 22.3m span simply supported, cross sectional dimensions of the bridge is as shown in the Figure 1. |
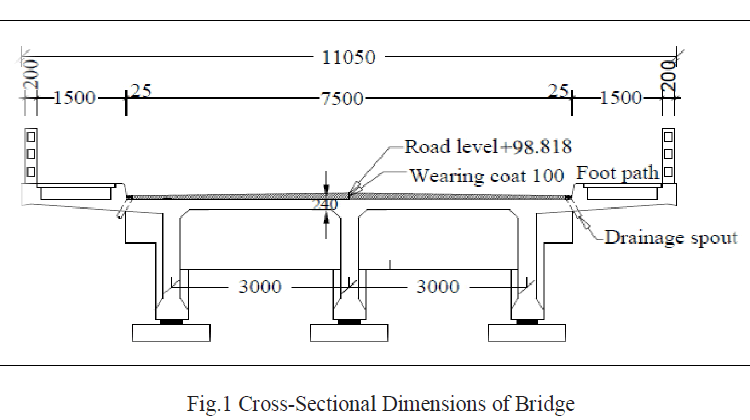 |
COMPUTER MODELING USING ANSYS |
| The whole bridge is first modeled in CATIA (Computer aided three dimensional interactive application) software and then importing the model to ANSYS workbench and then importing the model to ANSYS Mechanical APDL. Finite Element Analysis (FEA) represents a numerical method, which provides solution to problems that would otherwise be difficult to obtain. The numerical analysis investigations were performed with commercial software ANSYS 14.5. Modelling the complex behaviour of reinforced concrete, which is both non homogeneous and anisotropic, is a difficult challenge in the finite element analysis of civil engineering structures. Where a special three-dimensional eight nodded solid isoperimetric element, Solid 65 is developed. It models the nonlinear response of brittle materials and is based on a constitutive model for the triaxial behaviour of concrete. Solid 65 allows the presence of four different materials within each element; one matrix material (e.g., concrete) and a maximum of three independent reinforcing materials. The concrete material is capable of directional integration point cracking and crushing besides incorporating plastic and creep behaviour. The reinforcement (which also incorporates creep and plasticity) has uniaxial stiffness only. In the current study, Solid 65 element available in ANSYS is employed for obtaining the ultimate load carrying capacity and for determining the behaviour of concrete bridge under service load.. |
REINFORCEMENT MODELING |
| There are two techniques to model steel reinforcement in finite element models for reinforced concrete. The discrete model and the smeared model. The reinforcement in the discrete model uses bar or beam elements that are connected to concrete mesh nodes. The concrete and reinforcement share same nodes and concrete occupies the same regions as the reinforcement. A drawback to this model is that the concrete mesh is restricted by the location of the reinforcement and the volume of the mild-steel reinforcement is not deduced from the concrete volume. The smeared model overcomes the concrete mesh restrictions. The smeared model assumes that reinforcement is uniformly spread throughout the concrete elements in a defined region of the FE mesh. This approach is used for large-scale models. Here smeared model of reinforcement is used. |
| For smeared model, parameters to be considered are material number, volume ratio, and orientation angles (θ and Φ) in X and Y directions respectively. Table 1 shows Real constants used for bridge slab. Rebar1, 2 and 3 mentioned in Table 1 refer to vertical, horizontal and shear reinforcements. Volume ratio refers to the ratio of steel to concrete in the element. |
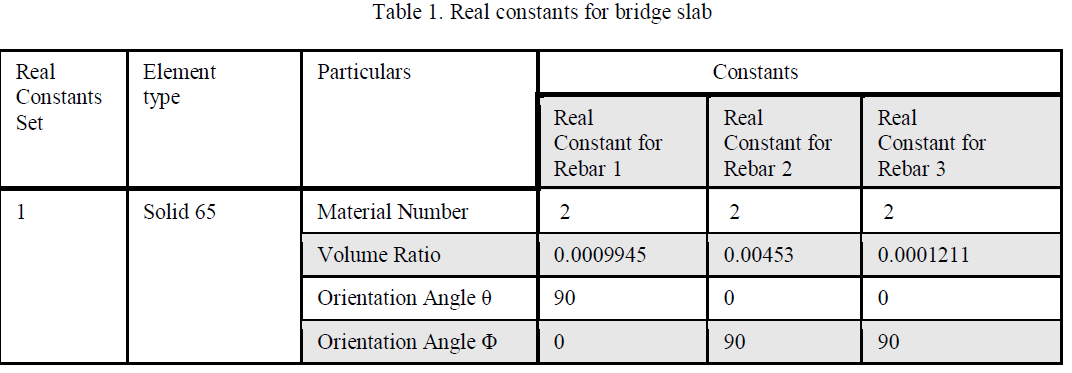 |
LOADING REPRESENTATION |
| Non linear analysis of bridge model was carried out under the simulated wheel load of IRC Class A wheeled vehicle as per IRC 6−2000. Special technique is employed for representing a moving load or a vehicle. This method uses the transient solution analysis of the ANSYS, placing the loads on one specified set of nodes at a time. The program divides the axle weights in half and applies two wheel loads at a distance equal to half the vehicle width onto either side of the centreline of vehicle travel. Figure 2 shows IRC Class A train of vehicle. Accumulating fatigue damage caused by passing vehicles is needed for fatigue safety evaluation of existing concrete bridges. The fatigue life can also expressed in terms of number of years. The design traffic is considered in terms of cumulative number of standard axle. Cumulative number of standard axle is computed as per IRC 37 (2001). The following points are considered. |
| I. Axle loading will be used for the calculation of stress ranges as per IRC –Class A loading. |
| II. For simplifying the number of cycles per vehicle will be assumed equal to one cycle per truck |
| III. The value of average daily truck traffic (ADTT) was assumed less than 5228 truck/day. |
| IV. The growth factor is assumed as 6-7.5% for road bridges in rural areas. |
REMAINING FATIGUE LIFE |
| Remaining fatigue life is find out by two ways |
| 1. Fatigue evaluation based on S-N curve. Here S-N curves for RCC bridges, which were proposed by ASHTO, are used in estimating the remaining fatigue life. The fatigue damage caused in the bridge is computed by using ‘Palm-gren Miner’s theory of linear damage accumulation. According to Miner linear fatigue accumulative damage, fatigue damage can be calculated by: |
| The total damage to the structure is given by D= Σ ni/Ni. |
| ni = Observed number of stress cycles for different stress ranges |
| Ni = Theoretical number of stress cycles corresponding to observed stress ranges from S-N curve. |
| i = 1,2,3 …. Up to n stress ranges |
| For the current study the S-N curve was obtained using the ASTHO code.6.6.1.2 |
| 2. By checking the deflection values of deck slabs and supporting girders that failed the permissible deflection limit. The deflection values are obtained from SAP-2000 software. The deflection for all the load cases met the limit specified by IRC 24 (IRC 2001), which states that the total deflection caused by dead load, live load, and impact should be less than 1/600 of the span. |
FATIGUE ANALYSIS USING ANSYS |
| Fatigue is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading.. Fatigue occurs when a material is subjected to repeated loading and unloading. Fatigue life is defined as the number of stress cycles of a specified character that a specimen sustains before failure of a specified nature occurs. When the cyclic stresses are below certain value (termed as fatigue limit /endurance limit), cracks do not initiate. But, if the cyclic stresses are above the fatigue limit, cracks initiate after a certain number of cycles and then grow at a progressively increasing rate until complete fracture occurs. S-N curve has been used for conducting a fatigue analysis. |
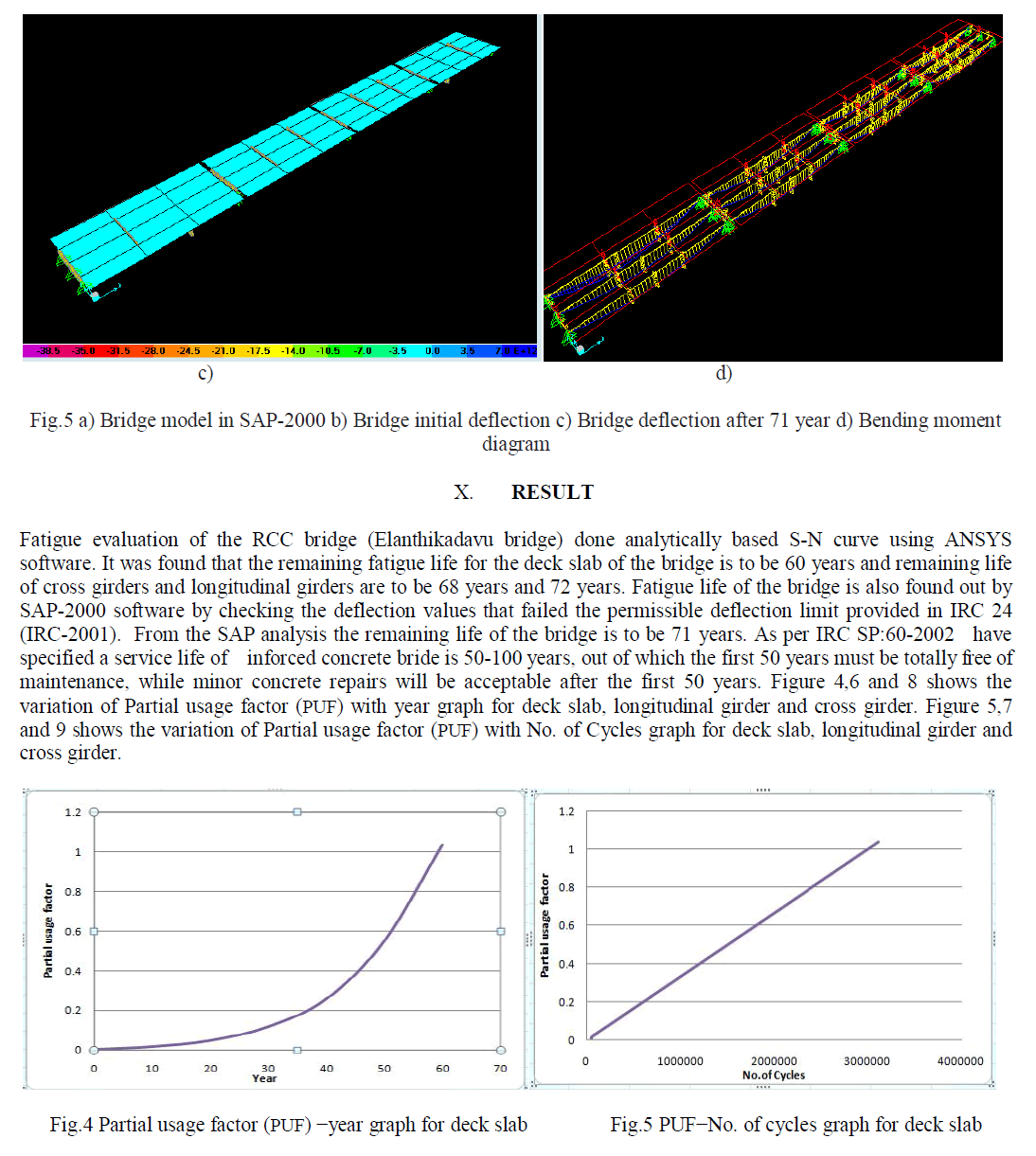
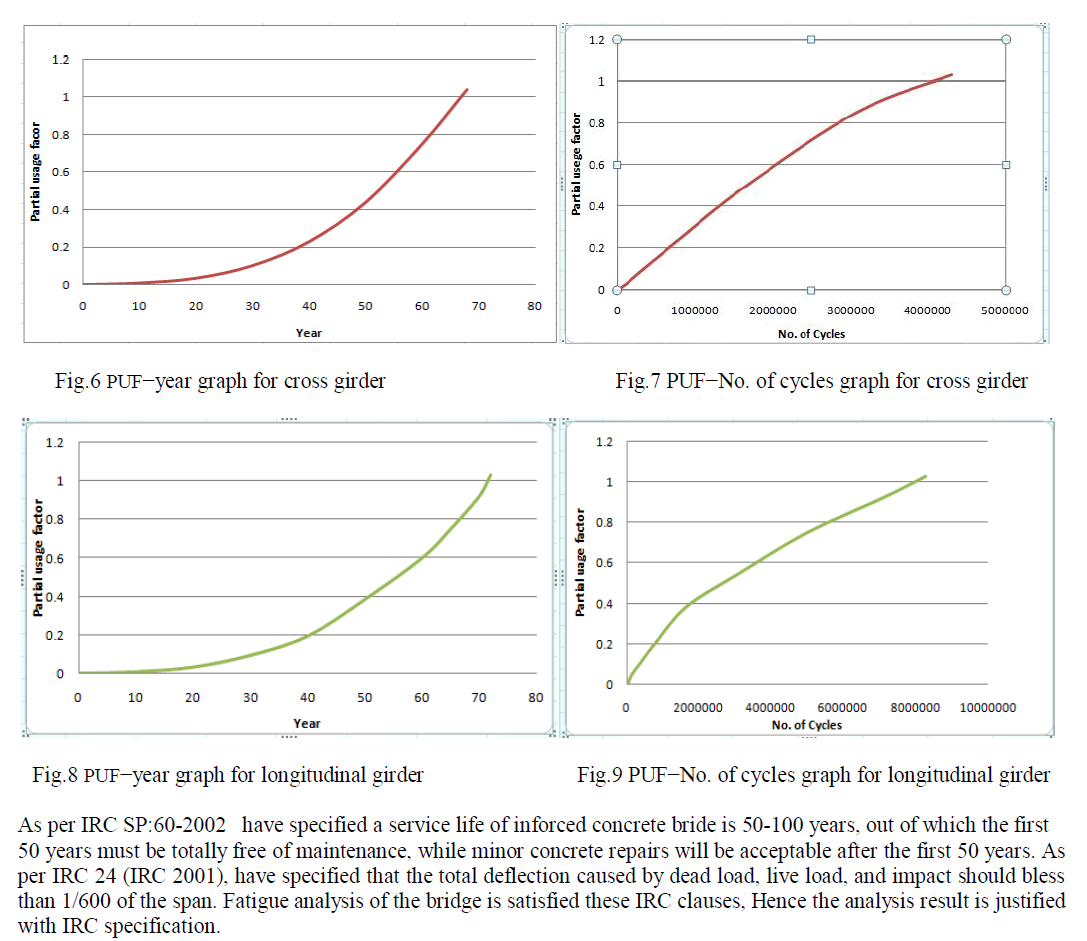
| A single span of the bridge is taken for detailed analysis. Then meshing is done using volume sweep meshing. Total number of node is 363355. After meshing loading is applied as per IRC Class A and placing the loads on one specified set of nodes at a time. Analysis done as the static non linear analysis of ANSYS. The first part of analysis calculates the member deflection and stresses for the model configuration used. The second part, fatigue analysis of bridge is done, by applying the number of cycles at each year. S-N curves for RCC bridges, which were proposed by AASHTO, are used in estimating the remaining fatigue life. Stress and corresponding number of cycles values obtained from S-N curve are applying to fatigue property table in ANSYS Mechanical APDL. After fatigue analysis we got a fatigue usage factor or partial usage factor, whenever the partial usage factor > 1 the fatigue failure of the bridge occur. Maximum stress coming node in deck slab, longitudinal girder and cross girder is taken fatigue analysis. Figure 3 shows Fatigue analysis result of deck slab after 60 year. After 60 years number of cycles becomes 3.11x106 /day and partial usage factor of deck slab is 1.03667. From the analysis fatigue life of deck slab is 60 year. Figure 4 shows bridge model in ANSYS and Bridge displacement and maximum stress location. |
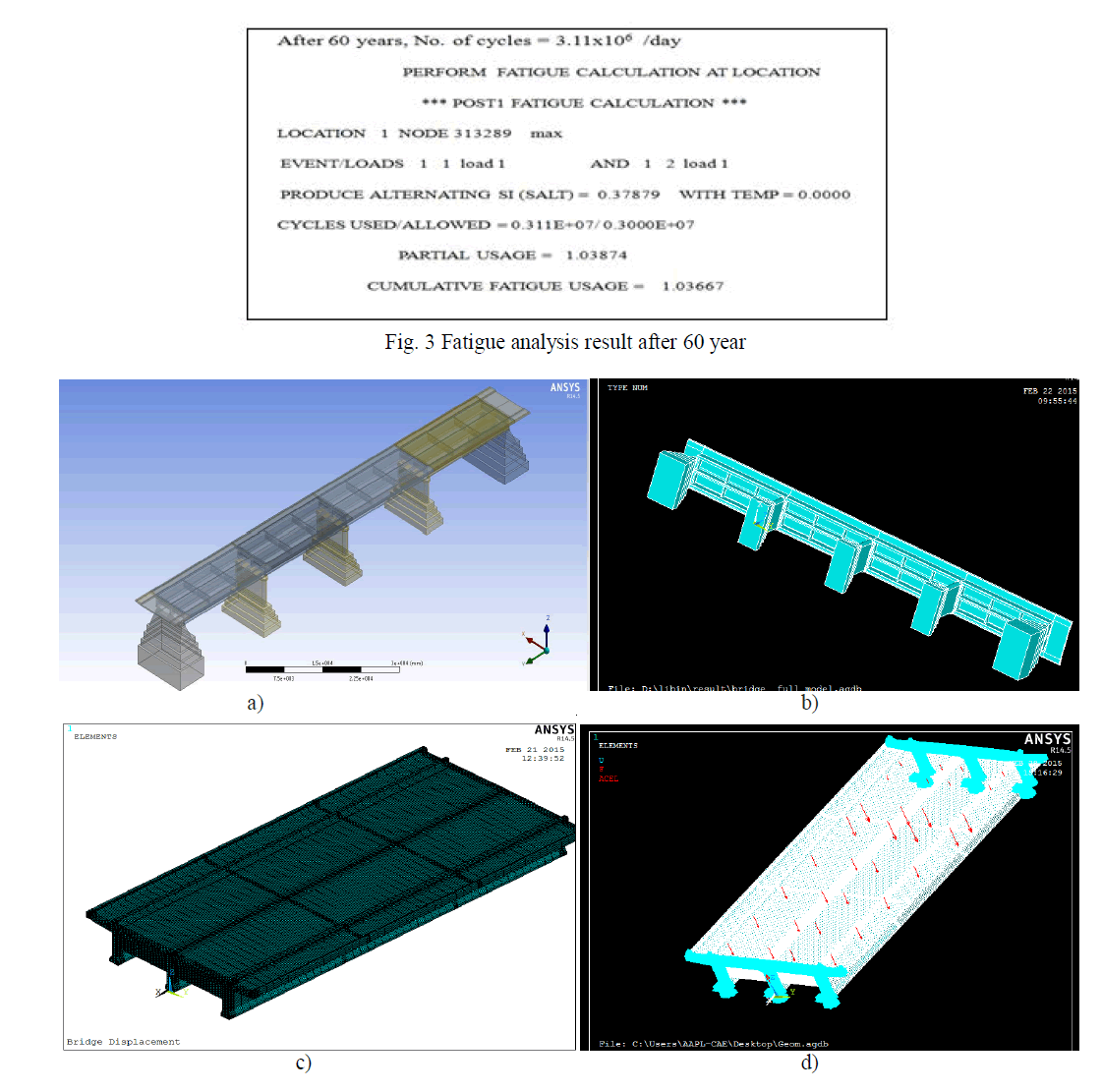 |
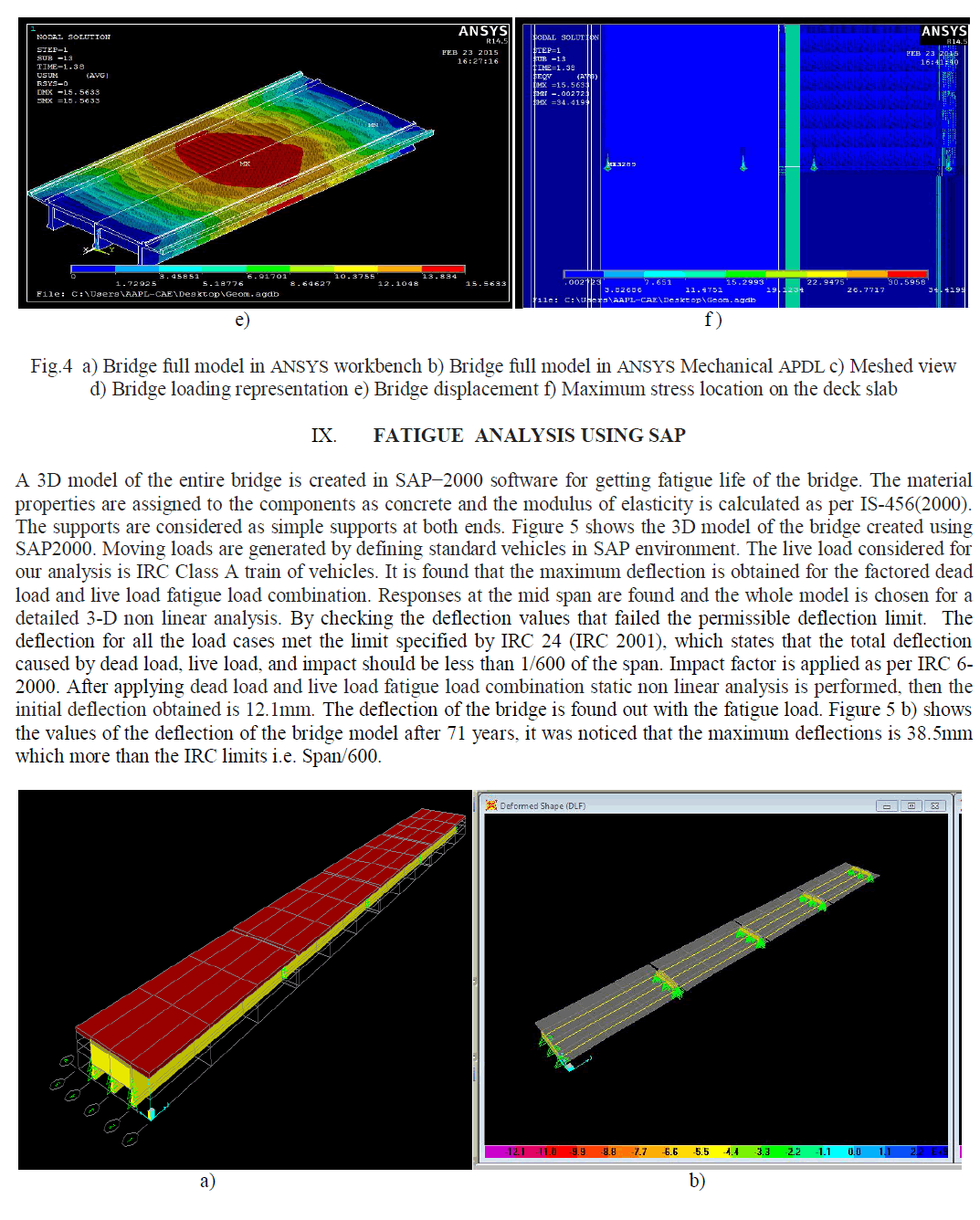 |
 |
 |
CONCLUSION |
| An evaluation of remaining fatigue life for reinforced concrete bridge was carried out under a given moving wheel load. The remaining fatigue life for the deck slab of the bridge is to be 60 years and remaining life of cross girders and longitudinal girders are to be 68 years and 72 years respectively. |
References |
|