F-(En-8) by K3 is Computable in Donald-Thomas in Variants for an Homomorphisme Stablished in L by Grigorchurt Fields

Introduction

By each coding resource in L exists in En-8 an automorphisme such the homological vertex that identifying by sunsets in C/C++ such in {F-(En-8) by K3 is computable in Donald- Thomas in variants for aun homomorphism in the form {Ln-8 vertex in Grigorchurt-torsion}

The vortex of this mode identifying in K3 correspondant to by the same form in {Ln-8 vertex in Grigorchurt-torsion} and existed in the hardness vortex fluids that are produced turbulences in the transformed in lie groupies in the atmosphere. The foliations produce in an idehomorphisme comparable to lay groups and the geometry and number theory in such product of En by lie groupoides comparables to hardess fields (Grigorchurt fields in L in En-8).

A serie of numerical sets dues by a series of random numbers f=(0.1,..a,n) are correspondant with a series of a reduces series of wavelets in the form Γ(1)=SL2(n, R) and ¯Γ in a simple denotation his conjugation image in the other side of the upper hal-plane, that represented predicament this sheaves surfaces G=SL2(n,R), H=G/H that is a modular form or in that the at a Labelian group. (Geometry and number theory)

Edit series numbers:

DESCRIPTION

The Erschler integral ours proportionated at viceverse process a polynomial in the same form (integrated or deriving this protocol by Fortran 77, 90 or successive) the same are by series numbers in a numerical topology in logic operations.

Edit topological wavelets:

Structure constants

A finite dimensional Lie algebra is characterized, relative to a basis, by a set of numbers, called structure constants that specify the bracket operation. Thus if {v1,…,vn} is a basis of a Lie algebra V, we define the structure constants ckij, (i,j,k=1,…,n) by expanding, in terms of this basis, the bracket of any two basis elements of En over Jc^* in K where is computable.

A subspace Jc^* take the form W(i,k)=J{ik1,ik2...ikn) where are established a series of hardness manifolds some Grigorchurt and where in En-8 computable by K3 stablished the Lie groups abelians and Donald-Tomas invariants computables in K3 by Wn-8 dimensional.

The Landau-Lifshitz in quantum field provided the basis by understand the principals theory of Einstein’s gravity in order to explain the notion of energy momentum pseudotensor in quantum fields (K-moduli spaces), of such equivariant quantum Schubert calculus for G/P In a Z2 filtered algebraic structure (in that the at an algebraic structured in polynomials) and a “quantum to classical” principle on the torus equivariant quantum cohomology of a complete flag variety of general Lie type, generalizing earlier works of Leung and the second author.

The Landau-Lifshitz in a quantum field are supported in his mathematics structure the structure of various applications one quivariant quantum Schubert calculus, including an equivariant quantum Pieri rule for partial flag variety F(1fi,2fi nfi).

A subspace Jc^* take the form W(i,k)=J{ik1, ik2...ikn) where are established a series of hardness manifolds some Grigorchurt and where in En-8 computable in the same mode of some are realizated by K3 established the Lie groups abelians and Donald-Tomas invariants computables in K3 by Wn-8 dimensionals.

In G(n), integers a,b are connected if a|b or b|a and where in H(n), or in that the at Hilbert spaces is applied to Lie group representations, that idea is called gemetric quantization. Laplace transforms method for constructing universal invariants of 3–manifolds. As an application, we recover Habiro’s theory of integer homology 3–spheres in a manifold in x by Laplace transform in u(x) and extend it to some classes of rational homology 3–spheres with cyclic homology that are produced in quantum invariants where are developed the Schorodinger equation.

Hamiltonian structures in geometry invariants of lie groups or in that the at G system mechanics, response to from the study of specific representations to an attempt to give a general method for constructing Lie group representations. The idea in question sometimes is called “geometric quantization”.

Starting from a classical mechanical system with symmetry group G, the responding quantum mechanical system will have a Hilbert space C* carrying a unitary representation of G system mechanics. G system mechanics carrying to idea of a particle moving in a geometric quantization some occurs in the thermos dynamics systems which the most simple form is defined by Poisson or by the thermos dynamics laws that in this Lie groups (geometry invariants) corresponded with the moving of a particle.

CONCLUSION

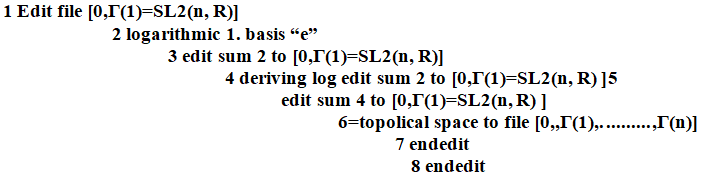
The set of possible unit sphere topologies in G1 are combinatorial invariants of the complex G, and establish so that also the green function range of G is a combinatorial invariant. The unit sphere character formula g(x,x)=i(x) applies especially for the prime graph G(n) and prime connection graph H(n) on square free integers in {2,...,n} playing the role of simplices.

Computables some we are provided by the Erschler integral for topological spaces of En-8 dimensional spaces in the form describe transformed by smooth logarithmics this numbers theory by in the polynomials G (1ki, 2ki,…,nki) where “k” are functions in Brevin notation.