Fractional Order PID Controller Based
Bidirectional Dc/Dc Converter

K.Giridharan; A.Karthikeyan

Fractional Order PID Controller Based Bidirectional Dc/Dc Converter

K.Giridharan ¹,A.Karthikeyan²

PG Scholar, M.E. – Power Electronics & Drive, PSNA College of Engineering & Technology, Dindigul, India
Associate Professor, Department of EEE, PSNA College of Engineering & Technology, Dindigul,India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In this project, the auxiliary switch control using a lookup table using FO-PID is proposed to enhance the efficiency of the bidirectional DC/DC converter used in electric vehicle, which performs soft switching. Continuous current data are difficult to obtain during a resonant operation due to the limit of ADC capacity. The control method properly controls the auxiliary switch turn-on time according to the required load current; this auxiliary switch control brings the more efficient control in generative and regenerative mode operation. This work proposed a design methodology of auto-adjustable PI controller using Artificial Intelligent controller technique. The proposed AI method can adjust the controller parameters in response to changes in plant and disturbance that specifies properties of the desired control system. In order to analyze the performances of the proposed system using PI controller tuned with Improved Particle Swarm Optimization algorithms. The work has been implemented with MATLAB / Simulink 7.13 software environment.

INDEX TERMS

Fractional Order Proportional Integral Derivative, Improved particle swarm optimization, soft switching, bidirectional converter, auxiliary switch control.

INTRODUCTION

The environmental and economical benefits from commercial electric vehicles have stimulated global interest in developing electric vehicles. To improve the efficiency of electric vehicles, the auto industry has financially invested significantly in batteries, various types of charging equipment’s, inverters and bidirectional dc/dc converters, and traction motors for EVs. Among them, various topologies for the bidirectional dc/dc converter have been proposed for many EVs [1]–[10]. The bidirectional dc/dc converter on board electric and hybrid vehicles should boost the low voltage of batteries to the high voltage of the inverter dc-link [4]. It should also be operated in the buck mode to charge the battery bank with regenerative energy during vehicle deceleration and braking. The importance of a bidirectional dc–dc converter is getting increased. Because the structure of the converter is simple, and its control is comparably easy, it is used as the topology of conventional bidirectional converter. However, the drawbacks of the conventional bidirectional dc–dc converter are the large switching losses and the long reverse recovery time of antiparallel diodes. Particularly, during the reverse recovery time of the diodes, it can be caused of circuit damage and electromagnetic interference problems due to high current spikes. Thus, in order to improve the shortcomings of conventional pulse width modulation (PWM) methods, and increase the efficiency of the system, the study using series resonance, parallel resonance, and quasi-resonance methods have progressed [11], [12]. However, due to the common characteristic of resonant converter, lots of conduction losses occur because of high circulating energy. To overcome the drawbacks of the resonant converter, the zero voltage transition (ZVT) and zero current transition (ZCT) methods are proposed [13]–[16]. The ZVT and ZCT methods are that switches turning ON and turning OFF under zero voltage and zero current condition using resonance. The ZVT and ZCT methods can be applied to the conventional bidirectional dc–dc converter through adding auxiliary circuit to the converters. However, since the added auxiliary circuit is operated under hard-switching condition, the other losses occur [13]. Moreover, lots of other circuits are weak in high resonant current and voltage, and the range of load for resonant circuit is limited. The composition of the proposed resonant bidirectional dc/dc converter is an auxiliary circuit added form to the conventional bidirectional buck–boost converter. The fundamental operation equals the conventional bidirectional buck– boost converter [18]–[20]. The resonance of the proposed converter is caused by the resonant capacitor and inductor of the auxiliary circuit. The auxiliary switch is operated in boost mode and buck mode. The soft switching is carried out by the main switches, diodes, and auxiliary switches.

To perform the soft-switching action, the conventional control method has to calculate the time difference between the gate signals of the main and auxiliary switches. The aim of this work is to introduce the auxiliary switch turn-on time control for the bidirectional dc/dc converter in an electric vehicle system.

OPERATION AND ANALYSIS OF THE PROPOSED CONVERTER

A.PROPOSED CONVERTER CONFIGURATION

Fig. 2.1 shows the proposed bidirectional softswitching dc–dc converter, which is formed by adding one resonant inductor, two resonant capacitors, and two switches to the conventional bidirectional converter circuit. The soft-switching operation occurred by energizing Lr in the auxiliary circuit with the voltage difference Vhigh−Vlow just before turning ON the main switch. In order to maintain the voltage across Lr with Vhigh−Vlow before the main switch is turned ON, the upper converter should be operated in continuous conduction mode.

OPERATION MODE:

MODE 1 (t0≤t<t1):At t=t0, both switches S1and Sa1are in turn-off state. When the Sa1is turned ON, mode 1 is started. Since the resonance of Lr, any current is not flowing through Sa1, and the switch is turned ON under the ZCT condition. During this mode, iLr is increased by the current flowing through Lm and the antiparallel diode of Sa2, and it can be described as (1)–(5). When the same amount of current is flowing though Lm and Lr, this mode is finished.

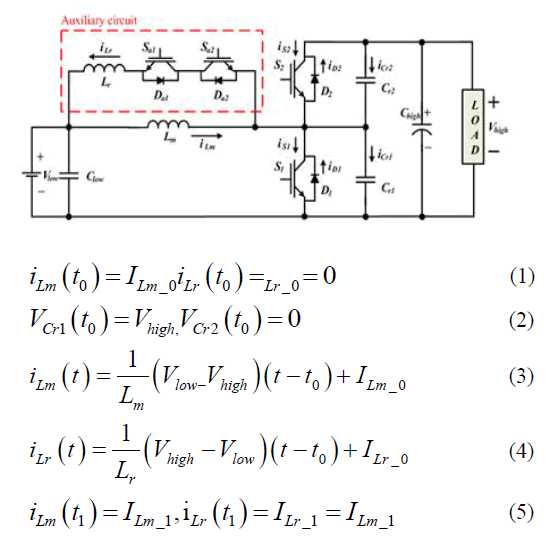MODE 2 (t1≤t<t2): When iLr is larger than iLm, mode 2 begins. Due to the continuity of iLr, the resonance between S1 and the output capacitor of S2 is started. Two switches S1 and S2 are in turn-off state, and as the capacitor Cr1 is charged and discharged iLm and resonant capacitor current flow through Lr. As a result, the voltage across S1 and S2 is decreased and increased complementary due to the resonance. It can be described through (7). When the voltage acrossS1 becomes 0V, and that of S2 is equal to Vhigh, the resonance between Cr1and Lr is finished. Moreover, iLr is getting decreased.

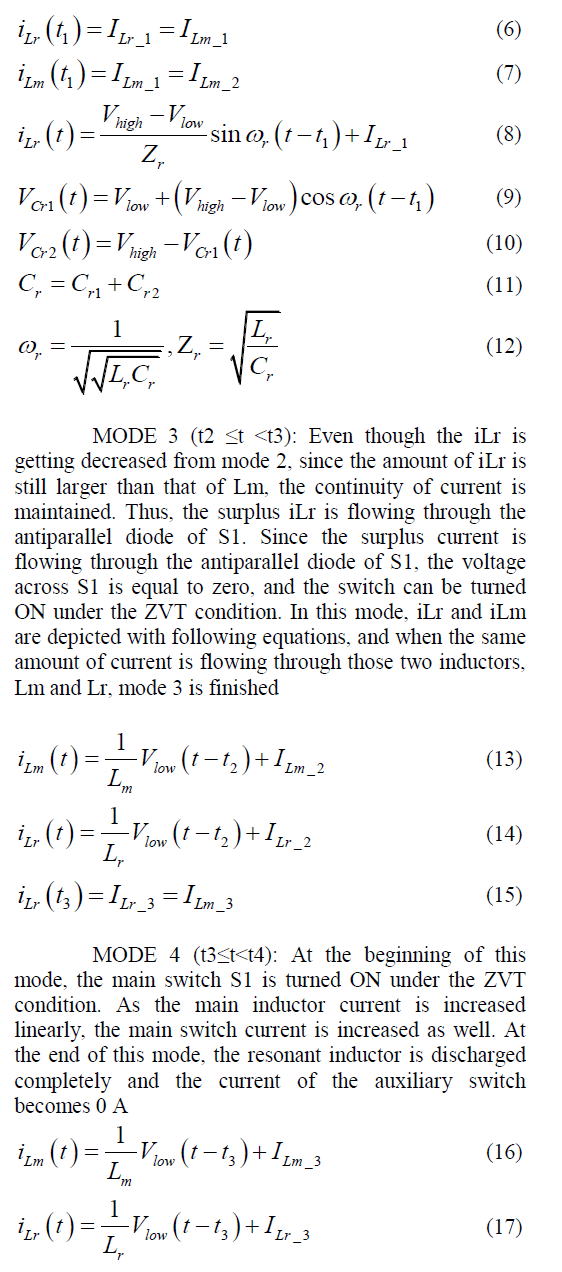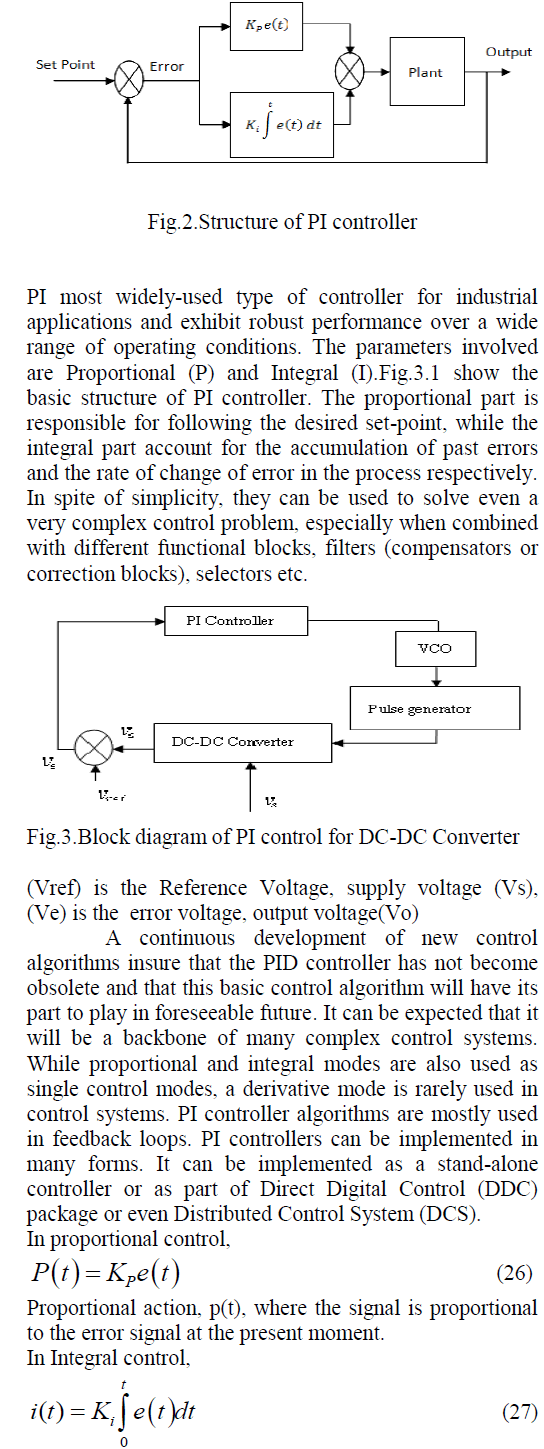
It can be expected that the PIλDμ controller may enhance the systems control performance. One of the most important advantages of the PIλDμ controller is the better control of dynamical systems, which are described by fractional order mathematical models. Another advantage lies in the fact that the PIλDμ controllers are less sensitive to changes of parameters of a controlled system. This is due to the two extra degrees of freedom to better adjust the dynamical properties of a fractional order control system. However, all these claimed benefits were not systematically demonstrated in the literature.

IMPROVED PARTICLE SWARM OPTIMIZATION ALGORITHM

To enhance the refined pinpointing search ability and to strike a balance between exploration and exploitation of available PSOs, the following improvements are proposed

Velocity Updating:

Since the two random parameters r1 and r2 are independently generated, inevitably there are cases in which they are both too large and too small. In the former, both the personal and social experiences accumulated so far are overused and the particle might be driven away from the local optimum. For the latter case, both the personal and social experiences are not fully used, so the particle might not be able to find the local optimum. Therefore, the convergence performance of the algorithm is undermined. In other words, the two random weighting parameters reflecting the experiences of his own and his companions are not completely independent. By modelling this reasoning ability into an updating formula and noting the sum of the two inter-related weighting parameters can be set to 1, one singlerandom parameter that includes the cognitive and social experiences of the particle for updating its velocity is proposed. Therefore, the velocity is updated by using

It should be noted that the communication between different particles in the proposed search procedure is set up in a hierarchical manner rather than a hierarchical manner.

Exceeding Boundary Control:

In updating the position of particles using (32),it is very common to find the coordinates of the new particles lying outside the boundaries of the parameter space. In such cases, the popular approaches used in available PSO algorithms are either to take the boundaries as the coordinates of the new particles, or to keep the coordinates of the particle unchanged but to assign the particle with an extremely poor objective function value. However, either treatment will reduce the diversity of the particles in the searching process and reduce the global search ability of the algorithm correspondingly. Therefore, in the improved PSO algorithm, a different approach is proposed in that if a new particle moves outside the boundaries, the current velocity of the particle in question is modified using

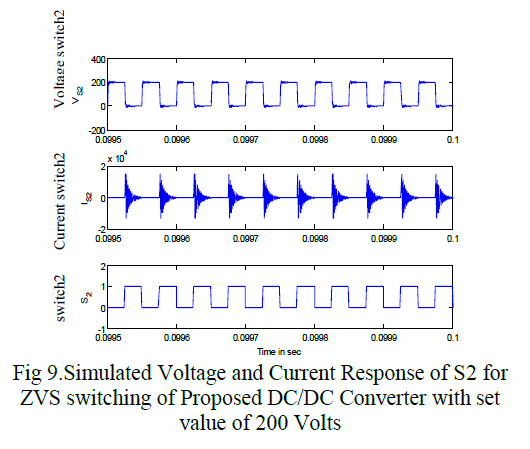CONCLUSION

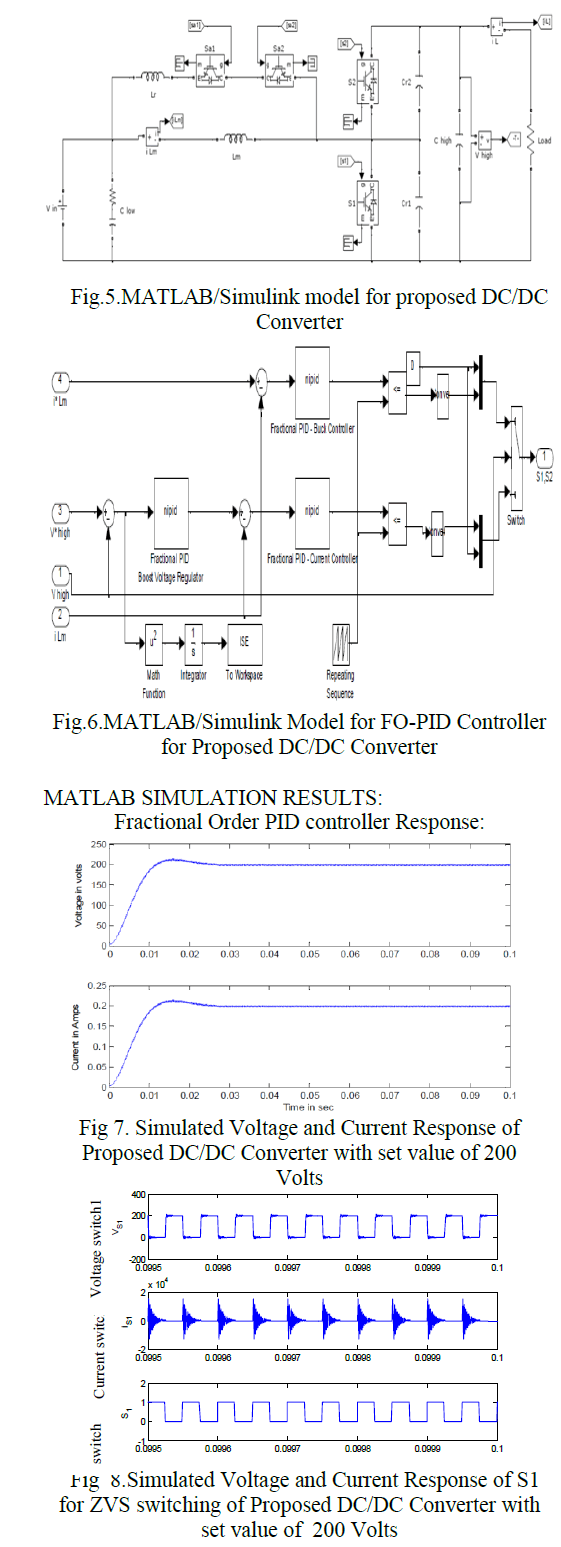
A method for tuning of PI and fractional order PID controller tuning using Artificial intelligence is proposed. The presented method is based determination of Kp , Ki and Kd for the conventional PI Controller. Similarly Kp , Ki, Kd, λ and μ is found by using IPSO. The simulation results that demonstrate that controller has better response compare with the PI and FO-PID controller using tuning of AI techniques from the observation. The PI and FOPID controller is tuned with IPSO. The IPSO based Fractional order PID controller has the best response compared with the performance of the other controllers and tuning method mentioned above.

References

J.G. Zeigler and N.B. Nichols,” Optimum setting for automatic controller’, ASME Trans., pp. 759-768, 1942
S.Manabe, “The non – integer integral and its application to control systems,” ETJ of Japan, vol.6, no.3-4, pp.83-87, 1961.4.
K.J.Astrom, CC.Hang, P.Pearson and W.K Ho:” A self-tuning controller with PID structure.” Inst.J.of Control, 38, pp. 401-417(1983)
K.J.Astrom and T. Haggland;” Automatic tuning of PID controllers”, Instrument Society of America (1988).
G. Maione and P. Lino, “New Tuning Rules for Fractional PIλDμ controllers”, Nonlinear Dynamics, 2006.
M. Zhuang and D P Atherton, “Automatic tunning of Optimum PID controllers,” in IEEE Proceeding- Control theory and Application, vol. 140, 1993, pp.216-224
K.J.Astrom and T. Haggland, “PID Controllers: Theory, Design and Tuning.” Research Triangle Park, NC: International Society for Measurement and Controls, 1995
I.Petras, “The fractional-order controllers: Methods for their synthesis and application”, J.Elect.Eng, vol.50, no.9-10, pp.284-288, 1999.
I.Podlubny, “Fractional-order systems and PIλDμ- CONTROLLERS,” IEEE Trans. Automat. Contr., vol.44, pp.208-214, Jan.1999.
Podlubny,I.: “Fractional – order Systems and fractional order controllers.”Inst.Exp.Phys. Slovak Academy of Science N-1UEF-03-94, Kosice
O. Lequin , M. Gevers, M.Mossberg, E.Bosmans and L. Triest , “ Iterative Feedback tuning of PID parameters : Comprision with classical tuning rules,” Control engineering Practice, vol. 11,2003,pp. 1023-1033.
YangQuan Chen , Ivo Petras and DingyuXue ,” Fractional order Control – A Tutorial” American Control Conference , June 10-12, 2009 , pp. 1397-1411
W. Jifeng, L. Yuankai, “Frequncy domain Analysis and Applications for Fractional Order Control System”, IOP,Journal of Physics:Conf. 13, pp.268- 273, 2005.
K. Bettou, A. Charef, F. Mesquine, “A new design method for fractional PIλDμ controller”, IJ-STA, vol. 2, pp.414-429, 2008.
B. Vinagre, I. Podlubny, L Dorcak and V. Feliu, “On fractional PID controllers: A frequency domain approach”,IFAC workshop on digital control. Past, present and future of PID control, pp. 53–58, Terrasa, Spain, 2000.