ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
1Anant G. Kulkarni, 2Dr. M. F. Qureshi, 3Dr. Manoj Jha
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper presents study of tune Fuzzy based Fault Diagnosis Model of Induction Motor using GA. Interval Type-2 Fuzzy Logic Controller (IT2FLC) where the fuzzy parameters, e.g. Fuzzy Membership Functions and Fuzzy Rule Bases are tuned by Genetic Algorithm (GAs) known as Genetic Interval Type2 Fuzzy System (GIT2FS). The GFS are discussed briefly, later, the proposed design is explained. This is referred as Knowledge Base Tuning using Genetic Algorithm for Interval Type-2 Fuzzy based Fault Diagnosis Model of Induction Motor.
Keywords |
| GA, Interval Type-2 Fuzzy Logic Controller (IT2FLC), Genetic Interval Type2 Fuzzy System (GIT2FS). |
I. INTRODUCTION |
| GA is main evolutionary algorithms for Interval Type-2 Fuzzy System (GIT2FS). GAs is general purpose search algorithms. Mainly there are three technologies, Neural Network (NN), Fuzzy Logic (FL), and Genetic Algorithms (GA) and their hybrid combinations. These thechnologies individually and in combination can be employed to solve problems. The combinations include neuro-fuzzy, GA-fuzzy, neuro-GA, and neuro-fuzzy-GA technologies. It is referred as artificial intelligence (AI), which is an area of computer science concerned with designing intelligent computer systems. It is like human behavior. |
| In the field of soft computing Genetic Algorithms are unorthodox search and optimization algorithms, which mimic some of the processes of natural evolution. GA is evolutionary algorithms under guided random, which is search technique. Engineering, computational science, manufacturing, mathematics, physics, and other fields are application of Genetic Algorithms. GA is based on natural genetic. It provides healthy and strong search capabilities in complex spaces. GA offer a valid approach to effective search process and problem ability efficient. |
| GA is very different from most of the traditional optimization methods. GA need design space to be converted into genetic space. GA works with a coding of variables. The advantage of working with a coding of variable space is that coding discretizes the search space even though the function may be continuous. GA uses a population of points at one time in contrast to the single point approach by traditional optimization methods. It processes a number of designs at the same time. Algorithm is started with a set of solution represented by chromosomes, called populations which develop slowly over time through a process of controlled variation and competition. Solution of one population are taken and used to form a new population. This is motivated by hope that new population will be better than the old one. Solution which are selected to form new population (offspring), are selected according to their fitness and must be planed for each problem to be solved. The more suitable they are, the more chances they have to reproduce. This is repeated until some conditions for improvement of best solution are satisfied. The new population is further evaluated and tested for termination. If the termination criteria are not met, the population is iteratively operated by the three operators and evaluated until the termination criteria are met. One cycle of these operations and the subsequent evaluation procedure is known as a generation in GA terminology. Crossover is a recombination operator. In GA criteria are required to be expressed in terms of an objective function which is usually called to as a fitness function. |
| Fitness is defined as a figure of merit, which is to be either maximized or minimized. The genetic operators are reproduction, crossover, mutation, inversion, dominance, detection, duplication, translocation, segregation, speciation, migration, mating and sharing. Mutation operator when compared to cross over is used sparingly. Some Genetic Algorithm terms are shown in table 5.1. |
 |
| GIT2FS is basically a fuzzy system type-2 augmented by a learning process based on a genetic algorithm (GA). Used to store complex unstructured information and structured used by a computer system is called as knowledge base (KB) technology. In GIT2FS, GAs operates to search an appropriate Knowledge Base (KB) of a fuzzy system for a particular problem. The optimization space is developed by Knowledge Base (KB) parameters. The Knowledge Base (KB) parameter is transformed into suitable genetic representation on which the search process runs. The KB is composed by interval type-2 membership functions (IT2MF), denoted (MF), and fuzzy rule base (RB), as mentioned before. There are some options to design Genetic IT2 Fuzzy System, e.g. tuning or learning membership functions, or fuzzy rule base or both of them, sequentially or concurrently. An individual population represents parameters of the membership function shapes at which fuzzy rule base is predefined in advance and then tuning membership function take place. The population represents all of fuzzy rules possibility that membership functions is assumed before, if be desired to tune fuzzy rules base. Figure 5.1 shows these conceptions. Recently, there are some successful applications of GIT2FS to real world problems, e.g. modeling and decision making, control, robotics, manufacturing, consumer products. |
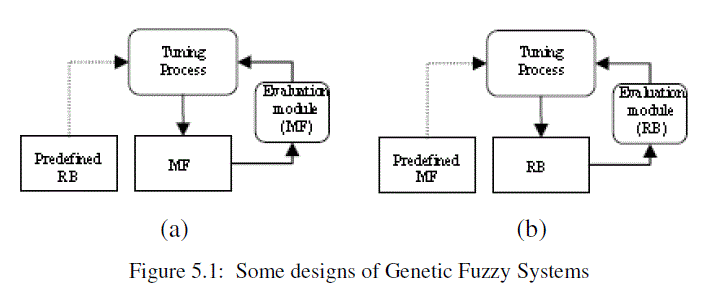 |
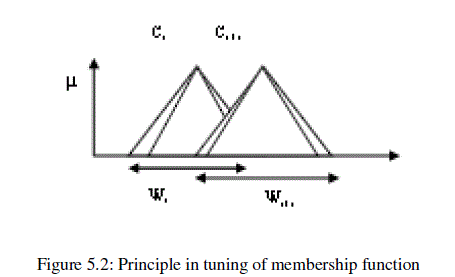
| Further we will describe application a GIT2FS in behavior based mobile robot. Afterwards, a GIT2FS is then applied as a searching algorithm to tune the value of knowledge bases that described in next subsection. Where ki, ji are adjustment coefficient, Cx, and Wx are set of centre and width of each fuzzy membership function. It means ki makes each center of membership function move to the right or left and ji makes them wider or sharper, as shown in figure. 5.2. |
| After that, the adjustment coefficients are encoded to form the population, as presented as below. |
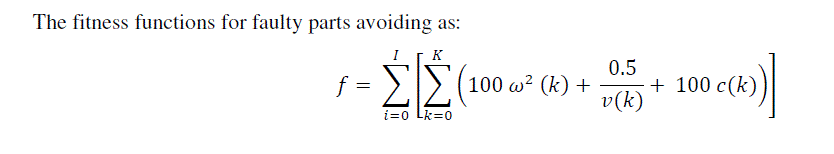 |
 |
| In rule base searching, each of the parameter is encoded into integer codes. Integer codes are based on number of output membership function. The coded parameters are arranged as show in the following equation. This equation is form chromosome of the population, as shown below. |
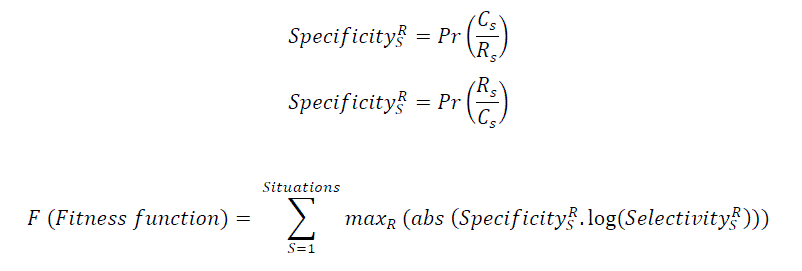 |
| Randomly generated initial populations are first step of GA process. All chromosomes are evaluated and associated base on fitness function. Fitness function associated with linear ranking method to determine the members of the new generation population. |
| The fitness functions for faulty parts avoiding as: |
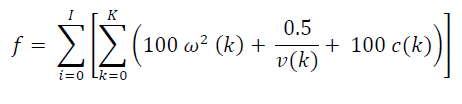 |
| Where I is the total number of start position, K is the number of step simulation for each start position, ω(k), and v(k) are the rotational speed and the faulty speed at k, respectively, and c is constant for health check of IM, 0 if there is no fault and 1 if there is fault. This function is minimized in order to achieve the condition than the motor run by avoiding fault, higher speed, and mostly reliable speed. Recombination, mutation and crossover, are three operators of GA with fixed crossover probability rate (Pc) and probability mutation rate (Pm), that are 0.7, and 0.7 parameter numbers, respectively. The number of new generation is adjusted by Generation Gap constant (GGAP), which is 0.9. The procedure is repeated until the termination condition is reached. It has been presented Interval Type2Fuzzy Logic Controller (IT2FLC) where the fuzzy knowledge based, i.e. membership functions and rule bases, are tuned by Genetic Algorithm (GAs), known as Genetic Fuzzy System (GIT2FS), to generate individual command action. The model is designed in order to detect faults in IM. The best fitness knowledge base is obtained by learning the RB in advance and then tuning the MF after. B |
II RELATED WORK |
| There are a numbers of research work have been done before in order to determine the most automatically and effectively way to identify and classify the fault diagnosis of Induction Motor. H. Guldemir (2003) proposed Detection of airgap eccentricity using line current spectrum of induction motors. Y. Liu (2007) worked on A system of detection, analysis and diagnosis on electro-mechanic systems. Qureshin et. al (2005) contributed his work on the fuzzy based simulation and design of fuzzy logic controller for variable control and position in nuclear control. Tan, W. W. and Pall, S. N. (2003) contributed on Performance study of type-2 fuzzy controllers. S. E. Zouzou, W. Laala, S. Guedidi and M. |
| Sahraoui (2009) presented work on Fuzzy Logic Approach for the Diagnosis of Rotor Faults in Squirrel Cage Induction Motors. Motor Current Signature Analysis (MCSA) was used. The strategy rests on the follow-up (in amplitude and frequency) of the harmonics representing the defects of the broken bars, preparing and thus generating the adequate inputs for the treatment where the decision is made by fuzzy logic. Z. Ye, A. Sadeghian, B. Wu (2006) presented Mechanical fault diagnostics for induction motor with variable speed drives using adaptative neuro-fuzzy inference system. Takagi & Sugeno (1985) studied on the fuzzy identification of systems and its application to modeling and control of engineering systems. Jamshidi (1997) contributed on his work for fuzzy control of complex systems in soft computing methods. Mamdani E.H. (1974, 76) contributed his work on application of fuzzy algorithm for simple dynamic plant and advances in linguistic synthesis of fuzzy controllers. Tong R.M. (1978) reported on synthesis of fuzzy models for industrial process. R. Alcal´a, J. Alcal´a-Fdez, and F. Herrera (2007) introduced a proposal for the genetic lateral tuning of linguistic fuzzy systems and its interaction with rule selection. An innovative study on fault diagnosis of Induction Motor using hybrid FFT and soft computing techniques is proposed in this research work. In the proposed methodology a genetically tuned type-2 FFT fuzzy system and also ANFIS is to be developed. Before using the raw data available from the industrial and commercial sources, it will be normalized for mapping in 0,1 range. This section presented the literature review on different fuzzy techniques, various fault diagnosis of induction motor, fast Fourier transform implementation and fuzzy logic. Review covered variety of topic, methods, techniques and approaches |
III . INTERVAL TYPE-2 FUZZY LOGIC CONTROLLERS |
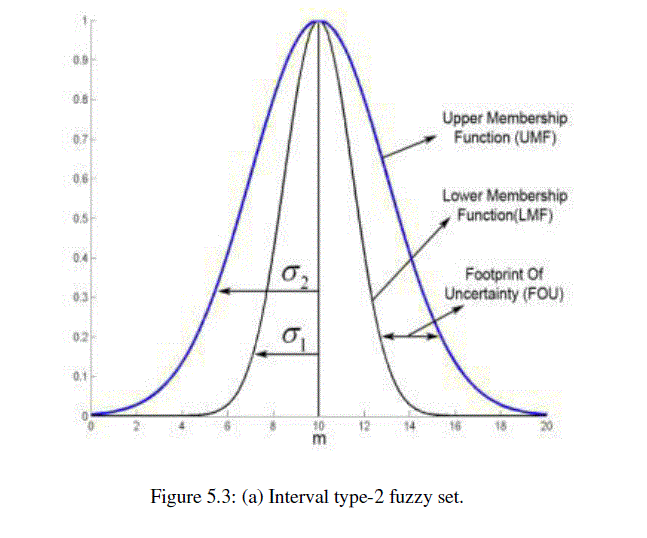
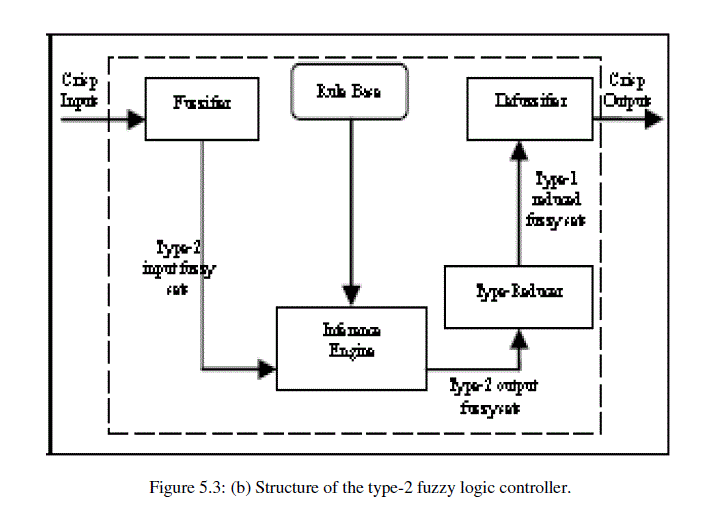
| Limitation of type-1 fuzzy sets is unable to convey the uncertainties about the membership functions and it is two dimensional. Type-2 fuzzy sets are handled more uncertainty. Type-2 fuzzy membership functions are three dimensional. An interval type-2 fuzzy set is shown in figure 5.3(a), which represent the inputs or/and outputs of the fuzzy logic controller. Interval type-2 fuzzy logic controller uses interval type-2 fuzzy sets where all the third dimension values equal to one. Help to simplify the computation is use of interval type-2 FLC. Figure 5.3(b) shows the structure of interval type-2 FLC. Five main components of fuzzy logic controller are Rule Base, Fuzzifier, Inference Engine, Type-Reducer and Defuzzifier. |
 |
 |
| Working of interval type-2 fuzzy logic controller is as follows: |
| First input sensors provide crisp inputs. Fuzzifier converts crisp input into type-2 fuzzy sets. Fuzzifier is used for fuzzification. Fuzzification refers to replacing a crisp set into set with sharply defined boundaries, with a set whose boundaries are fuzzy. Generally there are three types of Fuzzifier; (i) singleton Fuzzifier, (ii) trapezoidal or triangular Fuzzifier and (iii) Gaussian Fuzzifier. Usually used singleton fuzzification in interval type-2 FLC due to simplicity and suitability. Type-2 fuzzy is input of interface engine and it activates the interface engine. Rule base produce output type-2 fuzzy sets. The type-2 FLC rules are same as in a type-1 Fuzzy Logic Controller. But consequents or/and the antecedents will be represented by interval type-2 fuzzy sets. Fired rule combines with the help of interface engine and produce mapping from input type-2 fuzzy sets to output type-2 fuzzy sets. Output of interface engine (output type-2 fuzzy sets) is input of type-reducer which combine output sets and centroid calculation take place, which conduct to type-1 fuzzy sets called the type-reduced sets [Karnik, N.N. et. al, 1998]. Projection of a type-2 fuzzy set into a type-1 fuzzy set and also acts as a measure of uncertainty for that set is possible due to centroid of type-2 fuzzy set. Typereduction in a type-2 fuzzy logic system is an advanced version of the defuzzification operation in a type-1 FLS. There are many types of type-reduction methods such as height, modified height, center-of-sets and centroid [Qilian Liang et. al, 2000]. |
| Center of Sets type-reduction is used in this research. Problem takes place in simple height and modified height typereductions and centroid type-reduction, when only one rule fires. Type reduced sets are defuzzified that means called defuzzification. It convert finite interval of numbers into average of the two end-points of this interval. Finally obtain crisp output. |
IV .THE GENETIC ALGORITHM (GA) BASED EVOLUTIONARY SYSTEM |
| Genetic algorithm and evolutionary strategies mimic the principle of natural genetics and natural selection to construct search and optimization procedures. The Genetic Algorithm chromosome having the interval type-2 membership functions (MFs) parameters. parameters are for inputs and outputs of the induction motor (IM) interval type-2 Fuzzy Logic Controller (FLC). Fuzzy logic controller divided into three stages; Fuzzification, fuzzy interface and defuzzyfication. Here used the interval type-2 fuzzy set. These fuzzy set is described by a Gaussian primary MF with uncertain standard deviation. Figure 5.3 (a) show the interval type-2 fuzzy sets. Chromosome consists genes, encoding to encode real values by GA based system. Thirty chromosomes are in each GA population with elitist selection strategy. Procedure and steps of GA based system is as follows: |
| i) Step i: Thirty chromosomes are generated randomly. He chromosome counter is set to one - first chromosome. The “Generation Counter” is set to 1 – the first generation. |
| ii) Type-2 Fuzzy Logic Controller is constructed using the chromosome “Chromosome Counter” and is executed on 400 control steps to provide a fitness for the chromosome. During fitness evaluation, a healthy condition is in place to avoid the motor fault. After a controller has been executed for 400 control steps, a fixed controller takes over control. |
| iii) If “Chromosome counter” < 30, increment “Chromosome Counter” by one and go to Step ii, Otherwise proceed to Step iv. |
| iv) The chromosome is preserved separately |
| v) If “Generation Counter” = 1 then store current population, copy it to a new population P and proceed to Step 6. |
| vi) Use roulette wheel selection on population P to populate the breeding pool. Else, select 30 best chromosomes from population “Generation Counter” and population “Generation Counter”-1 and create a new population P. |
| vii) Crossover is applied to chromosomes in the breeding pool and “chromosome consistency” is checked (*). |
| viii) “Generation Counter” is incremented. If “Generation Counter” < the number of maximum generations or if the desired performance is not achieved, reset “Chromosome Counter” to 1 and go to Step ii, else go to Step ix. |
| ix) Chromosome with best fitness is kept and solution has been achieved; END. |
| (*) The crossover operator employed computes the arithmetic average between two genes. It is used with a probability of 100% to force. Solution space in between the previously discovered, parental solutions explore by GA. In the IT2FLC correctness of the chromosome’s genes in relation to their function is done with chromosome consistency. |
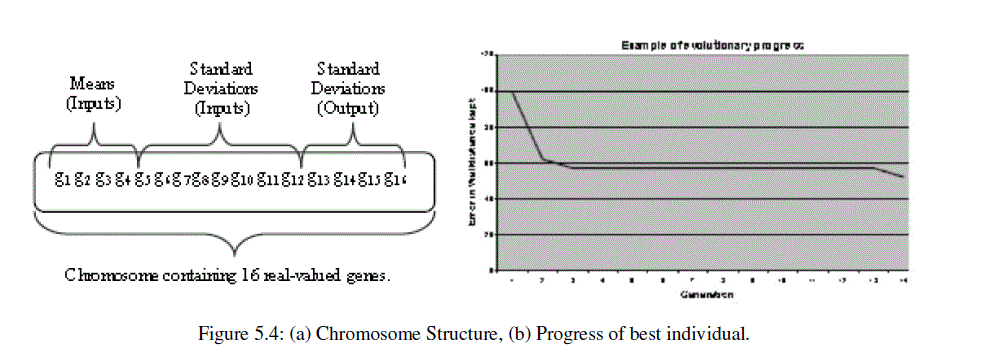 |
| One certain mean and two standard deviations are three parameters. Each input type-2 MF is represented by this parameters. The type-2 FLC inputs are represented by twelve genes. The fuzzy logic controller have two input sensors and each sensors represented by two type-2 membership functions (MFs). Three parameters represent membership function. The type-2 FLC has one output governing the motor health condition of speed. Output type-2 MFs are evolved using only standard deviations. Means are fixed to guarantee that the FLC outputs are within the allowed domain of the outputs. Figure 5.4 (a) shows the GA chromosome having sixteen genes for this type-2 FLC. Sixteen genes mean twelve inputs plus four outputs. |
| The fitness of each chromosome is generated by monitoring, how the generated type-2 FLC has succeeded in following the edge at the desired distance over 400 controls steps. Figure 5.4 (b) shows evolutionary progress. Figure 5.4 (b) shows the performance of the best individual found so far against the number of generations. Performance of the series of three type-1 FLCs with 4, 9 and 25 rules and of the evolved type-2 FLC against a manually designed type-2 FLC have compared. |
| Tuning a modified Mamdani fuzzy rule base system (FRBS) with a GA |
| GAs is useful for tuning the database and the rule-base of FRBS (Maniadakis and Surmann 1999; Cordón et al. 2001). Interval Type2 Fuzzy System GA (IT2FS-GA) for tuning the database in a Mamdani FRBS on the outcomes of a GA which operates on the rule-base (RB-GA) is the impact of this work. Introduces a specific trip scheduling problem which has previously been analyzed with a Mamdani FRBS, this is first work. Then modifications made for this case including the structure of the rules and the database and standard Mamdani FRBS. Finally RB-GA since this is the test bed for the IT2FS –GA. |
| MAMDANI FRBS |
| Figure 5.5 shows the modified Mamdani Fuzzy Rule Based Systems (FRBS) with Selection replacing de-fuzzification, where output is discrete value. The Selection interface takes the fuzzy partition from the Inference system. |
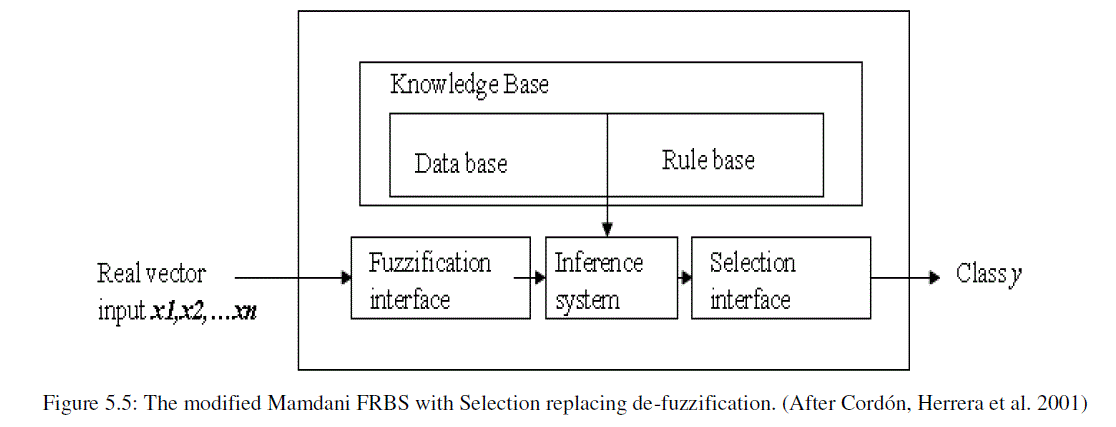 |
| THE RULES GA |
| The chromosome is converted into a rule set of a Mamdani FRBS. Here Genetic Algorithm uses a population of 100 variable length chromosomes. The system is a Pittsburgh GA with a population consisting of individuals encoding rule sets (Cordón et al. 2001; Cordon et al. 2004). |
| The fitness function must be devised for each problem to be solved and is the proportional of test cases. It is correctly classified by a Fuzzy Rule Based Systems (FRBS) using that rule set with an additional weighting factor preferring shorter chromosome lengths. The parameters which represent a potential solution to the problem, genes, are joined together to form a string of values referred to as chromosome. Most conventional GAs codes these chromosomes into binary alphabet. Binary coding has been dispensed with and a real (decimal) coding system adopted. |
| Chromosome Coding the consequent conditions by position and thus storing only their adjectives, there are only (768) different possible antecedent rule sets each with a single consequent (one of 8). Each gene is a pair of integers; the antecedent part and the consequent part. Each individual chromosome consists of a variable length string of up to 100 genes. Crossover is a recombination operator. It is asymmetric single point where a random crossover point is computed for each parent separately and two new strings are composed from the head of one and the tail of the other after duplicate antecedents are deleted. No mutator is allowed to create a chromosome that has duplicate antecedent parts. Thus the two offspring are generally of different lengths. A number of mutation operators are defined. |
| Point Mutation: A randomly selected locus in the antecedent part or the consequent of one gene is incremented or decremented so that it refers to one of the overlapping, neighboring fuzzy-sets. |
| Delete: Delete a sequence of up to a quarter of genes. |
| Extend: extend the chromosome with a random gene. |
| Inversion: a strategy for regrouping genes so that crossover has a chance to test different building blocks. |
| Breeding consists of selection of pairs from the population. Breeding is reproduction using crossover. Mutation is producing new pairs of offspring. |
| Selection is elitist, using a form of ranking selection. Individuals are first ranked by fitness. Then it is working from fittest to least fit, individuals mate with selected members of the old population, offspring replacing least fit individuals. The majority of the populations are subjected to a bout of mutation using a random selection of mutation operators. One feature of ranking selection is that all objective functions which are monotonic on each other are equivalent in effect. |
| Fitness and objective function |
| Assess how well the partitioning of the fuzzy sets also partitions the data is aim of fitness function. There are four axes. Each axes with a number of partitions which thus forms a partitioned hyper-space with multiple “hyper-regions” and all of the classified situations with a particular class to fall within one hyper-region. In this case just eight hyper-regions would be filled. Just eight rules would suffice to classify the data fully and each layer with a single class and represented within a hyper-region. Region for that class can be assigned by specificity (of a situation S in region R and having class C is the probability of S being of class C given having non-zero membership of the region R) and selectivity (situation S in region R and having class C is the probability of S having non-zero membership of region R given class C). Non-zero degree of membership within more than one region is S. For computation fitness; |
| i) Compute the specificity of S multiplied by log of selectivity of S within each of the regions for which it has a degree of membership. |
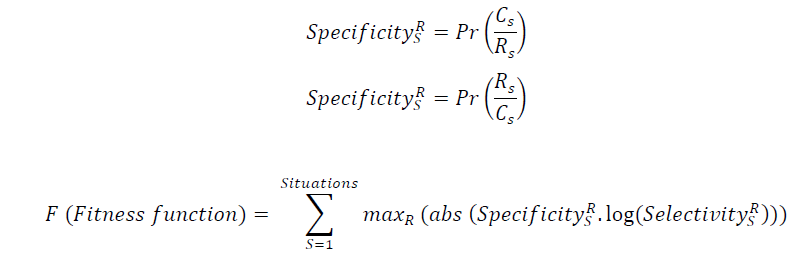 |
V. RESULTS AND DISCUSSION |
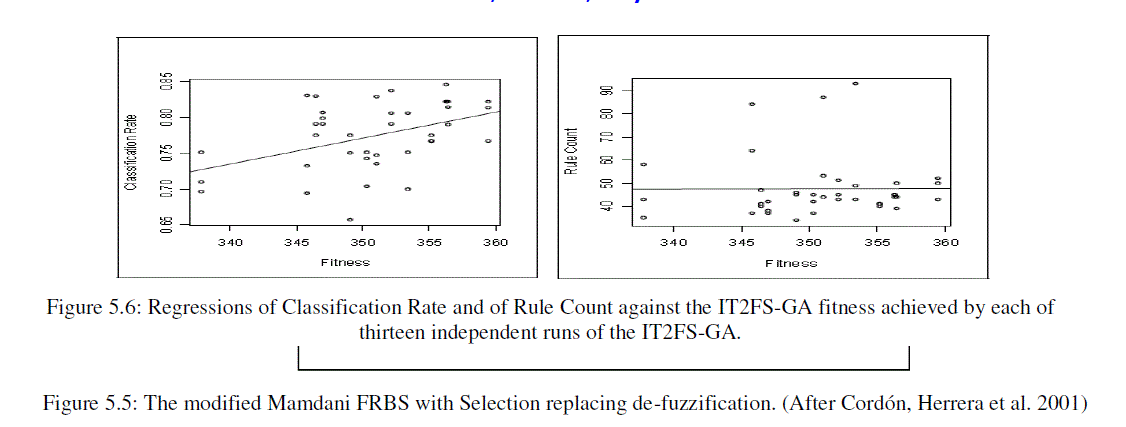
| The Interval Type-2 Fuzzy System Genetic Algorithm (IT2FS-GA) was run 13 times for 100 generations. The elite from each run was preserved. Value of its associated objective function was recorded. Different values of fuzzy sets created. This presented a test of fuzzy-sets. Using each of the acquired fuzzy sets in turn the Rule Base-GA was then run against the full travel decisions data set. Rule Base Genetic Algorithm sprinted with single-best composition. The RB-GA was halted at 10,000 generations. 39 results obtained, when process was repeated in triplicate. Each result provided rule sets; rule count, classification rate and associated value for the objective function assigned to the interval type2 fuzzy-set by the IT2FS-GA. Grouping the three runs. Linear regression of the interval type2 fuzzy-set fitness performed. Classification rate and rule counts obtained. Figure 5.6 shows Regressions of Classification Rate and of Rule Count against the IT2FS-GA fitness achieved by each of thirteen independent runs of the IT2FS-GA. This represented that there is a significant positive trend for the classification rates and no trend for the rule counts. |
 |
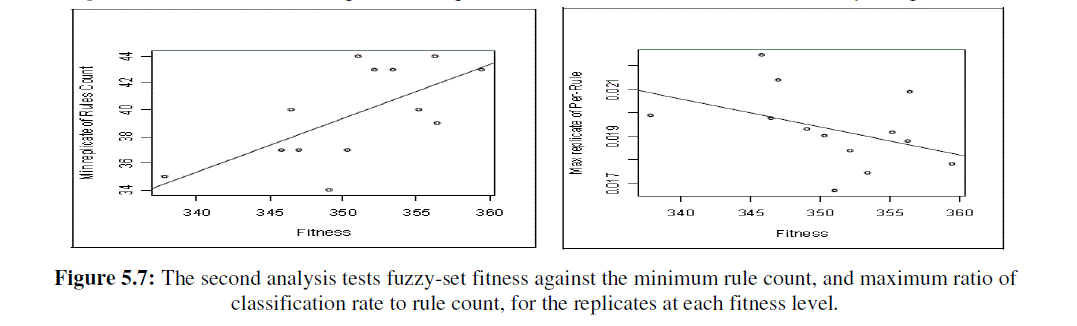
| There is considerable variance and classification rate shows a significant trend. Fitness and rule counts are not independent. The RB-GA optimizes for high classification rates and only reduces rule counts within classification rate. Figure 5.7 shows second analysis tests fuzzy-set fitness against the minimum rule count, and maximum ratio of classification rate to rule count, for the replicates at each fitness level. There is a non-significant positive trend between the smallest per-replicate size of the rule set obtained and IT2FS-GA objective function value. This indicating that the GA may have proceeded faster and all runs of the RB-GA halted after the same number of generations. There is a more significant negative trend with the maximum per-replicate ratio of classification rate to rule count. These indicating that less compact rule sets obtained running with the higher values of the IT2FS-GA fitness, are likely less generalized. |
 |
VI. CONCLUSION |
| Here, for fault analysis of induction motor the GA based architecture to the type-2 MFs of interval type-2 FLCs has been introduced. The performance comparison between type -1 MFs and type-2 FLCs has been shown, and it is found that the type- 2 promising great performance than type -1 MFs .these process will allow to overcome the limitation of model based specifying pseudo-optimal MFs for type-2 FLCs .The entropy like measure served as a useful heuristic objective function for the purpose of pre-tuning the database of the FRBS in this problem. There is a positive relationship between the fitness of the fuzzy-sets and the classification success of the RB-GA. |
| There is a suggestion that the rule counts increase with fitness, and there is evidence that classification rate per rulef decreases. |
| The FRBS tuning tackling the larger amount of error related to dimensions as fallows. The selection of axes, |
| a) The number and form of fuzzy-sets on the axes, these points relating to the database; |
| b) The grammar of the rules, and |
| c) The selection of the rules in the rule base. |
| The related work shows the signific. This work shows some significant benefits to pre-tuning by a simple heuristic. The GAs in general executes a robust search than pure hill-climbing. The decoding scheme in the IT2FS-GA limits the shapes of the fuzzy sets and again simplifies the error landscape. The primary execution of RB-GA shows several important things. The GA was stop after a respective set number of runs, and it causes the error in measurement. The performance measures of the IT2FS-GA, which are the same measures, thus are subject to high variance. |