ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
S.Karthik, T.Prabaharan
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper a hybrid genetic and harmony search algorithm is proposed to find the possible best sequence of operation solutions for hybrid flow shop scheduling problems. In this work the problem is considered with respect to the objective of minimization of makespan. Hybrid flow shop scheduling problem is considered for the sequencing of jobs in a hybrid flow shop with two or more identical machines. At first manual calculation has been carried out for the data collected from literature, by using Gantt chart calculation method with random sequences. Further calculations are carried out for multi machine- multi job in batch size, successively by using genetic and harmony search algorithms. Genetic Algorithms performs a global search with the aim of finding the best alternative with respect to the given criteria of goodness and a local search is improved in this work by using the harmony search algorithm
Keywords |
| hybrid flowshop, genetic algorithm, harmony search algorithm, makespan, optimization |
INTRODUCTION |
| Hybrid Flow Shops (HFS) is manufacturing environments that can be found in many real-world situations. The Hybrid Flow Shop consists of a multistage, where each stage is composed of M parallel machines. Each machine is able to process one job at a time. A multistage flowshop is considered to be a hybrid flowshop if one stage at least is made up of more than one machine. Those operations have to be realized sequentially, without overlapping between stages. Job preemption and job splitting are not allowed. Each job has a given processing time at each stage. |
| Ching-I Yang and Jyh-Horng [1],consider a flowshop scheduling problem in the objective to minimize the makespan and also the Search performance is improved in this paper by using Taguchi-based crossover to avoid scheduling conflicts, and dynamic weights which are randomly selected by a fuzzy inference system. |
| Hany Seidgar et al [2], presents a paper on two stages Hybrid Flow Shop in objective is to minimize the weighted sum of completion time and maximum tardiness by using metaheuristic algorithms can be utilized to obtain high quality solutions in a reasonable amount of time. |
| .Hang-Min Cho and Suk-Joo Bae [3], have presented a study on Bi-objective scheduling for re-entrant hybrid flow shop using Pareto genetic algorithm. Local-search based Pareto genetic algorithms based crossover operator is proposed to approximate the Pareto optimal solutions for the minimization of makespan and total tardiness in a re-entrant hybrid flowshop. Gupta et al [4] developed a heuristics algorithm for a two stage hybrid flow shop scheduling to minimize the makespan and total manufacturing time. |
| In Shahsavari Pour and Abolhasani Ashkezari [5], a Bi- Objective Permutation Flow Shop problem is solved by using Genetic Algorithm Coupled with Tabu Search. And the performance of this algorithm is evaluated by performing the experiments, it is coded in VBA. |
| In Abir Ben Hmida and Mohamed haouari [6], a discrepancybased search method is introduce to solve two-stage hybrid flowshop scheduling problems to minimizes the makespan in manufacturing. |
| In Prithwish Chakra borty and Ajith Abraham [7] ,an attempt has been made to improve the search performance of Harmony search by hybridizing it with Differential Evolution algorithm and presented an improved variant of the classical Harmony Search metaheuristic by combined it with a difference vector-based mutation operator borrowed from the DE family of algorithms And the performance of these resulting hybrid algorithm has been compared with classical HS, the global best HS, and a very popular variant of DE. Cengiz kahraman and Mustafa kerim yilmaz [8], has proposed a paper on an application of effective genetic algorithms for solving hybrid flow shop scheduling problems to minimize the makespan value. |
| Le Liu and Hong Zhou [9], have presented a paper on Hybridization of harmony search with variable neighbourhood search for restrictive single-machine earliness/tardiness problem. Several problem-dependent mechanisms are also introduced to improve the search process. In Choong and phon-amnuaisuk [10], hybrid heuristic algorithms that combine global and local search by using evolutionary algorithm to perform exploration to minimize makespan in hybrid flow shop scheduling. |
PROBLEM DESCRIPTION |
| A. Flow shop problem |
| Flow shop scheduling is the common problem to solve with the modern heuristic and Meta heuristic techniques in the literature.in an n job, m machine flow shop, each of n jobs is to be processed on a set of m machines. The order of the machine is fixed. The processing time of each job on each machine is assumed to be known. A machine processes one job at a time and job is processed on one machine at a time with or without pre-emption. Flow shop problems are solve to find the job sequences by considering the objectives such as minimization of maximum make span, total tardiness, total weight tardiness, earliness/lateness, and etc. |
| B. Hybrid flow shop problem |
| The problem going to be resolve in this project is hybrid flow shop problem. Hybrid flow shop scheduling problem is applied for the sequencing of jobs in a hybrid flow shop with two or more identical machines. This type of manufacturing systems is relatively common in all area of manufacturing. |
| Based on hybrid flow shop problem, brake dust cover manufacturing data from the literature [11] is considered. The process of brake dust cover begins from pre forming and ends with finishing the brake dust cover. A brake dust cover manufacturing process is illustrated in Fig [1] which is of a leading brake dust cover manufacturing company located in Hosur, Tamilnadu. The present study models the case study problem consist eight stages with two or more identical machines in each stages. |
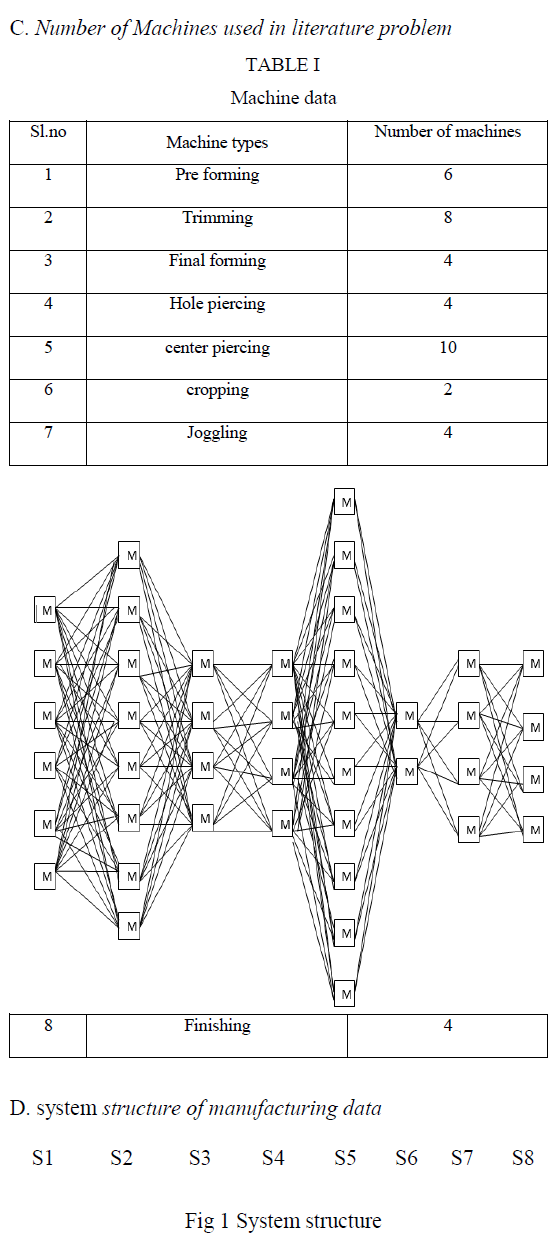 |
| The following structure shows the possible ways of sequencing the jobs. For example the first job can go any one of the six machines in stage1 [S1] irrespective of orders. Similarly the remaining process also it would be like that. The following fig [2] shows it clearly. |
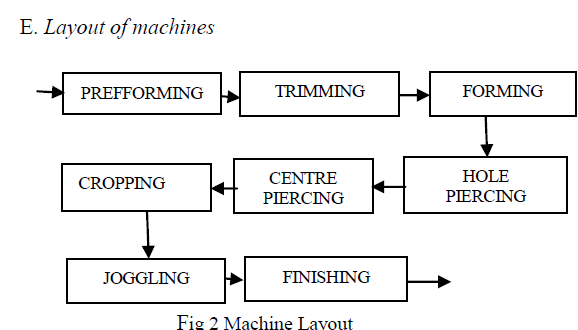 |
DESCRIPTION OF PROPOSED APPROACH |
| A. Genetic Algorithm |
| Genetic Algorithms (GA) are adaptive heuristic search algorithm based on the evolutionary ideas of natural selection and genetic, which mimic some of the processes of natural evolution these criteria are required to be stated in terms of an objective function which are usually referred to as a fitness function. Fitness is defined as a figure of merit, which is to be either maximized or minimized. It is further required that the alternatives be coded in some specific finite length which consists of symbols from some finite alphabet. These strings are called chromosomes and the symbols that form the chromosomes are known as genes |
| Binary alphabet (0, 1) – binary strings |
| Real alphabet (0-9) – decimal strings |
| Starting with an initial population of chromosomes, one or more of the genetic inheritance operators are applied to generate offspring that competes for survival to make up the next generation of population. The genetic inheritance operators are reproduction, cross over, mutation, inversion, dominance, deletion, duplication, translocation, segregation, speciation, migration, sharing and mating. Mostly we used the application as such, reproduction, cross over and mutation. Need for mutation is to keep the variety of the population. Three most important aspects of using GA |
| Definition of objective function |
| Definition and implementation of genetic representation. |
| Definition and implementation of genetic operators. |
| B. Harmony Search algorithm |
| Harmony Search Algorithm is based on the musical process of searching for the perfect state of harmony.. HSA is inspired from the artificial phenomenon of creating sounds, imitating musicians’ behaviour. Just as the musicians try to improve their music (based on aesthetic and acoustic criteria), the algorithm seeks for certain values that optimize the objective function and at the same time satisfy the problem’s constraints. And in the same way a music band improves rehearsal after rehearsal, HSA improves iteration after iteration. After the first successful applications of the new method, it was obvious that HS Algorithm is a powerful and efficient tool, with the extra advantage of having a simple structure. This advantage allows the combination of HSA with other algorithms. It does not require initial value settings of the decision variables, it imposes fewer mathematical requirements and as a stochastic algorithm, it doesn’t require derivative information. Compared to existing algorithms, HSA can be successfully applied using decimal numbers and doesn’t require their conversions to binary system. Programming HSA applications is simple and the code is usually shorter and runs faster. The fact that Harmony Search Algorithm creates a new vector from all the existing vectors is an extra advantage. On the contrary, Genetic Algorithm, maybe the most popular optimization technique, creates the new vector only from the two parents. |
| C. Hybrid Algorithm |
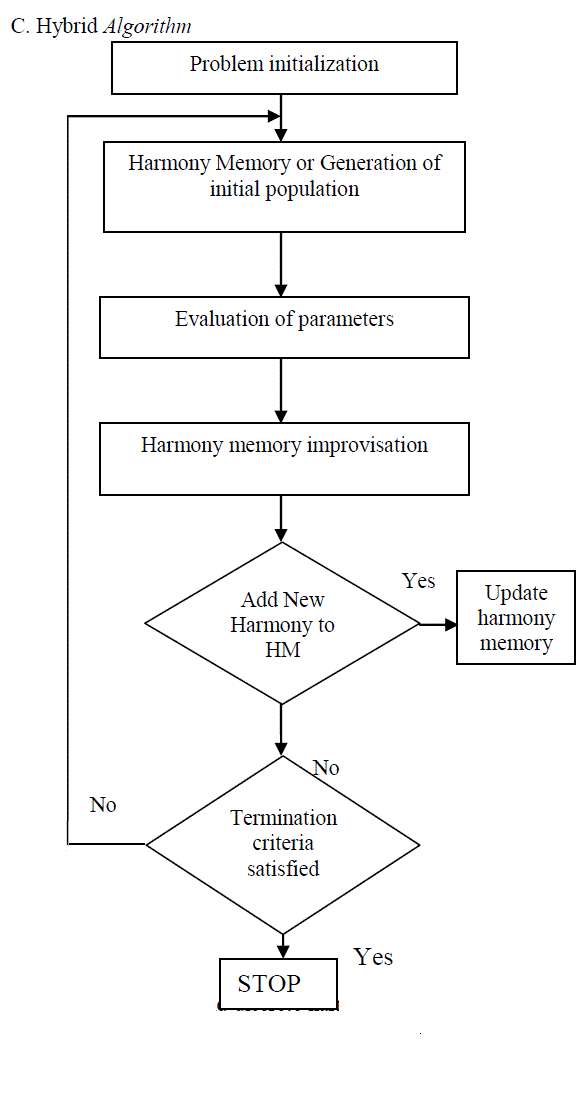 |
| Fig 3 Flowchart for hybrid algorithm |
| In this work genetic and discrete harmony search algorithm is combined to find the best sequence of operation. The hybrid genetic and harmony search algorithms consist of six steps |
| Step 1: Problem initialization |
| During this stage identify the objective function and set the harmony memory size [HMS], harmony memory considering rate [HMCR], pitch adjusting rate [PAR], number of iteration [NI]. |
| Step 2: Generation of initial population or harmony memory Choose the initial value of xi from X1 parameters |
 |
| Evaluate the fitness f[x] in each chromosome x in the population and also find the average makespan of the each population in the harmony memory. |
| Step 4: Harmony memory improvisation |
| Improvisation can be carried out in two stages by using PAR and HMCR.The HMCR Parameter is the probability of selecting one value of the decision variable. For example, if (HMCR =0.90), that indicates that the probability of selecting the value of decision variable from historic value in the HM with the probability is 90%, and the value of decision variable is selected from its Possible range with a probability of 10%.HMCR value will be lies between 0.5 to 0.9. Pitch adjustment makes a sequence of local changes (pitch adjustments) on the new harmony with probability PAR where (0≤PAR≤1) the values of decision variables not obtained by memory consideration with probability of (1− PAR) are not changed. For example, if HMCR=90% and PAR=20%, the probability of selecting the neighbouring value of any decision variable is 18%.PAR value will lies between 0.3 to 0.5. |
| Step 5: Update harmony memory |
| If the New Harmony vector has a better objective function value than the worst harmony stored in the HM, then it is included in the HM and the worst harmony vector is excluded from the HM. |
NUMERICAL ILLUSTRATION FOR HYBRID GENETIC AND HARMONY SEARCH ALGORITHM |
| Problem will be taken from the journal [11] |
| Step: 1 Problem Initialization |
| Objective is to reduce makespan in manufacturing. |
| HMCR = 0.9 |
| PAR = 0.4 |
| NI = 1 |
| HMS = 6 |
| Step: 2 Generation of Initial Population (or) Harmony Memory |
| Generate random population of n chromosomes (suitable solutions for problem) as shown in the following table |
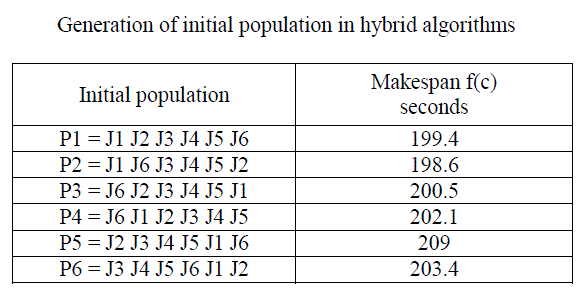 |
| TABLE 2 |
| Step 3: Evaluation of parameters for generated initial population |
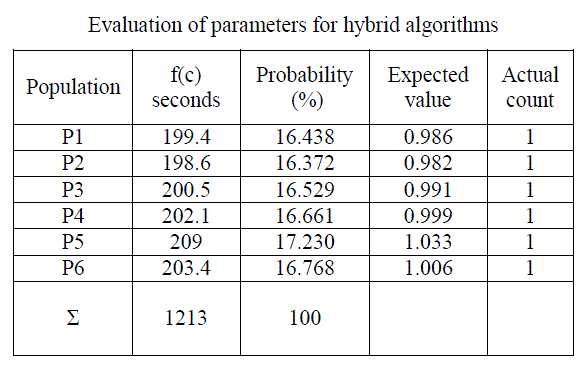 |
| Table: 3 |
 |
 |
 |
CONCLUSION |
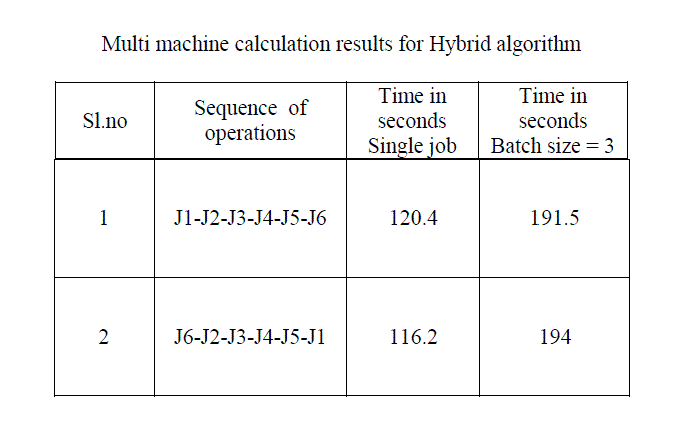
| Genetic-Harmony search algorithm searches larger regions of the solution space effectively using both harmony search algorithm based local search feature with genetic algorithm based global search capability. Genetic-harmony search algorithm was applied to literature data and compared it with manual calculation result. |
| Hybrid algorithms are usually better than genetic algorithms, when it comes to problems that have numerous locally optimum solutions. |
| Hybrid Algorithm could be able to found the better makespan time for hybrid flowshop scheduling problem, but still we may refine the result further by increasing more number of iterations and also by changing the hybridizing procedure. |
ACKNOWLEDGEMENTS |
| The authors would like to thank the department of mechanical engineering, Mepco Schlenk engineering college Sivakasi, for carrying out this project work. |
References |
|