Identifying Quadratic Residuity Using Legendre-Jacobi Symbol

Abstract

Cryptography is the study of “Mathematical Systems” involving two kinds of security protocols: Privacy and Authentication. The mathematical concepts from the branch of number theory known as Modular arithmetic, Quadratic residue are significantly useful in cryptography. Cryptography Deals with large number integers i.e. integers as big as hundred digits and more. In such situation identifying whether an integer “a” is quadratic residue modulo “p” where p is Prime can be achieved using Legendre and Jacobi Symbol. This paper introduces to the mathematical concepts of Quadratic Residue, Fermat's little theorem, Euler’s criterion and Legendre and Jacobi symbol. However it has been observed that Jacobi symbol in case of some example fails to give correct result and therefore the Limitation for predicting the quadratic residue.

Keywords

Cryptography, Quadratic residue, Legendre Jacobi symbol

INTRODUCTION

Cryptography is the study of exchange of information between sender and receiver over an insecure channel is such a way that the opponent (any third user) cannot understand what is being said [2][13][18].The actual information sender wants to send is called as “Plaintext”, sender converts this plaintext in “Cipher text” (by using different techniques) by applying Key to it. This cipher text is very difficult to read, need mathematical knowledge to read it. At receiver this cipher text gets converted into plaintext by applying key (same or different) to it, so receiver can read it. The conversion from plaintext to cipher text is called encryption and from cipher text to plaintext is called as decryption[13][20].

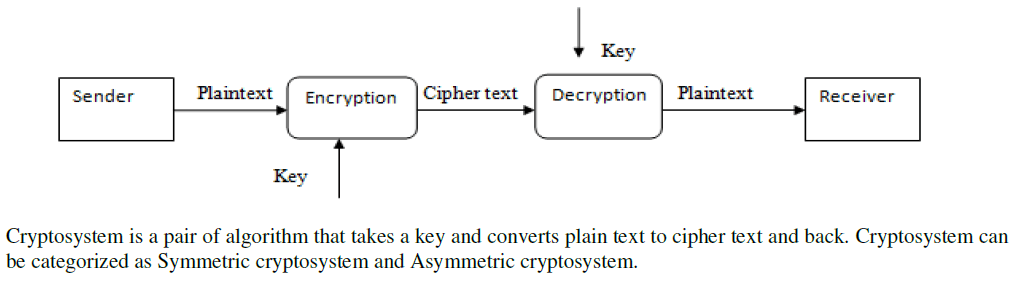Symmetric cryptosystem uses a shared secret key in the encryption process as well as in decryption process .for example DES (Data Encryption Standard)[12][13][18][20], AES(Advance Encryption Standard) [8][18][20],Blowfish[1]. It has few limitations such as key distribution, compromised KDC (Key Distribution Center), random number generation, placement of encryption function.

Asymmetric cryptosystem uses public key for encryption and a private key for decryption, there is no need for a shared secrete [3][20]. Examples of this are Diffie-Hellman [14], RSA [7][12] and Elgamal [5].

All of the techniques used here are based on mathematical concepts of number theory and discrete logarithms. Particularly in number theory most important is integer factorization, modular arithmetic’s. This paper introduces to the mathematical concepts of Quadratic residue, Fermat's little theorem, Euler’s criterion and Legendre and Jacobi symbol. However it has been observed that Jacobi Symbol in case of some example fails to give correct result and therefore the limitation for predicting the quadratic residue.

FERMAT'S LITTLE THEOREM.

Fermat’s little theorem works in two forms. First form is applicable to all but second form has limitation.

Form 1:-

QUADRATIC RESIDUE:

Let a ∈ N and p be an odd prime number such that gcd(p,a) = 1. Then a called a quadratic residue modulo p if a is a perfect square modulo p[4][6][9][13][15][16] i.e. there is a number y such that,

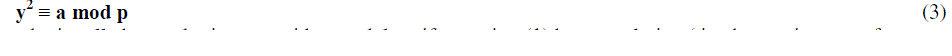So, we find square of all the numbers in z5 set and find each square modulo 5,here we find that there is no such perfect square exist. Here a=2 and p=5 and we conclude that a is quadratic non residue modulo p.

Finding whether a is quadratic residue modulo p becomes a tedious task for large integers. It is therefore necessary that we first identify whether there exists such y which satisfies y2 = a mod p

This can be achieved through Legendre and Jacobi symbol. However, we need to first understand Euler’s criterion as discussed in next section.

EULER’S CRITERION

LEGENDRE SYMBOL.

JACOBI SYMBOL.

It is generalization of Legendre symbol [6][10][11][13].suppose n is and odd positive integer , and the prime power factorization of n is ,

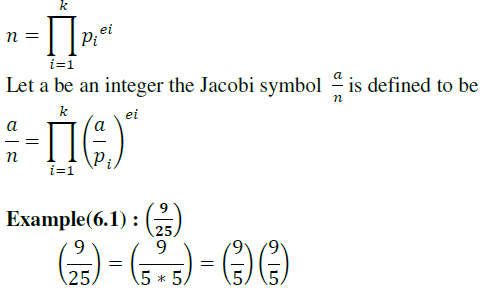CONCLUSION

Cryptography has been built over the mathematical concept to construct hard problems to increase the efficiency of cryptographic algorithms. Quadratic residue is one such important concept used in cryptography. In this paper we have demonstrated how we can identify where an integer a is quadratic residue modulo p (p is prime) using Legendre and Jacobi symbol. Also with the help of example we have shown our observation that the results of Legendre Jacobi Symbol in some cases do not agree with the actual expected results of quadratic residuity.

References

1. Bruce Schneier,”The Blowfish Encryption Algorithm”, Dr. Dobb’s Journal of Software Tools, pp. 4, 38, 40, 98, 99, 1994.
2. Chitra Desai,” A Novel Approach for Digital Signature Scheme Based on Solving Two Hard Problems” IJCMSA: Vol. 6, No. 3-4, July- December 2012, pp. 95– 100.
3. Chitra Desai, Manisha Patil, and Bharti Gawali,”Review of Digital Signature Schemes, International Journal of Mathematics”, Computer Sciences and Information Technology, ISSN: 0974-5580 , Vol. 3, No. 2, pp. 387-402, (July-December 2010).
4. Chris Monico, Michele Elia,” Note on an Additive Characterization of Quadratic Residues Modulo p”, January 27, 2006.
5. ElGamal, T,” A Public Key Cryptosystem and A Signature Scheme Based on Discrete Logarithm”, IEEE Transaction Information Theory IT, 31: 469-472, 1985 http://dsns.csie.nctu.edu.tw/research/crypto/HTML/PDF/C84/10.PDF .
6. Gauss, Carl Friedrich; Clarke, Arthur A. (translator into English) (1986), “Disquisitiones Arithmeticae” (Second, corrected edition), New York: Springer, ISBN 0-387-96254-9.
7. James Robinson, Fermat’s Little Theorem,”Elaboration On History Of Fremat’s Theorem And Implications Of Euler’s Generalization By Means Of The Totient Theorem”, copyright © James Robinson.
8. Joan Daemen and Vincent Rijmen,” Rijndael for AES”., AES Candidate Conference, pp. 343–348, 2000.
9. Lindsay N. Childs "A Concrete Introduction to Higher Algebra", ISBN: 978-0-387-98999-0 (Print) 978-1-4419-8702-0 (Online).
10. Menezes, Alfred J; van Oorschot, Paul C.; Vanstone, Scott A. (2001),"Handbook of AppliedCryptography",[Online] Available: http://www.cacr.math.uwaterloo.ca/hac/about/chap2.pdf.
11. R. Crandall, C. Pomerance.”Prime Numbers, A Computational Perspective”, New York: Springer, 2001
12. Rivest, R., A. Shamir and L. Adleman,“A Method for Obtaining Digital Signature and Publickey Cryptosystem Communications”ACM. 21: 120-126. 1978 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.40.5588.
13. Stinson, Douglas Robert (2006),"Cryptography: Theory and Practice (3rd ed.)", London: CRC Press.
14. Whitfield Diffie and Martin E. Hellman,”New Directions in Cryptography”, IEEE Transactions on Information Theory, 22(6):644-654, 1976.
15. ftp://ftp.disi.unige.it/person/MoraF/MaterialeCTC/Quadratic.pdf
16. en.wikipedia.org/wiki/Quadratic residue.
17. David Angell(10/2012)” Evaluation of Certain Legendre Symbols”, publishes by MAA (http://www.jstor.org/stable/10.4169/amer.math.monthly.119.08.690).
18. G. JULIUS CAESAR and JOHN F. KENNEDY ,” Cryptography”. Security Engineering: A Guide to Building Dependable Distributed Systems.
19. Ken Bogart, Scot Drysdale and Cliff Stein ” Discrete Math for Computer Science Students”.(http://www.cse.iitd.ernet.in/~bagchi/courses/discrete-book/fullbook.pdf)
20. William Stallings , “Cryptography And Network Security: Principles And Practices, 4Th Ed.”.