Implementation of Segmentation and Classification Techniques for Mammogram Images

Neeta V. Jog; S.R.Mahadik

Implementation of Segmentation and Classification Techniques for Mammogram Images

Neeta V. Jog ¹, S.R.Mahadik ²

Lecturer, Medical Electronics, G.P.Miraj, Miraj, Maharashtra, India
Professor, Electronics and Communication, Dr. J.J.Magum College of Engg, Jaysingpur, Maharashtra, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Mammography is an important research field. Mammography Image classification is an area of interest to most of the researchers today. The aim of this paper is to detect the Mammography image for its malignancy. Different methods can be used to detect the malignancy. This paper represents GLDM and Gabor feature extraction methods along with SVM and K-NN classifiers. Experiments were conducted on MIAS database. The results show that combination of GLDM feature extractor with SVM classifier is found to give appropriate results.

Keywords

Mammography; image classification; GLDM; Gabor; SVM; K-NN

INTRODUCTION

Cancer is uncontrolled growth of cells. Breast cancer is the uncontrolled growth of cells in the breast region. Breast cancer is the second leading cause of cancer deaths in women today. Early detection of the cancer can reduce mortality rate. Mammography has reported cancer detection rate of 70-90% which means 10-30% of breast cancers are missed with mammography [1].Early detection of breast cancer can be achieved using Digital Mammography, typically through detection of Characteristics masses and/or micro calcifications .A mammogram is an x-ray of the breast tissue which is designed to identify abnormalities. Studies have shown that radiologists can miss the detection of a significant proportion of abnormalities in addition to having high rates of false positives. Therefore, it would be valuable to develop a computer aided method for mass/tumour classification based on extracted features from the Region of Interest (ROI) in mammograms [3]. Pattern recognition in image processing requires the extraction of features from regions of the image, and the processing of these features with a pattern recognition algorithm. Features are nothing but observable patterns in the image which gives some information about image. For every pattern classification problem, the most important stage is Feature Extraction. The accuracy of the classification depends on the Feature Extraction stage. The motto behind computer aided analysis is not to replace the Radiologists but to have a second opinion and thus provide an efficient support in decision making process of the radiologist. Much research has been done in mammography towards detecting one or more abnormal structures: circumscribed masses [5], speculated lesions [6] and micro-calcifications [4].Other researchers have focused on classifying the breast lesions as benign or malignant. There are different feature descriptors such as GLDM, (Gray Level Difference Method), LBP (Local Binary Patterns), GLRLM(Grey level Run Length Method),Harralick, Gabor texture features and there are classification methods such as SVM,C4.5,K-NN Classifier.

In this paper we have used a GLDM and Gabor feature extraction method over set of mammography images and then tested their performance on SVM and K-NN classification algorithms. The paper is organised as follows with section 2 gives related work.Section3gives explanation about the pre-processing stage where as section 4 describes the feature extraction methods which are used in the experiment. Section 5 comes up with the overview of classification methods. Section 6 provides brief discussion of results. Section 7 gives conclusion derived from this work.

RELATED WORK

Our main aim was binary classification of the mammogram images. A Mammogram image is taken as an input and preprocessing is carried out. The required features are extracted from images. Classification algorithms are applied to the features which will give the result as to whether the image is benign or malignant.

For the experiment we used the MIAS database.(The Mammographic Image Analysis Society digital mammogram database).It is a collection of 78 images. These 78 images contain anomaly. The set of 50 images are used at random from the above set of 78 images. And a set of 25 malignant images are used for testing. We implemented all feature extraction methods which we use in the experiment, in Matlab verion7.1.

Here the image is taken from the database it is preprocessed if required and feature extraction method is used to extract the relevant features from the image and the information is stored in feature extracted database. This information and the ground truth database information regarding the images is given to training block which are the machine learning algorithms where in a trained model is developed. Further the test image and the trained model information is compared and the test image is classified to the appropriate class.ie benign or malignant and finally performance of the classifier is calculated.

PRE-PROCESSING

Pre-processing stage is a step used to increase image quality of Mammograms as they are very difficult to interpret .An histogram equalization can be used to adjust the image contrast so that anomalies can be better emphasized.

FEATURE EXTRACTION

Feature extraction involves simplifying the amount of resources required to describe a large set of data accurately. In image processing, a different set of features can be used to extract the visual information from a given image. Because digital mammography images are specific, not all visual features can be used to correctly describe the relevant image patch. All classes of suspected tissue are different by their shape and tissue composition. This is why the most suitable visual feature descriptors for this kind of images are based on shape and texture. We can use different feature extraction methods and test them on variety of classifiers. We are using GLDM feature descriptor.

GLDM

The GLDM method calculates the Gray level difference method Probability Density functions for the given image. This technique is usually used for extracting statistical texture features of a digital mammogram. From each density functions five texture features are defined: Contrast, Angular Second moment, Entropy, Mean and Inverse Difference Moment.Contrast is defined as the difference in intensity between the highest and lowest intensity levels in an image thus measures the local variations in the grey level. Angular second moment is a measure of homogeneity. If the difference between gray levels over an area is low then those areas are said to be having higher ASM values. Mean it gives the average intensity value. Entropy is the average information per intensity source output. This parameter measures the disorder of an image. When the image is not texturally uniform, entropy is very large. Entropy is strongly, but inversely, correlated to energy. Inverse difference moment IDM measures the closeness of the distribution of elements in the Gray level Co-occurrence Matrix (GLCM) to the GLCM diagonal. To describe the Gray level difference method, let g (n,m) be the digital picture function. For any given displacement δ=(Δn, Δm),where Δn and Δm are integers, let gδ (n,m)=|g(n,m)-g(n+ Δn,m+ Δm)|. Let f(|δ) be the estimated probability density function associated with the possible values of gδ,ie, f(i|δ)=P(gδ(n,m)=i herein our possible forms of vector δ will be considered,(0,d),(-d,d),(d,0),(-d,d),where d is inter sample distance. we refer f(|δ) as gray level difference density function.

Gabor Texture Feature

Gabor texture feature is a linear filter .Basically, Gabor texture feature is a group of wavelets, with each wavelet capturing energy at a capturing energy at a specific frequency and a specific direction. From this group of energy distributions the texture feature representing the image can be extracted. Thus a set of Gabor filters with different frequencies and orientations may be helpful for extracting useful features from an image. Gabor filters have been widely used in pattern analysis applications. Frequency (scale) and orientation representations of Gabor filters are similar to those of the human and mammalian visual system, and they have been found to be particularly appropriate for texture analysis.

CLASSIFICATION METHODS

There are innumerous classification methods for automated classification of samples. In this paper it’s decided to work with most popular classification algorithm: SVM and K-NN

SVM

The Support Vector machines were introduced by Vladimir Vapnik and colleagues. Support Vector machines (SVM’s) are a relatively new learning method used for binary classification. The basic idea is to find a hyper plane which separates the D-Dimensional data perfectly into its two classes. However, since example data is often not linearly separable, SVM’s introduce the notion of a kernel induced feature space which casts the data into a higher dimensional space where the data is separable. Namely, the primary goal of SVM classifiers is classification of examples that belong to one of two possible classes.

However, SVM classifiers could be extended to be able to solve multiclass problems as well. One of the strategies for adapting binary SVM classifiers for solving multiclass problems is one-against-all (OvA) scheme. It includes decomposition of the M-class problem (M>2) into series of two-class problems. The basic concept is to construct M SVMs where the i-th classifier is trained to separate the class i from all other (M-1) classes. This strategy has a few advantages such as its precision, the possibility for easy implementation and the speed in the training phase and the recognition process. That is reason for its wide use.

K-NN

In pattern recognition, the k-nearest neighbour algorithm (k-NN) is a method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until classification. The k-nearest neighbour algorithm is amongst the simplest of all machine learning algorithms: an object is classified by a majority vote of its neighbors,with the object being assigned to the class most common amongst its k nearest neighbours (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of its nearest neighbour. The training examples are vectors in a multidimensional feature space, each with a class label. The training phase of the algorithm consists only of storing the feature vectors and class labels of the training samples. In the classification phase, k is a user-defined constant, and an unlabeled vector (a query or test point) is classified by assigning the label which is most frequent among the k training samples nearest to that query point.

RESULT

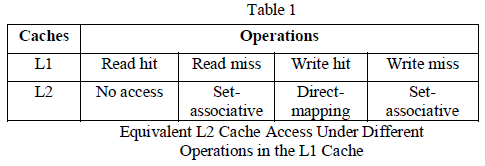Table I. Classification precision for the two-class problem

Table I depicts the classification precision of two classifiers in two class problem with the GLDM descriptor. The results show that GLDM descriptor for various displacements with SVM classifier provides the best classification accuracy of 95.83% .Thus as displacements in GLDM are increased we get the best classification accuracy. In case of GLDM descriptor with the K-NN classifiers results seen are with maximum accuracy of 50% which is not at par with the SVM and GLDM combination of results with 95.83% .Thus we see the GLDM and SVM combination giving better results than GLDM and K-NN combination.

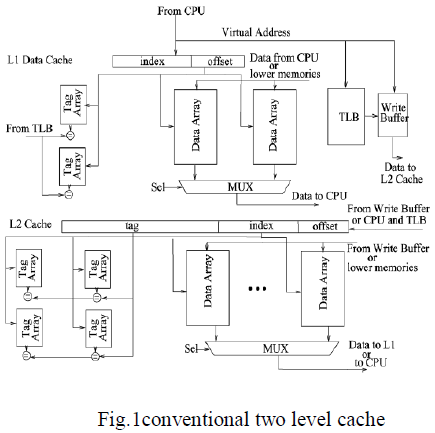Fig 1.GLDM Displacement Verses Percentage Accuracy

The fig 1bar graph above is plotted for table I with x-axis showing Displacements given in GLDM descriptor and yaxis showing percentage accuracy of classifiers such as SVM classifier and K-NN classifier. Here it shows that best classification accuracy is achieved with SVM classifier whose bar graph is shown in blue than bar graph for K-nn classifier shown in red for various displacements in GLDM descriptor.

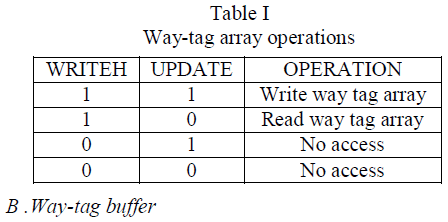Table II.Classification precision for the two-class problem

Table II depicts the classification precision of two classifiers in two class problem with the Gabor texture feature descriptor. The results show that Gabor texture feature descriptor for various orientations with SVM classifier provides the best classification accuracy of 71.83% .Thus as orientations in Gabor are increased we get the best classification accuracy. In case of Gabor texture feature descriptor with the K-NN classifiers results seen are with maximum accuracy of 58.33% which is not at par with the SVM and Gabor texture feature descriptor combination of results with 71.83% .Thus we see the Gabor and SVM combination giving better results than Gabor and K-NN combination.

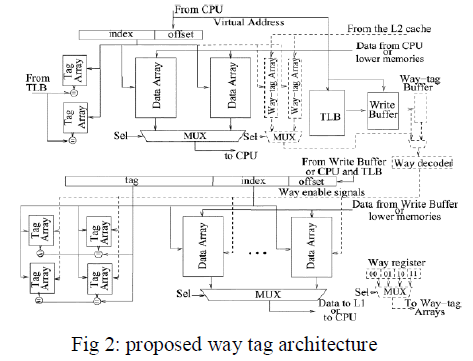The fig 2 bar graph above is plotted for table II with x-axis showing various orientations given in Gabor texture feature descriptor and y-axis showing percentage accuracy of classifiers such as SVM classifier and K-NN classifier. Here it shows that best classification accuracy of 71.83% is achieved with SVM classifier whose bar graph is shown in blue than bar graph for K-nn classifier with percentage accuracy of 58.33% shown in red for various orientations in Gabor texture feature descriptor.

CONCLUSION

Digital mammography is the most common method or early breast cancer detection. Automated analysis of these images is very important, since manual analysis of these images is slow. Today manual analysis of only eight slides of mammography images per day is permitted for the radiologists it being very costly and inconsistent.

In this paper we made analysis on two classifiers, using two different descriptors for feature extraction. According to the examination, we can conclude that the best classification accuracy was achieved, in the case of GLDM descriptor.

References

Majid, E. de Paredes, R. Doherty, N. Sharma, and X. Salvador, “Missed breast carcinoma: Pitfalls and pearls1,” Radiographics, vol. 23,no. 4, p. 881, 2003.
O. Mangasarian, W. Street, and W. Wolberg, “Breast cancer diagnosisand prognosis via linear programming,” Operations Research, vol. 43,no. 4, pp. 570–577, 1995.
M. Sampat, M. Markey, A. Bovik et al., “Computer-aided detection and diagnosis in mammography,” Handbook of image and video processing,vol. 10, no. 4, pp. 1195–1217, 2005.
R. Strickland and H. Hahn, “Wavelet transforms for detecting microcalcifications in mammograms,” Medical Imaging, IEEE Transactions on, vol. 15, no. 2, pp. 218–229, 1996.
M. Giger, F. Yin, K. Doi, C. Metz, R. Schmidt, and C. Vyborny,“Investigation of methods for the computerized detection and analysis of mammographic masses,” in Proceedings of SPIE, vol. 1233, 1990, p.183
S. Liu and E. J. Delp, “Multiresolution detection of stellate lesions in mammograms,” in In Proceedings of the IEEE International Conference on Image Processing, 1997, pp. 109–112.
D. Brzakovic, X. Luo, and P. Brzakovic, “An approach to automated detection of tumors in mammograms,” Medical Imaging, IEEE Transactions on, vol. 9, no. 3, pp. 233–241, 1990.
A. Mohanty and S. Lenka, “Efficient image mining technique for classification of mammograms to detect breast cancer,” Special Issue of IJCCT, vol. 2, no. 2, p. 3.
L. Martins, A. Santos, A. Silva, and A. Paiva, “Classification of normal, benign and malignant tissues using co-occurrence matrix and bayesian neural network in mammographic images,” in Neural Networks, 2006.SBRN’06. Ninth Brazilian Symposium on. IEEE, 2006, pp. 24–29.
E. Cheng, N. Xie, H. Ling, P. Bakic, A. Maidment, and V. Megalooikonomou, “Mammographic image classification using histogram intersection,” in Biomedical Imaging: From Nano to Macro,2010 IEEE International Symposium on. IEEE, 2010, pp. 197–200.