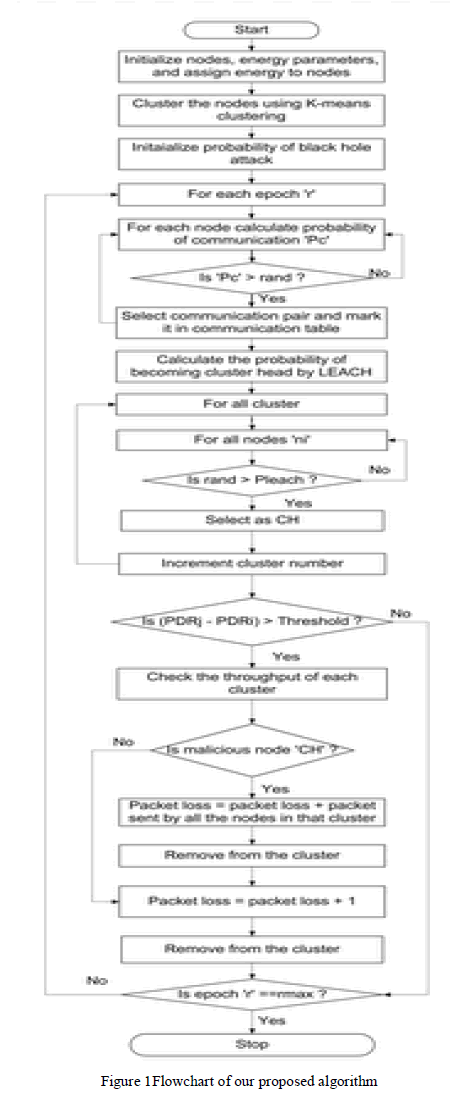
ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
C.Muthamil Selvi1, Dr.K.Gnanambal2 and P.Pon Ragothama Priya*3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The problem of voltage stability is one of the main concern in the operation of power systems. Voltage stability can be determined by determining the maximum loading point of the system. The estimation of voltage stability at various operating condition is essential to operate the system with sufficient safety margin. The objective of this project is to improve the static voltage stability of the power system using SVC emerging CPF algorithm. The voltages at various buses are calculated and the weak buses are identified to place the FACTS devices to improve the voltage stability margin of the system. The voltage stability limits are analyzed before and after the placement of SVC. The IEEE 9 bus system is considered as the test case for this analysis.
Keywords |
| Voltage Stability, Maximum Loadability limit, CPF. |
INTRODUCTION |
| Power system stability is defined as the characteristics of a power system to remain in a state of equilibrium at normal operating condition and restore to an acceptable state of equilibrium after a disturbance [5]. In recent years, power system demand has significantly increased while expanding the power generation and transmission. These increase the transmission line loading. Due to heavy loading of the transmission lines leads to stability problems in the power system. There are various methods available to determine the voltage stability limit. The most familiar method is PV curve. The solutions of load voltages are often presented as a PV curve. |
| The Fig. 1 shows the PV curve, the magnitude of load voltage as a function of real power demand or sum of load demand. |
| The power systems are widely operated in the upper part of the PV curve. The head of the curve is called the maximum loading point. |
 |
| Fig: 1 PV Curve |
| If the system loading increases beyond this point the system will be in unstable position and it is also called as the voltage collapse point. The maximum loadability limit is the margin between the current operating point of the system and the maximum loading point of the system. The load increases beyond the voltage collapse point results in loss of equilibrium and power system can no longer operate. The voltage dependence of loads affects the point of voltage collapse. The power system becomes unstable at the voltage collapse point. The identification of maximum loadability for the power system is described by the various methods [1, 2, 3]. The continuation power flow (CPF) technique has been widely used to determine the maximum loading point of the system. |
| Flexible AC Transmission Systems (FACTS) controllers are mainly used for solving various power system problems [1, 3, 6]. FACTS controllers are widely used to control the voltage, phase angle and impedances of the AC transmission system. SVC is the most promising FACTS controller used to enhance the power system stability. In this paper the maximum loadability limit of the power system has been improved by placing the SVC. |
PROBLEM F ORMULATION |
| The objective of this paper is to determine the maximum loadability limit of a power system without violating the stability limits. The load is increased upto the power flow problem is capable to provide the solution. This can be mathematically formulated as follows, |
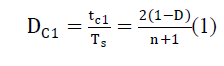 |
CONTINUATION POWER FLOW (CPF) |
| The continuation power flow (CPF) technique has been widely used to determine the maximum loading point of the system. The conventional power flow algorithms are tending to convergence problem at operating points near the stability limit [4, 5]. The CPF analysis overcome this problem and allow user to trace the complete voltage profile by changing the value of loading parameter automatically. The main purpose of using CPF is to find the continuous power flow solutions for a given load change. |
| The CPF principle is simple. It uses the predictorcorrector scheme to find a solution path of a set of power flow equations that have been reformulated to include a load parameter. It starts from a known solution and uses a tangent predictor to estimate a subsequent solution corresponding to a different value of load parameter. This estimation is then corrected using the same Newton- Raphson technique employed by a conventional power flow [4]. |
BASIC PRINCIPLE: |
| The continuation power flow analysis uses an iterative process involving predictor and corrector steps as shown in Fig: 2. It starts from a known initial solution (A), a tangent predictor is used to estimate the solution (B) for a specified pattern of load increase. The corrector step then determines the exact solution (C) using a conventional power flow analysis with system load assumed to be fixed. A new tangent predictor is used to predict the voltage for a further increase in the load. If the new estimate load (D) is now beyond the maximum load on the exact solution, a corrector step with loads fixed would not converge. Therefore a corrector step with a fixed voltage at the monitored bus is applied to find the exact solution (S). As the voltage stability limit is reached, the size of the load increases has to reduce gradually during the successive predictor steps. |
| CPF readings are taken by using the PSAT (Power System Analysis Toolbox) software. It is a Matlab toolbox for analyzing the electric power system analysis [8]. The latest PSAT versions run under Matlab 7.0. |
 |
| Fig.2 Typical sequence of calculations in a CPF analysis |
SVC |
| Static Var Compensator (SVC) is a shunt connected static var generator and/or absorber of reactive power in which the output is varied to maintain the specific parameters of an electrical power system. The SVC has no moving and rotating part like the synchronous compensator. The main purposes of using the SVC in the transmission line are the rapid control of voltage at weak points. The following are the reactive power control elements which character the SVC or part of any SVC. |
| (i) Saturated Reactor (SR) |
| (ii) Thyristor Controlled Reactor (TCR) |
| (iii) Thyristor Switched Reactor (TSR) |
| (iv) Thyristor Switched Capacitor (TSC) |
| (v) Thyristor Controlled Transfer (TCT) |
| (vi) Self /Line commutated converter (SCC or LCC) |
| By using the combinations of these elements, a SVC scheme is provided with any desired control voltage. There are several configurations have been effectively applied to meet the different system requirements. The important considerations in the selection of SVC configuration for any particular application are speed of response, range of size, flexibility, losses and cost. In the simple form, SVC is a combination of fixed capacitor and Thyristor Controlled Reactor configuration as shown in Fig.3. By using shunt capacitors the reactive power generation increases as the square of the bus voltage. |
 |
| SVC controls the network voltages at its coupling point to the system. The SVC provides various control features like Voltage control, Damping of power system oscillations and Reactive power compensation. |
PSAT |
| PSAT is a Matlab toolbox for electrical power system analysis and control [8]. For the analysis purpose the PSAT is user friendly software. In PSAT power flow analysis is performed initially after that the static and dynamic analysis are carried out. These routines are, |
| (i) Continuation power flow |
| (ii) Optimal power flow |
| (iii) Small signal stability analysis |
| (iv) Phasor measurement unit (PMU) placement. |
| When compared to the other Matlab toolboxes PSAT provides various analysis features like PF, CPF, OPF, SSSA and Time domain analysis (TDS) along with the Graphical user interface (GUI). |
CASE STUDY |
| The proposed CPF algorithm is applied to determine the maximum loadability limit of the IEEE 9 bus systems. The studies are performed before and after placement of SVC. The readings are taken from PSAT 1.3.4 in MATLAB 7.0. |
| IEEE 9 bus system |
| The IEEE 9 bus system consists of 3-Generators buses, 6-Load buses and 9-transmission lines [7]. |
| A) Case 1: Before placement of SVC |
| The Conventional CPF algorithm is applied to determine the maximum loadability limit. |
| Table 1 shows the magnitude and phase angle of bus voltages and the maximum loadability limit of the system. The weak bus is identified to place the SVC to improve the maximum loadability limit and voltage profile of the system. Fig.4 shows the PV curve of the system. |
| TABLE 1: RESULTS OF CPF (BEFORE SVC PLACEMENT) |
 |
| From the above obtained results, the 9th bus is identified as weak bus. The SVC placement is carried out in the identified weak bus to improve the maximum loadability limit of the system. |
 |
| Fig.4 PV Curve of the IEEE 9 bus system |
| B) Case 2: After the placement of SVC (with different ratings) |
| For this case the placement of SVC is carried out with the different ratings (20 MVAr, 40MVAr and 50 MVAr). Table 2 shows the magnitude and phase angle of bus voltages and the maximum loadability limit of the system after the placement of SVC with 20MVAr. Fig. 5 shows the PV curve of IEEE 9 bus system with the placement of SVC rating 20MVAr. |
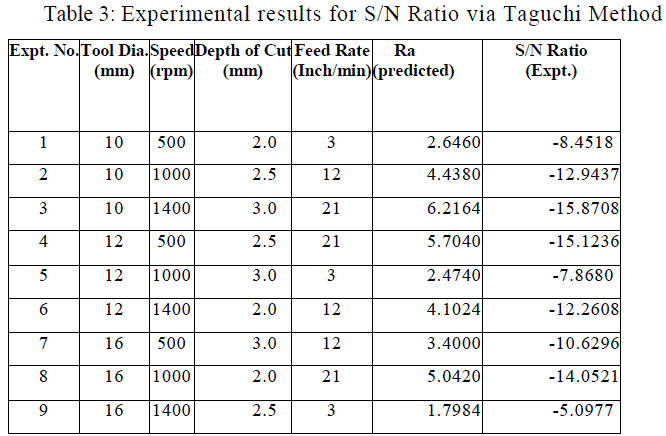
| Table 3 shows the magnitude and phase angle of bus voltages and the maximum loadability limit of the system after the placement of SVC with 40MVAr. Fig. 6 shows the PV curve of IEEE 9 bus system with the placement of SVC rating 40MVAr. |
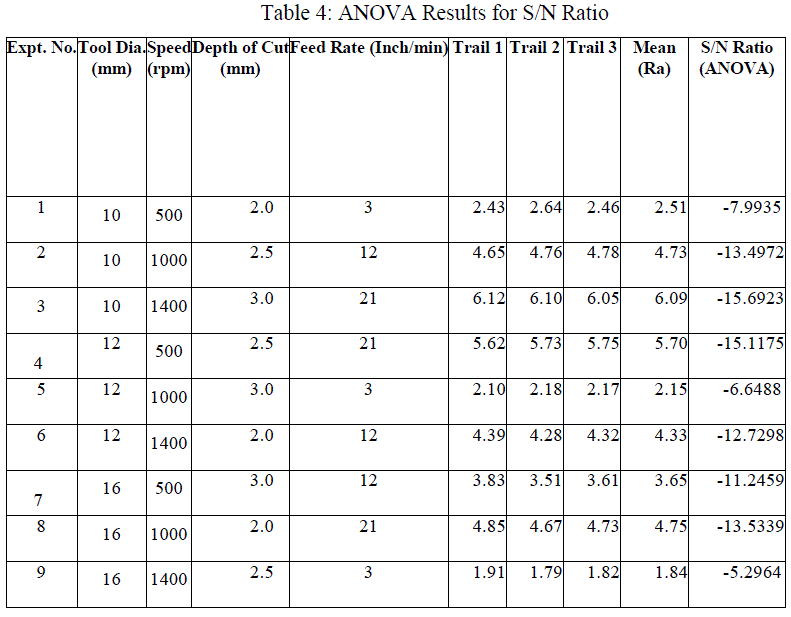
| Table 4 shows the magnitude and phase angle of bus voltages and the maximum loadability limit of the system after the placement of SVC with 50MVAr. Fig. 7 shows the PV curve of IEEE 9 bus system with the placement of SVC rating 50MVAr. |
| TABLE 2: RESULTS OF CPF (AFTER THE PLACEMENT OF SVC WITH 20 MVAr) |
 |
 |
| Fig.5 PV Curve of the IEEE 9 bus system with SVC rating 20MVAr |
| TABLE 3: RESULTS OF CPF (AFTER THE PLACEMENT OF SVC WITH 40 MVAr) |
 |
 |
| Fig.6 PV Curve of the IEEE 9 bus system with SVC rating 40MVAr |
| TABLE 4: RESULTS OF CPF (AFTER THE PLACEMENT OF SVC WITH 50 MVAr) |
 |
 |
| Fig.7 PV Curve of the IEEE 9 bus system with SVC rating 50MVAr |
| TABLE 5: LOADABILITY OF THE SYSTEM WITH DIFFERENT SVC RATING |
 |
| Table 5 shows the loadability limit of the given system before and after placement of SVC. From the above results the maximum loadability limit of the power system is achieved by using SVC. From the results obtained, it is clear that the maximum loadability has been improved while using SVC with 50MVAr. |
CONCLUSIONS |
| In this paper SVC is used to improve the voltage stability margin of system with the help of CPF algorithm. The proposed algorithm has been tested on IEEE 9 bus system. The CPF algorithm results are obtained with before and after the placement of SVC. The improvement of voltage stability margin is achieved with the placement of SVC with 50MVAr. |
References |
|