ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Rajendran. T1 and Gomathi. D2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper introduces a novel approach, i.e. block oriented – restoration, based on a family of Full Range Autoregressive (FRAR) model to restore the information lost, and this adopts the Bayesian approach to estimate the parameters of the model. The Bayesian approach, by combining the prior information and the observed data known as posterior distribution makes inferences. The loss of information caused is due to errors in communication channels, through which the data are transmitted. Even if there is loss of a single bit in a block, it causes loss in the whol block and the impact may reflect on its consecutive blocks. In the proposed technique, such damaged blocks are identified, and to restore it a priori information is searched and extracted from undamaged regions of the image; this information and the pixels in the neighboring region of the damaged block are utilized to estimate the parameters. The estimated parameters are employed to recover the damaged block. The proposed algorithm takes advantage of the linear dependency of the neighboring pixels of the damaged block and takes them as source to predict the pixels of the damaged block. The restoration is performed at two stages: first, the lone blocks are restored; second, the contiguous blocks are restored. It produces very good results and is comparable with other existing schemes.
INTRODUCTION |
| This article addresses the problem of disocclusion or inpainting in color images. The basic idea is to fill in the gap of missing data in a form that it is non-detectable by an ordinary observer; this type of process is called inpainting. In last decade, the Internet and TV usage has rapidly increased and it causes traffic jam in data transmission. To avoid this problem, several imagecoding algorithms have been developed to reduce the bit rate considerably for image and video representation, and transmission. Among them, block-based techniques have proved to be the most appropriate, for instance, Joint Photographic Experts Group (JPEG) [1], Motion Picture Expert Group (MPEG) [2] and H.261 [3]. The data may be corrupted while transmitting them through real-world communication channels, because the channels are not error free. Block-based image coding systems are vulnerable to transmission impairment. The loss of a single bit often results in loss of a whole block and may cause consecutive block losses [4]. This kind of degradation or damage occurs in a variety of domains of applied science and engineering such as visual communications, medical diagnostics, atmospheric remote sensing and astronomy. This motivated as to provide a novel technique which is block oriented. |
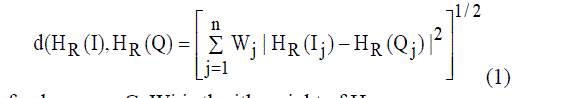 |
| The model based approaches such as Autoregressive (AR) [5, 10], Autoregressive Moving Average (ARMA) [9] and Markov Random Field models [11] have become popular due to their simplicity and appropriateness of image restoration, in-painting and texture synthesis. Error concealment algorithm [4, 12-15] plays a significant role in image restoration problem and is known as low-pass filter, in which the missing information is masked to create subjectively acceptable image. Most techniques use Bayesian approach to estimate the parameters of the model a fore mentioned. The Bayesian analysis is performed in general by combining the prior information and the observed data known as the posterior distribution, from which all the inferences are made [16]. First, Morris [17] proposed the Bayesian approach to resolve this data fusion aspect of combining different sorts of prior information. This approach was subsequently used by many authors [16,18-20] in a unified framework that treats motion, missing data and noise jointly, and they concluded that the Bayesian approach yields better results compared with other techniques Wang et al 4 proposes the best neighborhood algorithm in which the following points are observed; |
| i) This algorithm will work for the periodic pattern textured images only, not for the stochastic pattern and structured images, since there is no guarantee for the same block to be repeated within a particular region. |
| ii) They have not fixed any threshold to decide on the best matching domain block to the range block. Instead they have selected the best one among the blocks belonging to the searching range block. |
| iii) So, the selected domain block may or may not be close to the range block. |
| To overcome these problems, a novel technique based on FRAR model with Bayesian approach, is proposed, which adopts block oriented restoration in color images. In the proposed approach, three different types of blocks, namely damaged block, range block and priorinformation block are used to identify the prior information. The best- matched block of the range block is searched throughout the whole image. The bestmatched block is called prior-information block, and the information available with that block is utilized to estimate the parameters of the FRAR model. Based on the estimated parameters and the pixels in the neighboring region of the damaged block, the pixels in the damaged block are predicted. The obtained results are compared with the existing results of the error concealment algorithms such as without concealment, de-concealment, direct BNM and 1-order BNM algorithms. |
THE PROPOSED MODEL |
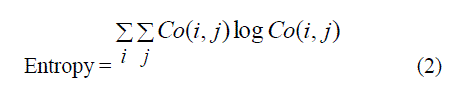 |
| Hence, based on the definitions, the given image is modeled as an Autoregressive (AR) random field. The restoration of the corrupted image region can be performed by utilizing the information available on the uncorrupted regions. Thus, based on the above definitions and the properties of the AR model, it is concluded that an AR model is most appropriate for restoration problem. The main properties of the AR model: (i) future values may depend on the present and the whole past; (ii) future values may not depend on the present and a few past values alone; (iii) facilitates to describe both short-term and long-term correlations. Therefore, this paper utilizes the properties to restore the damaged blocks (assumed to be future values as per properties) from its neighboring region (assumed to be past values as per properties), because the image region is mostly linearly dependent (correlated). |
 |
 |
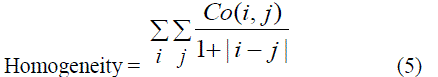 |
PARAMETER ESTIMATION |
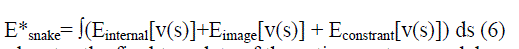 |
| The above joint probability density function can be written as |
 |
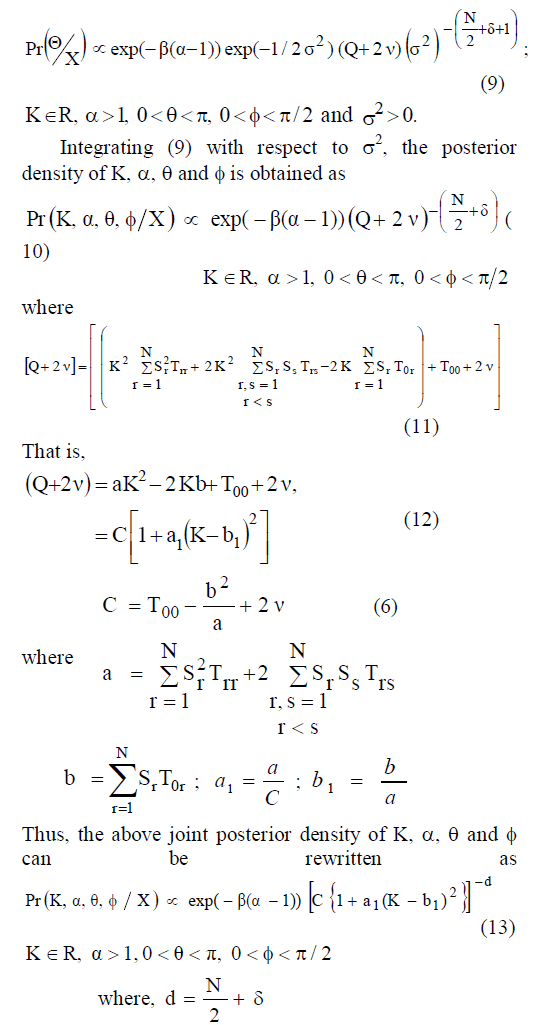 |
| This shows that, given α, θ and φ the conditional distribution of K is ‘t’ distribution located at b1 with (2d– 1) degrees of freedom. |
| The proper Bayesian inference on K, α, θ and φ can be obtained from their respective posterior densities. The joint posterior density of α, θ and φ that is, Pr(α, θ and φ / |
 |
DAMAGED BLOCK AND PRIOR INFORMATION IDENTIFICATION |
| To identify the damaged blocks in the corrupted input image, the image is divided into various blocks of size 8ïÃâô8 and the statistics mean and variance are computed on each block and that are applied in the confidence interval expressed in equation (1). The value of σ2 is compared to that of the lower and upper limits as in equation (1). If the σ2 is less than the lower point then the block is assumed to be damaged because most values in the damaged block are nearer close or same, so there exist less variation among the pixels in the damaged block; if the σ2 is greater than the upper point then the block is assumed to be partially damaged (combination of damaged and undamaged blocks) because the pixel values are in the low and high ranges (i.e. 0 to 255), so there exist high variation; otherwise, the block is treated as undamaged because the pixels belong to the group of moderate intensity values, so there exist moderate variation. In the case of partially damaged block, the region growing technique [28] is adopted to identify the boundary of the damaged block. |
 |
| estimate the hyper-parameters of the prior distributions of the FRAR model parameters. The searching and matching methodology of the prior information is illustrated in Figures 1. A detailed procedure to identify the damaged block and the prior information is presented in an algorithmic form in section 5. |
 |
| Based on the prior-information and the pixels in the neighboring region, the parameters of the FRAR model are estimated. The proposed model is employed to restore the damaged block by using the pixels in the neighboring region as source. The proposed restoration model is discussed in detail in the next section. |
IMAGE RESTORATION |
| The proposed model takes advantage of the linear dependency among the pixels in a particular region. The estimated coefficients and the pixels in the neighboring region are utilized to restore the damaged block, where the layer 1 (outermost layer pixels) of the damaged block is predicted first, and then the layer 2 is predicted. This process is continued for the remaining layers of the damaged block. For instance, to predict a pixel that belongs to the layer 1, a small image region (3 * 3) is considered, which is adjacent to and centered around to the pixel to be predicted (as illustrated in Figure 3). A set of pixels in the immediate neighboring row or column of the damaged block is given maximum weight (order one); the pixels in the adjoining row or column (order two) are given lesser weight than the previous (order one); and the following rows or columns are given lesser weight (order three) than the previous (order two). This paper only considers the first three neighboring rows or columns (up to third order). The methodology adopted to restore the pixels of the damaged block is illustrated in Figure 2. |
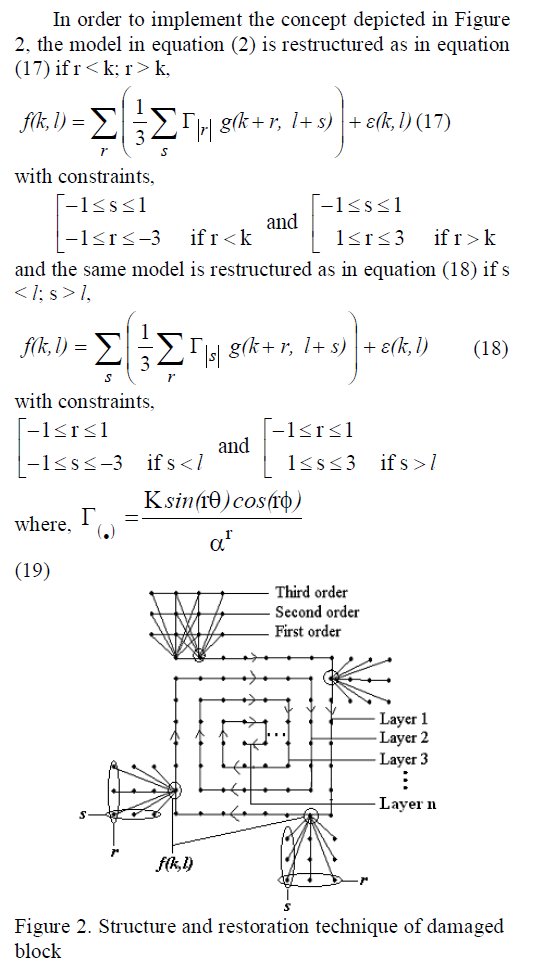 |
EXPERIMENTS AND RESULTS |
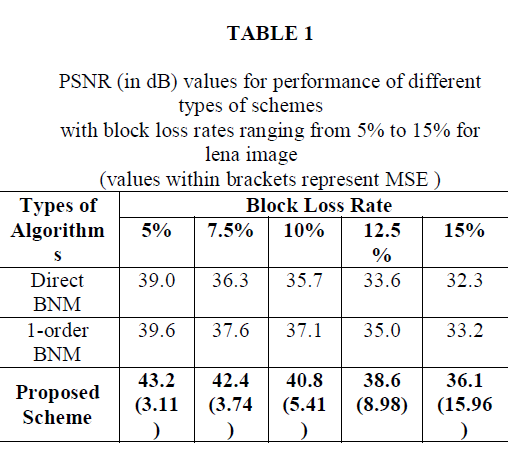
| In order to experiment the proposed FRAR model, different types of color images of size 256 x 256 are considered. Due to the space constraints, for sample, the lena image is presented here. The color image is segregated into RGB colors. On each color image, i.e. RGB color images, the damaged blocks and the prior information are identified as discussed in section 4. Based on the prior information and the pixels in the neighboring region of the damaged block, the parameters K, ïÃÂá, ïÃÂñ and ïÃÂæ are estimated. Applying the parameters in equation (2a), the coefficients ïÃÂÃâ¡rs are computed, and employed to predict the pixels of the damaged block with the use of pixels in the neighboring region as discussed in section 5. The restoration process is performed at two stages: (i) lone blocks are identified and restored; (ii) contiguous blocks are restored. Now, the restored red, green and blue color images are synthesized into RGB color image. The experiment is conducted at various levels of loss of rates ranging from 5% to 15%. The quantitative measures such as PSNR and MSE are computed to the corresponding loss of rates to evaluate the restored image, and they are compared with the existing schemes. The results obtained at various levels of loss of rates are presented in Table 1. The obtained outputs of the experiment conducted on Lena image are shown in below Figure. |
 |
 |
| (a) damaged block of lena image (b) segregated red color of lena image (c) segregated blue color (d) segregated green color (e) restored red color (f) restored blue color (g) restored green color (h) combination of restored red blue and green color gives color image which is similar to original image. |
 |
CONCLUSION |
| This paper adopts an algorithm based on FRAR model and the Bayesian approach to estimate the parameters of the model, which is employed to restore the damaged blocks. The best matching block of the damaged block is searched throughout the whole image. The information available in the best matching block is extracted and used as prior information for actual parameters of the model. The parameters are estimated based on the prior information and the pixels in the neighboring region of the damaged block. The parameters are utilized to restore the damaged block. The proposed algorithm takes advantage of linear dependency of the neighboring pixels of the damaged block and takes them as source to predict the pixels in the damaged block. A structured lena image is considered during the experiment. The performance of the proposed technique is evaluated in terms of quantitative and qualitative measures. The experimental results clearly show that the proposed restoration scheme yields good results. The obtained results are comparable with the existing methods. |
References |
|