Integrating Run Length Encoding and Column oriented database execution using Binary Search Tree

Abstract

Column oriented databases have attracted significant amount of attention recently and database systems based on Column oriented technology are used extensively for analytical processing such as those found in data warehouses, decision support, and business intelligence and forecasting applications. Column oriented databases have enormous potential for data compression because of the similarity of adjacent records. This paper will discuss an algorithm that makes use of this similarity in a column oriented databases to integrate the compression and execution processes. It proposes a new indexing method called Binary Search Tree (BST) indexing that supports O (log n) insertion, deletion and look-up operations. Additionally, the paper also describes the implementation of these basic operations.

Keywords

Column-oriented database, Run-length encoding, Compression, Binary Search Tree, Performance

INTRODUCTION

Column oriented databases are receiving increased attention these days and are used increasingly in analytical and data warehousing applications. This is due to the fact that vertical partitioning of the relation makes faster reads and aggregation possible. In addition, various compression methods like run length encoding and bitmap encoding help to achieve a higher compression ratio in column oriented databases. The performance depends on the level of compression achieved. [1] shows that run length encoding and bitmap encoding schemes are dependent on the ordering of the tuples. Hence out of order insertions typically degrade the compression achieved and consequently the performance of the look-ups.

On average, the time taken to insert or delete a tuple from a relation varies linearly with the number of tuples in a relation. This is because, in addition to the updated tuple, the storage keys or identifiers of the successive tuples have to be updated as well. In addition, the tuples in a read optimized relation need to be decompressed and recompressed after an update operation. This requires additional time. This paper shows that it is possible to perform in-place inserts, deletes and updates in sub-linear time in the number of tuples in the relation by making use of Binary Search Trees. Each node in the Binary Search Tree (BST) contains the value of the attribute and each of these points to a linked list which holds the databases indices, where the attribute is stored. The compression ratio is further improved because the database indices of the tuples are stored along with the tuple attributes.

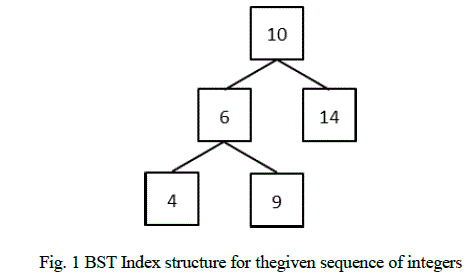
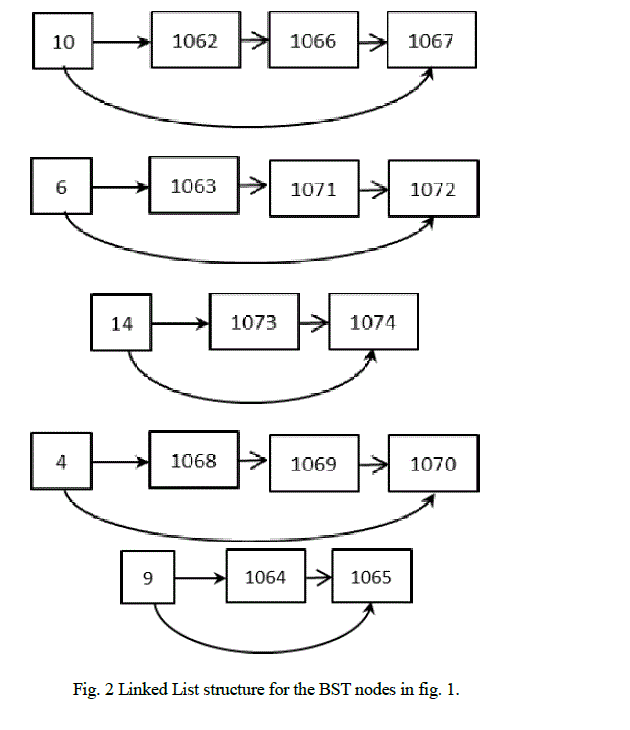
Run-length Encoding Scheme- In column-oriented databases, every attribute in a tuple is stored separately as a sequence of values. These sequences could be run-length encoded or bitmap encoded. The run-length encoding scheme compresses successive repetitions of values or runs in a sequence. There are two ways of representing a successive repetition of values or runs in sequence [2] – count based and offset based representation. Consider the sequence of values 10(1062), 6(1063), 9(1064), 9(1065), 10(1066), 10(1067), 4(1068), 4(1069), 4(1070), 6(1071), 6(1072), 14(1073), 14(1074). The integers in the brackets (starting from 1062) represent the database indices associated with the tuples of which, the attributes are a part. If we use the count based representation of runs to encode this sequence, we would get (10,1), (6,1), (9,2), (10,2), (4,3), (6,2), (14,2) as the result. Instead if we use offset based representation, we would get (10,1), (6,2), (9,4), (10,6), (4,9), (6,11), (14,13).

The organization of this paper is described as below.

1. Section II lists down the related works that were referred in this journal.

2. Section III.A defines BST indices and explains how a BST index is created for the example sequence shown above.

3. Section III.B explains how the basic operation like look-up, insertion, deletion, and updating is carried out on a BST index.

BACKGROUND AND RELATED WORKS

A. Database Compression

Database compression is an effective way of saving space and reducing disk I/O. Many compression schemes have been devised based on character encoding or detection of repetitive strings.

Dictionary coding [2] is a compression technique that uses character encoding to compress the data. All the distinct values are written into the dictionary, and they are encoded as tokens that act as their indexes in the data dictionary. These tokens occupy less space than the data, and replace all their occurrences, which results in compression. For example, if an attribute that consumes 5 bytes of space has only 8 distinct values, they can be replaced by tokens, each of 3 bits in length. Decompression involves only searching the dictionary for the data using its token as an index, so it has a very high decompressing performance.

Run-length encoding (RLE) [3] is a simple form of data compression that converts the runs of data (the sequences in which same value occurs consecutively) into a (value, length) pair. The pair (v, n) denotes that the value „v‟ has repeated consecutively for „n‟ number of times. For example, consider the sequence: a,a,a,a,b,b,b,a,a,b,b,b,b. This sequence can be compressed as: (a,4),(b,3),(a,2),(b,4) using RLE technique. The performance of this compression method depends on the length of the run. Longer the run, higher will be the compression ratio.

Besides the ones mentioned above, there are other compression approaches used in real systems such as null suppression, delta coding, bit packing [2][4], et al.

B. Row-oriented storage, Column-oriented storage, Compression

Traditional databases use row-oriented storage, in which an entire record is stored as a single entity. A relatively new approach is the column-oriented storage [5], where all the values of a column are stored together, instead of records. Both the approaches have their own benefits and limitations. For example, if a record has to be inserted or deleted from the table, the row-oriented database can achieve it within a single disk seek, while column-oriented database requires multiple disk seeks, as the columns of a record are stored separately. On the other hand, if an aggregate has to be computed, only the required column needs to be accessed, instead of the entire record. So, row-oriented database is suitable for transaction processing, whereas column-oriented database performs better in analytics.

Data compression plays a cardinal role in query processing, as it reduces disk I/O. The adjacent columns of a record may have different value domains. When these values are stored together as in row-oriented storage, value locality on the page becomes very poor. So, row-oriented storage has only a little potential for compression. On the contrary, as the column data is of uniform type, and same values can occur repeatedly, column-oriented data is more compressible than its counterpart. As a result, performance optimization of the column-store in transactional operations, and new encoding schemes for compression has become areas of active research.

A notable contribution in columnar compression and execution is given by [3]. It proposes an indexing scheme called count indexes that supports in-place insertions, deletions, updates and look ups on a run-length encoded sequence with n runs in time that is sub-linear in the number of tuples. This is achieved by maintaining the count index as a binary tree, where (value, length) pairs of the sequence form the leaf nodes, and the interior nodes store the sum of the „length‟ of their children. Thus, the root node stores the total number of elements in the sequence. In this paper, we present a new indexing scheme called Binary Search Tree (BST) indexing, which also makes use of run-length encoding (RLE) technique. Representing the sequence as a binary search tree makes it possible to carry out all the operations – insert, update and delete, in O(log n) time for n runs.

BINARY SEARCH TREE INDEX

A. Definition

A BST index on a sequence of integers along with their database indices is defined as a binary search tree structure which contains the integers in its nodes. The database indices are maintained as linked lists for each node of the main tree. The sample BST index structure for the sequence of integers mentioned in the introductory section is shown below.

The pseudo code for insertion operation is as follows:

Insert (root, value, db_index)

2) Deletion

The deletion of an entry from the database is achieved by removing the corresponding database index from the BST node of the entry. Deletion can take place under the following scenarios:

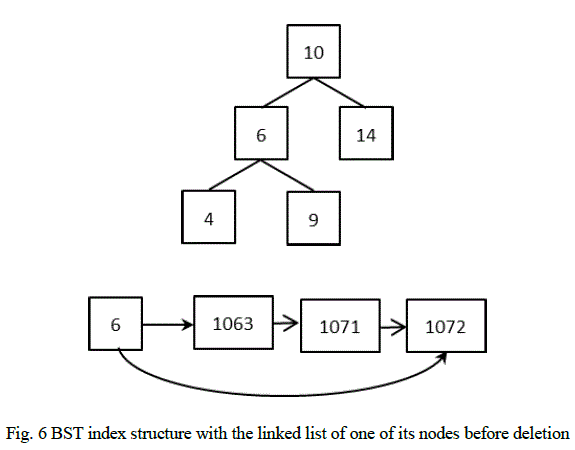
2.1) When the index from which the value has to be deleted is not the only index, to which the node points: Currently the BST index would look like the following.

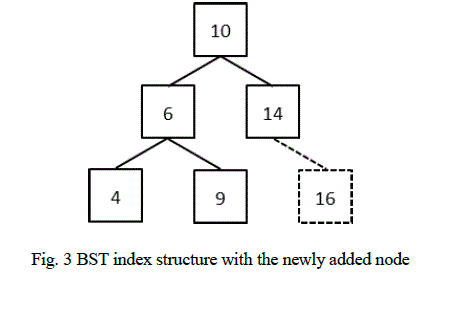For e.g., if the index: 1071 of node „6‟ has to be deleted, the node „6‟ is first located in BST using BST look up algorithm. Once it is found, its linked list of indices is searched for the index: 1071. Deleting this index from the linked list implies that the value „6‟ no more exists in the location given by the index. After deletion, the BST will remain unchanged. The linked list of node „6‟ would be as follows:

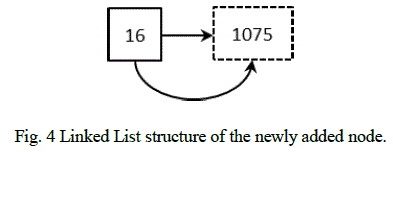3) Updating

When a database entry is updated to a new value, corresponding changes have to be made in the BST index. There are two types of changes that could result due to a database update.

3.1) When the new value of the field already exists in the BST index as part of another node.

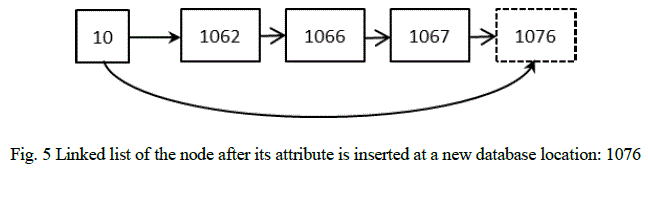
In this case, a node is deleted from the linked list associated with the old value and a node is inserted to the linked list associated with the new value. For e.g., if the attribute value 10 at database index 1066 is updated to 6, the resultant linked list structures are as follows.

CONCLUSION

Column-store has an immense potential for compression due to the similarity of adjacent records. In this paper, we have proposed that a significant level of compression can be achieved without losing out on the performance of the basic operations - insertion, updation and deletion, using a combination of run-length encoding technique and BST indexing representation. Run-length encoding gives a good level of compression, whereas BST indexing performs O (log n) insertion, deletion and look-up operations, for a sequence of n runs. Hence we see this as an important work towards understanding the real potential of column-oriented database.

References

D. J. Abadi, P. A. Boncz, and S. Harizopoulos. “Column-oriented database systems”. Proc. VLDB, 2009. Daniel J. Abadi, Samuel R. Madden, and Miguel C.Ferreira., “Integrating compression and execution in column-oriented database systems,” Proc. SIGMOD 2006, ACM, pp. 671-682, 2006. AbhijeetMohapatra and Michael Genesereth, “Incrementally Maintaining Run-length Encoded Attributes in Column Stores”, IDEAS12, 2012. Allison L. Holloway, and David J. DeWitt, “Read- optimized databases, in depth,” Proc. VLDB 2008, Morgan Kaufmann, 2008, pp. 502-513. M. Stonebraker, et al, “C-Store: a column-oriented DBMS,” Proc. VLDB 2005, Morgan Kaufmann, 2005, pp. 553-564.