ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
K. Ramesh 1, M. Thirumalaiswamy 2 and S.Kavunthi 3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, a new class of sets called intuitionistic fuzzy wgrα-closed sets is introduced and their properties are studied. Moreover the notions of applications of an intuitionistic fuzzy wgrα-closed sets, intuitionistic fuzzy wgrα-continuity and intuitionistic fuzzy wgrα-irresoluteness are introduced
Keywords |
| Intuitionistic fuzzy topology, intuitionistic fuzzy wgrα-closed sets, IFwgr-T1\2 space, IFwgrα-T1\2 space and intuitionistic fuzzy wgrα-continuity. |
| 2010 Mathematics Subject Classification: 54A40, 03F55. |
INTRODUCTION |
| In 1965, Zadeh[12] introduced fuzzy sets and in 1968, Chang[2] introduced fuzzy topology. After the introduction of fuzzy sets and fuzzy topology, several researches were conducted on the generalizations of the notions of fuzzy sets and fuzzy topology. The concept of intuitionistic fuzzy sets was introduced by Atanassov[1] as a generalization of fuzzy sets. In 1997, Coker [3] introduced the concept of intuitionistic fuzzy topological spaces. In this paper, we introduce the concepts of intuitionistic fuzzy wgrα-closed sets, intuitionistic fuzzy wgrα-open sets and intuitionistic fuzzy wgrα-continuity and study some of their properties in intuitionistic fuzzy topological spaces. |
PRELIMINARIES |
| Throughout this paper, (X, τ) or X denotes the intuitionistic fuzzy topological spaces (briefly IFTS). For a subset A of X, the closure, the interior and the complement of A are denoted by cl(A), int(A) and Ac respectively. We recall some basic definitions that are used in the sequel. Definition 2.1: [1] Let X be a non-empty fixed set. An intuitionistic fuzzy set (IFS for short) A in X is an object having the form A = {âßèx, μA(x), νA(x)âßé/ x ∈ X} where the functions μA : X → [0,1] and νA : X → [0,1] denote the degree of membership (namely μA(x)) and the degree of non-membership (namely νA(x)) of each element x∈ X to the set A, respectively, and 0 ≤ μA(x) + νA(x) ≤ 1 for each x ∈ X. Denote by IFS(X), the set of all intuitionistic fuzzy sets in X. |
| Definition 2.2: [1] Let A and B be IFSs of the form A = {âßèx, μA(x), νA(x)âßé/ x ∈ X} and B = {âßèx, μB(x), νB(x)âßé/ x∈ X}. Then |
| (i) A ⊆ B if and only if μA(x) ≤ μB(x) and νA(x) ≥ νB(x) for all x ∈ X, |
| (ii) A = B if and only if A ⊆ B and B ⊆ A, |
 |
| Definition 2.9: An IFS A = {âßè x, μA(x), νA(x) âßé / x ε X} in an IFTS (X, τ) is called an |
| (i) intuitionistic fuzzy generalized closed set (IFGCS for short) if cl(A) ⊆ U whenever A ⊆ U and U is an IFOS[11] |
| (ii) intuitionistic fuzzy α- generalized closed set (IFαGCS for short) if αcl(A) ⊆ U whenever A⊆ U and U is an IFOS in X.[9] |
| (iii) intuitionistic fuzzy generalized semi closed set (IFGSCS for short) if scl(A) ⊆ U whenever A ⊆ U and U is an IFOS [10] |
| (iv) intuitionistic fuzzy regular generalized α-closed set (IFRGαCS for short) if αcl(A) ⊆ U whenever A ⊆ U and U is an IFRαOS in X.[6] |
| An IFS A is said to be an intuitionistic fuzzy generalized open set (IFGOS for short), intuitionistic fuzzy α-generalized open set (IFαGOS for short), intuitionistic fuzzy generalized semi open set (IFGSOS for short) and intuitionistic fuzzy regular generalized α-open set (IFRGαOS for short) if the complement of A is an IFGCS, IFαGCS, IFGSCS and IFRGαCS respectively. |
| Definition 2.10: [7] An IFS A in an IFTS (X, τ) is said to be an intuitionistic fuzzy regular weakly generalized closed set (IFRWGCS for short) if cl(int(A)) ⊆ U whenever A ⊆ U, U is IFROS in X. An IFS A is said to be an intuitionistic fuzzy regular weakly generalized open set (IFRWGOS for short) in (X, τ) if the complement of A is an IFRWGCS in X. |
| Definition 2.11: [4] Let (X, τ) and (Y, σ) be two intuitionistic fuzzy topological spaces and let f âÃËö X→ Y be a function. Then f is said to be an intuitionistic fuzzy continuous if the pre image of each intuitionistic fuzzy open set of Y is an intuitionistic fuzzy open set in X. |
| Definition 2.12: [5] Let f be a mapping from an IFTS (X,τ) into an IFTS (Y,σ). Then f is said to be an (i) intuitionistic fuzzy α-continuous (IFα continuous for short)if f-1 (B) ∈ IFαO(X) for every B ∈ σ, (ii) intuitionistic fuzzy pre continuous (IFP continuous for short) if f -1(B) ∈ IFPO(X) for every B ∈ σ. |
| Definition 2.13: [6] Let (X, τ) and (Y, σ) be two intuitionistic fuzzy topological spaces and let f âÃËö X → Y be a function. Then f is called an intuitionistic fuzzy regular generalized α-continuous (IFRGα continuous for short) if f -1(A) is an IFRGαCS in (X, τ) for every IFCS A of (Y, σ). Definition 2.14: [8] Let f be a mapping from an IFTS (X,τ) into an IFTS (Y,σ). Then f is called an intuitionistic fuzzy regular weakly generalized continuous (IFRWG continuous for short) if f -1(A) is an IFRWGCS in (X, τ) for every IFCS A of (Y, σ). |
INTUITIONISTIC FUZZY wgrα-CLOSED SETS and INTUITIONISTIC FUZZY wgrα-OPEN SETS |
| In this section we introduced intuitionistic fuzzy wgrα-closed set, intuitionistic fuzzy wgrα-open set and have studied some of its properties. |
| Definition 3.1: An IFS A in an IFTS (X,τ) is said to be an intuitionistic fuzzy wgrα-closed set (IFWGRαCS for short) if cl(int(A)) ⊆ U whenever A ⊆ U and U is IFRαOS in X. The complement of the IFWGRαCS is an IFWGRαOS in (X,τ). The family of all IFWGRαCSs of an IFTS (X, τ) is denoted by IFWGRαCS(X). For the sake of simplicity, we shall use the notation A= âßèx, (μ, μ), (ν, ν)âßé instead of A= âßèx,(a/μa, b/μb), (a/νa, b/νb)âßé in all the examples used in this paper. Similarly we shall use the notation B= âßèx, (μ, μ), (ν, ν)âßé instead of B= âßèx,(u/μu, v/μv), (u/νu, v/νv)âßé in the following examples. |
| Example 3.2: Let X = {a, b} and G = âßèx, (0.3, 0.3), (0.7, 0.7)âßé. Then τ = {0~, G, 1~} is an IFT on X and the IFS A = âßèx, (0.2, 0.2), (0.8, 0.7)âßé is an IFWGRαCS in (X, τ). |
| Result 3.3: Every IFROS is an IFRαOS. Proof: Let A be an IFROS in X. Therefore int(cl(A)) = A. Since A ⊆ cl(A) = cl(int(cl(A))) implies A ⊆ A ∪ cl(int(cl(A))) = αcl(A). Therefore A ⊆ A ⊆ αcl(A). Hence A is an IFRαOS. Theorem 3.4: Every IFCS in (X, τ) is an IFWGRαCS in (X, τ) but not conversely. Proof: Let A be an IFCS in (X, τ). Let A ⊆ U and U be an IFRαOS in (X, τ). Since A is an intuitionistic fuzzy closed, cl(A) = A and hence cl(A) ⊆ U. But cl(int(A)) ⊆ cl(A) ⊆ U. Therefore cl(int(A)) ⊆ U. Hence A is an IFWGRαCS in (X, τ). Example 3.5: Let X = {a, b} and G = âßèx, (0.3, 0.3), (0.7, 0.7)âßé. Then τ = {0~, G, 1~} is an IFT on X and the IFS A = âßèx, (0.2, 0.2), (0.8, 0.7)âßé is an IFWGRαCS but not an IFCS in X. Theorem 3.6: Every IFRCS in (X, τ) is an IFWGRαCS in (X, τ) but not conversely. Proof: Let A be an IFRCS in (X, τ). Let A ⊆ U and U be an IFRαOS in (X, τ). Since A is IFRCS, cl(int(A)) = A ⊆ U. This implies cl(int(A)) ⊆ U. Hence A is an IFWGRαCS in (X,τ). Example 3.7: In Example 3.2., the IFS A = âßèx, (0.2, 0.2), (0.8, 0.7)âßé is an IFWGRαCS but not an IFRCS in (X, τ). Theorem 3.8: Every IFαCS in (X, τ) is an IFWGRαCS in (X, τ) but not conversely. Proof: Let A be an IFαCS in (X, τ). Let A ⊆ U and U be an IFRαOS in (X, τ). By hypothesis, cl(int(cl(A))) ⊆ A. Therefore cl(int((A)) ⊆ cl(int(cl(A))) ⊆ A ⊆ U. Therefore cl(int((A)) ⊆ U. Hence A is an IFWGRαCS in (X, τ). Example 3.9: In Example 3.2., the IFS A = âßèx, (0.2, 0.2), (0.8, 0.7)âßé is an IFWGRαCS but not an IFαCS in (X, τ). Theorem 3.10: Every IFPCS in (X, τ) is an IFWGRαCS in (X, τ) but not conversely. Proof: Let A be an IFPCS in (X, τ). Let A ⊆ U and U be an IFRαOS in (X, τ). By definition, cl(int(A)) ⊆ A and A ⊆ U. Therefore cl(int(A) ⊆ U. Hence A is an IFWGRαCS in X. Example 3.11: Let X = {a, b} and G = âßèx, (0.7, 0.9), (0.3, 0.1)âßé. Then τ = {0~, G, 1~} is an IFT on X and the IFS A = G is an IFWGRαCS but not an IFPCS in (X, τ). Theorem 3.12: Every IFRGαCS in (X, τ) is an IFWGRαCS in (X, τ) but not conversely. Proof: Let A be an IFRGαCS in (X, τ). Let A ⊆ U and U be an IFRαOS in (X, τ). By definition, αcl(A) = A ∪ cl(int(cl(A))) ⊆ U. This implies cl(int(cl(A))) ⊆ U and cl(int(A)) ⊆ cl(int(cl(A))) ⊆ U. Therefore cl(int(A)) ⊆U. Henece A is an IFWGRαCS in (X, τ). Example 3.13: In Example 3.2., the IFS A = âßèx, (0.2, 0.2), (0.8, 0.7) âßé is an IFWGRαCS but not an IFRGαCS in (X, τ). |
| Theorem 3.14: Every IFWGRαCS in (X, τ) is an IFRWGCS in (X, τ) but not conversely. |
| Proof: Let A be an IFWGRαCS in (X, τ). Let A ⊆ U and U be an IFROS in (X, τ). Since every IFROS is an IFRαOS and by hypothesis cl(int(A)) ⊆U. Hence A is an IFRWGCS in (X, τ). |
| Example 3.15: Let X = {a, b} and G = âßèx, (0.2, 0.3), (0.5, 0.6)âßé. Then τ = {0~, G, 1~} is an IFT on X and the IFS A = âßèx, (0.4, 0.4), (0.5, 0.4)âßé is an IFRWGCS but not an IFWGRαCS in (X, τ). Proposition 3.16: IFSCS and IFWGRαCS are independent to each other which can be seen from the following example. Example 3.17: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.5, 0.2), (0.5, 0.6)âßé. Then the IFS A = G is an IFSCS but not an IFWGRαCS in X. Example 3.18: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.3, 0.3), (0.7, 0.7)âßé. Then the IFS A = âßèx, (0.2, 0.2), (0.8, 0.7)âßé is an IFWGRαCS but not an IFSCS in X. Proposition 3.19: IFGSCS and IFWGRαCS are independent to each other which can be seen from the following example. Example 3.20: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.5, 0.2), (0.5, 0.6)âßé. Then the IFS A = G is an IFGSCS but not an IFWGRαCS in X. Example 3.21: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.7, 0.9), (0.3, 0.1)âßé. Then the IFS A = âßèx, (0.6, 0.7), (0.4, 0.3)âßé is an IFWGRαCS but not an IFGSCS in X. Proposition 3.22: IFGCS and IFWGRαCS are independent to each other which can be seen from the following example. Example 3.23: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.5, 0.2), (0.5, 0.6)âßé. Then the IFS A = âßèx, (0.5, 0.3), (0.5, 0.6)âßé is an IFGCS but not an IFWGRαCS in X. Example 3.24: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.3, 0.3), (0.7, 0.7)âßé. Then the IFS A = âßèx, (0.2, 0.2), (0.8, 0.7)âßé is an IFWGRαCS but not an IFGCS in X. Proposition 3.25: IFWGCS and IFWGRαCS are independent to each other which can be seen from the following example. Example 3.26: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.5, 0.2), (0.5, 0.6)âßé. Then the IFS A = âßèx, (0.5, 0.3), (0.5, 0.6)âßé is an IFWGCS but not an IFWGRαCS in X. Example 3.27: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.8, 0.9), (0.2, 0.1)âßé. Then the IFS A = âßèx, (0.7, 0.8), (0.3, 0.2)âßé is an IFWGRαCS but not an IFWGCS in X. Proposition 3.28: IFαGCS and IFWGRαCS are independent to each other which can be seen from the following example. Example 3.29: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.5, 0.2), (0.5, 0.6)âßé. Then the IFS A = âßèx, (0.5, 0.3), (0.5, 0.6)âßé is an IFαGCS but not an IFWGRαCS in X. |
| Example 3.30: Let X = {a, b} and let τ = {0~, G, 1~} be an IFT on X, where G = âßèx, (0.8, 0.9), (0.2, 0.1)âßé. Then the IFS A = âßèx, (0.7, 0.8), (0.3, 0.2)âßé is an IFWGRαCS but not an IFαGCS in X. The following implications are the relations between intuitionistic fuzzy weakly generalized regular α-closed set and other existing intuitionistic fuzzy closed sets: |
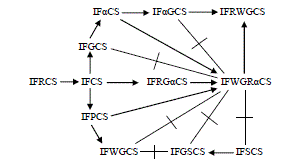 |
| In this diagram by “A B” we mean A implies B but not conversely and “A B” means A and B are independent of each other. |
| Remark 3.31: The union of any two IFWGRαCSs in (X, τ) is not an IFWGRαCS in (X, τ) in general as seen from the following example. |
| Example 3.32: Let X= {a, b} and let τ= {0~, G, 1~} where G = âßèx, (0.3, 0.3), (0.7, 0.7)âßé. Then the IFSs A = âßèx, (0.2, 0.4), (0.8, 0.6)âßé and B = âßèx, (0.3, 0.2), (0.7, 0.8)âßé are IFWGRαCSs in (X, τ) but A ∪ B = âßèx, (0.3, 0.4), (0.7, 0.6)âßé is not an IFWGRαCS in (X, τ). Let U = âßèx, (0.3, 0.4), (0.7, 0.6)âßé be an IFRαOS in (X, τ). Since A∪B ⊆ U but cl(int(A∪B)) âÃÅ ÃËU. |
| Remark 3.33: The intersection of any two IFWGRαCSs in (X, τ) is not an IFWGRαCS in (X, τ) in general as seen from the following example. |
| Example 3.34: Let X= {a, b} and let τ = {0~, G, 1~} where G = âßèx, (0.3, 0.3), (0.7, 0.7)âßé. Then the IFSs A = âßèx, (0.6, 0.8), (0.4, 0.2)âßé and B = âßèx, (0.9, 0.4), (0.1, 0.6)âßé are IFWGRαCSs in (X, τ) but A∩B =âßèx, (0.6, 0.4), (0.4, 0.6)âßé is not an IFWGRαCS in (X, τ). Let U = âßèx, (0.6, 0.4), (0.4, 0.6)âßé be an IFRαOS in X. Since A∩B ⊆ U but cl(int(A∩B)) âÃÅ ÃË U. Theorem 3.35: Let A be an IFWGRαCS in (X, τ), then cl(int(A))−A does not contain any non-empty IFRαOS. Proof: Let F be a non-empty IFRαOS such that F ⊆ cl(int(A))−A. Then F ⊆ X−A⇒ A⊆ X−F, X−F is an IFRαOS. Since A is an IFWGRαCS, cl(int(A)) ⊆X−F. Therefore F ⊆ cl(int(A)) ∩ X−cl(int(A)), which implies F = υ, which is a contradiction. Hence cl(int(A)) −A does not contain any non-empty IFRαOS. Theorem 3.36: For an element x ∈ X, then the set X−{x} is an IFWGRαCS or IFRαOS. |
| Proof: Suppose X−{x} is not IFRαOS. Then X is the only IFRαOS containing X−{x}⇒ cl(int({X−{x}})) ⊆ X. Therefore X−{x} is an IFWGRαCS. Theorem 3.37: A is an IFWGRαCS of X such that A ⊆ B⊆cl(int(A)), then B is an IFWGRαCS in X. Proof: If A is an IFWGRαCS of X such that A ⊆ B⊆cl(int(A)). Let U be IFRαOS of X such that B ⊆ U, then A ⊆ U. Since A is an IFWGRαCS, cl(int(A)) ⊆U. Now cl(int(B)) ⊆cl(int(cl(int(A)))) = cl(int(A)) ⊆ U. Thus B is an IFWGRαCS in X. Theorem 3.38: If A is an IFWGRαCS and an IFROS, then A is an IFRGCS. Proof: Let A ⊆ U and U be an IFROS. By hypothesis, cl(A) ⊆ U. Therefore A is an IFRGCS. Theorem 3.39: Let A be an IFWGRαCS in (X, τ), then A is an IFRCS iff cl(int(A)) −A is an IFRαOS. Proof: Suppose A is an IFRCS in X. Then cl(int(A)) = A and so cl(int(A))−A = υ, which is an IFRαOS in X. Conversely, Suppose cl(int(A))−A is an IFRαOS in X. Then cl(int(A)) −A = υ. Hence A is an IFRCS in X. |
| Theorem 3.40: A subset A of a topological space X is an IFWGRαOS iff F⊆int(cl(A)), whenever F is an IFRαOS and F ⊆ A. |
| Proof: Assume A is an IFWGRαOS, Ac is an IFWGRαCS. Let F be an IFRαOS in X contained in A. Fc is an IFRαOS in X containing Ac. Since Ac is an IFWGRαCS, cl(int(Ac) ⊆ Fc . Therefore F ⊆ int(cl(A)). Conversely, let F ⊆int(cl(A)) whenever F ⊆ A and F is an IFRαOS in X. Let G be an IFRαOS containing Ac then Gc ⊆ int(cl(A)). Thus cl(int(Ac)) ⊆G ⊆Ac is an IFWGRαCS ⊆ A is an IFWGRαOS. |
| Theorem 3.41: If A ⊆ X is an IFWGRαCS, then cl(int(A)) −A is an IFWGRαOS. |
| Proof: Let A be an IFWGRαCS and F be an IFRαOS. F ⊆ cl(int(A)) −A, then int(cl((cl(int(A)) − A))) = υ. Thus F ⊆ int(cl((cl(int(A)) − A))). Therefore cl(int(A)) − A is an IFWGRαOS. |
| Theorem 3.42: If int(cl(A)) ⊆B⊆A and A is an IFWGRαOS, then B is an IFWGRαOS. |
| Proof: Let int(cl(A)) ⊆B ⊆ A. Thus X−A ⊆ X−B ⊆ cl(int(X−A)). Since X−A is an IFWGRαCS, by theorem 3.37, X−B is an IFWGRαCS. |
INTUITIONISTIC FUZZY wgrα-CONTINUOUS MAPPINGS and INTUITIONISTIC FUZZY wgrα-IRRESOLUTE MAPPINGS |
| Definition 4.1: A mapping f: (X, τ) → (Y, σ) is called an intuitionistic fuzzy wgrα-continuous (IFWGRα continuous for short) mappings if f -1(V) is an IFWGRαCS in (X, τ) for every IFCS V of (Y, σ). Example 4.2: Let X= {a, b}, Y= {u, v} and G1 = âßèx, (0.3, 0.3), (0.7, 0.7)âßé, G2 = âßèy, (0.8, 0.7), (0.2, 0.2)âßé. Then τ = {0~, G1, 1~} and σ = {0~, G2, 1~} are IFTs on X and Y respectively. Define a mapping f: (X, τ) → (Y, σ) by f(a) = u and f(b) = v. Then f is an IFWGRα-continuous mapping. Definition 4.3: A mapping f: (X, τ) → (Y, σ) is called an intuitionistic fuzzy wgrα-irresolute (IFWGRα irresolute for short) mappings if f -1(V) is an IFWGRαCS in (X, τ) for every IFWGRαCS V of (Y, σ). |
| Example 4.4: Let X= {a, b}, Y= {u, v} and G1 = âßèx, (0.3, 0.3), (0.7, 0.7)âßé, G2 = âßèy, (0.8, 0.7), (0.2, 0.2)âßé. Then τ = {0~, G1, 1~} and σ = {0~, G2, 1~} are IFTs on X and Y respectively. Define a mapping f: (X, τ) → (Y, σ) by f(a) = u and f(b) = v. Then f is an IFWGRα- irresolute mapping. |
| Theorem 4.5: |
| (i) Every IF continuous mappings is an IFWGRα continuous mappings |
| (ii) Every IFα continuous mappings is an IFWGRα continuous mappings |
| (iii) Every IFP continuous mappings is an IFWGRα continuous mappings |
| (iv) Every IFRGα continuous mappings is an IFWGRα continuous mappings |
| (v) Every IFWGRα continuous is an IFRWG continuous |
| Proof: straight forward. |
| Remark 4.6: Converse of the above need not be true. |
| Example 4.7: In Example 4.2, f: (X, τ) → (Y, σ) is an IFWGRα continuous mapping but not an IF continuous mapping. Since G2 = âßèy, (0.8, 0.7), (0.2, 0.2)âßé is an IFOS in Y but f -1(G2) = âßèx, (0.8, 0.7), (0.2, 0.2)âßé is not an IFOS in X. |
| Example 4.8: In Example 4.2, f: (X, τ) → (Y, σ) is an IFWGRα continuous mapping but not an IFα continuous mapping. Since G2 = âßèy, (0.8, 0.7), (0.2, 0.2)âßé is an IFOS in Y but f -1(G2) = âßèx, (0.8, 0.7), (0.2, 0.2)âßé is not an IFαOS in X. |
| Example 4.9: Let X = {a, b}, Y = {u, v} and G1 = âßèx, (0.7, 0.9), (0.3, 0.1)âßé, G2 = âßèy, (0.3, 0.1), (0.7, 0.9)âßé. Then τ = {0~, G1, 1~} and σ = {0~, G2, 1~} are IFTs on X and Y respectively. Define a mapping f: (X, τ) → (Y, σ) by f(a) = u and f(b) = v. Then f is an IFWGRα continuous mapping but not an IFP continuous mapping. Example 4.10: In Example 4.2, f: (X, τ) → (Y, σ) is an IFWGRα continuous mapping but not an IFRGα continuous mapping. Since G2 = âßèy, (0.8, 0.7), (0.2, 0.2)âßé is an IFOS in Y but f -1(G2) = âßèx, (0.8, 0.7), (0.2, 0.2)âßé is not an IFRGαOS in X. |
| Example 4.11: Let X = {a, b}, Y = {u, v} and G1 = âßèx, (0.2, 0.3), (0.5, 0.6)âßé, G2 = âßèy, (0.5, 0.4), (0.4, 0.4)âßé. Then τ = {0~, G1, 1~} and σ = {0~, G2, 1~} are IFTs on X and Y respectively. Define a mapping f: (X, τ) → (Y, σ) by f(a) = u and f(b) = v. Then f is an IFRWG continuous mapping but not an IFWGRα continuous mapping. |
| Theorem 4.12: Let f: (X, τ) → (Y, σ) be a mapping where f -1(V) is an IFRCS in X for every IFCS in Y. Then f is an IFWGRα continuous mapping but not conversely. |
| Proof: Let A be an IFCS in Y. Then f -1(V) is an IFRCS in X. Since every IFRCS is an IFWGRαCS, f -1(V) is an IFWGRαCS in X. Hence f is an IFWGRα continuous mapping. |
| Example 4.13: In Example 4.2, f: (X, τ) → (Y, σ) is an IFWGRα continuous mapping but but not a mapping defined in theorem 4.12. |
| Theorem 4.14: Let f: (X, τ) → (Y, σ) and g: (Y, σ) → (Z, η) be any two maps. Then |
| (i) g âÃËÃË f is IFWGRα continuous, if g is IF continuous and f is IFWGRα continuous |
| (ii) g âÃËÃË f is IFWGRα irresolute, if g is IFWGRα irresolute and f is IFWGRα irresolute |
| (iii) g âÃËÃË f is IFWGRα continuous, if g is IFWGRα continuous and f is IFWGRα irresolute |
| Proof: |
| (i) Let V be any IFCS in (Z, η). Then g-1(V) is an IFCS in (Y, σ), since g is IF continuous. By hypothesis, f-1(g-1(V)) is an IFWGRαCS in (X, τ). Hence g âÃËÃË f is IFWGRα continuous. (ii) Let V be an IFWGRαCS in (Z, η). Since g is IFWGRα irresolute, g-1(V) is IFWGRαCS in (Y, σ). As f is IFWGRα irresolute, f-1(g-1(V)) = (g âÃËÃË f)-1(V) is an IFWGRαCS in (X, τ). Hence g âÃËÃË f is IFWGRα irresolute. (iii) Let V be an IFCS in (Z, η). Since g is IFWGRα continuous,g-1(V) is an IFWGRαCS in (Y, σ). As f is IFWGRα irresolute, f-1(g-1(V)) = (g âÃËÃË f)-1(V) is an IFWGRαCS in (X, τ). Hence g âÃËÃËf is IFWGRα continuous. |
APPLICATIONS OF INTUITIONISTIC FUZZY wgrα-CLOSED SETS |
| In this section we have provide some applications of intuitionistic fuzzy wgrα-closed sets in intuitionistic fuzzy topological spaces. |
| Definition 5.1: A space (X,τ) is called IFwgrα-T1\2 space if every IFWGRαCS is an IFαCS. |
| Definition 5.2: A space (X,τ) is called IFwgr-T1\2 space if every IFWGRαCS is an IFCS. |
| Theorem 5.3: For an IFTS (X, τ) the following conditions are equivalent |
| (i) X is IFwgrα-T1\2 space. |
| (ii) Every singleton of X is either IFRαCS (or) IFαOS. |
| Proof: (i)⇔(ii) Let x ∈ X and assume that {x} is not IFRαCS. Then clearly X−{x} is not IFRαOS and X-{x} is trivially IFWGRαCS. By (i) it is IFαCM and thus {x} is IFαOS. (ii) ⇔ (i) let A ⊂ X be an IFWGRαCS. Let x ∈ cl(int(A)). To show x ∈ A. Case (i) the set {x} is an IFRαCS. Then if x ∉ A, then A ⊆ X-{x}. Since X is IFWGRαCS and X-{x}is an IFRαOS, cl(int(A)) ⊆ X-{x}and hence x ∉ cl(int(A)). This is a contradiction. Therefore, x ∈ A. Case (ii) the set {x} is an IFαOS. Since x ∈ cl(int(A)), then {x} ∩ A ≠ υ implies x ∈ A. In both the cases x ∈ A. This shows that A is an IFαCS. |
| Theorem 5.4: Let (X, τ) be an IFTS and (Y, σ) be an IFwgr-T1\2 space and f: (X, τ) → (Y, σ) be a map. Then the following are equivalent. |
| (i) f is IFWGRα irresolute. |
| (ii) f is IFWGRα continuous. |
| Proof: (i) ⇒ (ii) Let U be an IFCS in (Y, σ). Since f is an IFWGRα irresolute, f-1(U) is an IFWGRαCS in (X, τ). Thus f is IFWGRα continuous. (ii) ⇒ (i) Let F be an IFWGRαCS in (Y, σ). Since Y is an IFwgr-T1\2 space, F is an IFCS in Y. By hypothesis f-1(F) is an IFWGRαCS in X. Therefore f is an IFWGRα irresolute. |
| Theorem 5.5: |
| (i) IFαO(X, τ) ⊂ IFWGRαO(X, τ). |
| (ii) A space is an IFwgrα-T1\2 space if and only if IFαO(X, τ) = IFWGRαO(X, τ). |
| Proof: (i) Let A be an IFαOS. Therefore X−A is an IFαCS. Every IFαCS is an IFWGRαCS. Therefore X−A is an IFWGRαCS, which implies A is an IFWGRαOS. (ii) Let X be an IFwgrα-T1\2 space. Let A ∈ IFWGRαO(X, τ), X – A is an IFWGRαCS implies X−A is IFαCS. Hence A ∈ IFαO(X, τ). Therefore IFWGRαO(X, τ) ⊂ IFαO(X, τ) and IFαO(X, τ) ⊆ IFWGRαO(X, τ). Which implies IFαO(X, τ) = IFWGRαO(X, τ). Conversely, let IFαO(X, τ) = IFWGRαO(X, τ). A is IFWGRαCS implies X−A is an IFWGRαOS. By assumption X−A is an IFαOS and hence A is IFαCS. |
| Theorem 5.6: Let (Y, σ) be an IFwgr-T1\2 space, f: (X, τ) → (Y, σ) and g: (Y, σ) → (Z, η) be two IFWGRα continuous functions, then g âÃËÃË f: (X,τ) → (Z,η) is also an IFWGRα continuous. |
| Proof: Let V be any IFCS in (Z, η). Since g-1(V) is IFWGRαCS in (Y, σ). IFWGRα continuity of f implies that f-1(g-1(V)) = (g âÃËÃË f)-1(V) is an IFWGRαCS. Hence (g âÃËÃË f) is an IFWGRα continuous. |
References |
|