E- ISSN: 2320 - 3528
P- ISSN: 2347 - 2286
E- ISSN: 2320 - 3528
P- ISSN: 2347 - 2286
Jacques THIERIE*
Free University of Brussels, Brussels, Belgium
Received date: 19 June 2015; Accepted date: 07 September 2015; Published date: 10 September 2015
Visit for more related articles at Research & Reviews: Journal of Microbiology and Biotechnology
Analysis of the Luedeking-Piret model during the oxidative respiration to respirofermentative transition in a consortium grown in a chemostat revealed a significant increase in a parameter (β) of the Luedeking-Piret model in butyrate production. These data implied the possibility of improved capacity for cellular metabolites production under some culture conditions. Additionally, the parameter β was positively associated with a dilution rate above the critical dilution rate, suggesting the potential for enhancing industrial processes production using prokaryotes.
Luedeking-Piret model, Respirofermentative transition, Bacterial consortium, Secondary metabolites
The Luedeking–Piret is an empirical relationship widely used to evaluate specific production rates of some metabolites or other products in cultured cell. It was initially developed in 1959 for lactic acid production in batch and continuous culture; next it was applied to numerous other types of production, as much to prokaryotes as to eukaryotes.
On the other hand, in natural (or semi-natural) environments, the great majority of microorganisms, (especially bacteria) live in aggregates, biofilms, or flocs.
In this work, we couple the interesting features a floc cultivation (stability, extensive metabolic properties, etc.) with the production of butyric acid; we show that, under certain conditions, the parameters of the Luedeking-Piret model cease to be constant and can then be used to increase culture performance.
In a recent study [1], we have shown how a specific interpretation of the manifold domains allowed us to highlight changes (positive or negative) in the empirical parameters of the Luedeking-Piret model
![]() (1)
(1)
Where B is a product, X is the total biomass and α, β are empirical parameters. This model successfully accounts for the production rate of B by cell culture X.
Generally, the two parameters are constants and characterize the culture.
In this work, α and/or β were shown to potentially depend on external conditions (such as the chemostat dilution rate, for example).
Material and methods have been extensively described in ref. [2] and in ref. [3]. We only mention little useful information.
An activated sludge sample was harvested in an activated sludge wastewater treatment plant (Erasme University Medical Center, Brussels) and cultivated in a synthetic sewage feed (SSF) [4] enriched with 0.5% glucose (wt/vol). The bioreactor walls were thoroughly and regularly cleaned to prevent the biofilm growth.
A bacterial floc forming consortium developed the in continuous culture and was stable over many years. Unexpectedly, it was able to exhibit a Crabtree-like effect. Figure 1 depicts the main components (biomass substrate and lactic acid) produced in the chemostat; these components matched the characteristic profiles of the Crabtree effect (similar to that observed in S. cerevisiae, for example). A critical value around Dc=0.25 h-1 characterized the respiratory transition. However, variations in lactic acid as a function of D are complex and a sophisticated mathematical model is required to account for this phenomenon [5]. (The model is beyond the scope of the present paper.)
Figure 1: Main state variables versus dilution rate. Evolution of the total biomass (X), glucose (GLU) and lactic acid (Lac) produced in the chemostat as a function of the dilution rate. The oxidative respiration to respirofermention transition occurred near D=0.25 h-1. The curves are discontinuous and the lactic acid concentration passes through a maximum. (Symbols: experimental data; solid lines: fittings).
Figure 2 shows a very simple curve, demonstrating the change in butyric acid concentration versus D. In contrast to the profile observed for lactic acid, the butyrate curve was continuous and no critical value was observed during the oxidative to respirofermentative transition. This behaviour required special cell production qualities as is examined herein.
The Model: Researchers have recently aimed to understand the production and metabolism of butyrate, both for industrial reasons [6,7] and because of its role in gut physiology [8,9].
Figure 2: Butyrate concentration versus dilution rate. The butyrate concentration yielded a simple continuous (decreasing) curve. The profile was inversely proportional to the dilution rate, and has no critical value for this metabolism. We believe this result was due to physiologic adaptation in butyrate-producing cells after the respirofermentative transition. (Symbols: experimental data; solid lines: fittings).
As it has been said, the consortium that was cultivated in this study was harvested from a municipal wastewater treatment plant sludge; it was therefore not surprising to find intestinal anaerobic bacteria producing butyrate as a fermentation product [8,9]. The consortium contained at least 11 bacterial species, including aerobic, anaerobic and mixed bacteria. Polymerase chain reaction (PCR) analysis showed that only bacterial genetic material was present in the culture. The specific butyrate-producing species has not yet been identified; however, for the sake of simplicity, the following two assumptions were adopted:
1. A single bacterial species (or a homogeneous group) produces butyrate.
2. The competition between butyrate-producing and non-producing species is low enough to be negligible as a first approximation. We have moreover shown that anaerobic species within a floc are relatively isolated [10].
Now, consider a chemostat and three state variables: X, the total biomass; B, a metabolic product; and C, cells producing the metabolic product B. These three variables can be represented by a system of differential equations, according to the mass balance
![]() (2)
(2)
Where μX is specific growth rate of the biomass.
![]() (3)
(3)
and μC is the specific growth rate of the producing cells.
The implicit mass balance for the product of B is
![]() (4)
(4)
Where ΠB is the production rate of B by C.
In the nontrivial steady state (non-zero variables), ![]() , implying that all specific cellular growth rates are equal to D. The steady state of (4) is
, implying that all specific cellular growth rates are equal to D. The steady state of (4) is
![]() (5a)
(5a)
Or
![]() (5b)
(5b)
General. The lactic acid production.
We used the results of the general two pathways model widely described in [5] to interpret the results appearing in Figures 1 and 2. Surprisingly, the same model also applies to explain the Crabtree effect in Saccharomyces cerevisiae [5]. Full development of the calculation is a bit long and may not be providing essential information for the butyrate production.
In short, the model uses two transport/metabolization pathways (T/M) to explain the Crabtree effect.
A high affinity (h) T/M is given by ![]() and a low (l) affinity T/M is expressed as
and a low (l) affinity T/M is expressed as ![]()
A simplified formalism is as follow: S represents the substrate; P the product (lactic acid); qz is the specific production rate of z; KS is the affinity for the substrate; VS is the maximum T/M transport rate; X is the biomass.
The mass concentration of a product P is calculable by ![]() where qp = gs(vi).(1-β).qs(1); β is a constant correlated to the product excretion; gs(vi) is a constant depending of the stoichiometry of the transformation of the substrate in the product:
where qp = gs(vi).(1-β).qs(1); β is a constant correlated to the product excretion; gs(vi) is a constant depending of the stoichiometry of the transformation of the substrate in the product: ![]() As the SSF is a complex substrate, it was necessary to express it in glucose equivalent.
As the SSF is a complex substrate, it was necessary to express it in glucose equivalent.
The above reasoning clearly shows that the production of lactic acid is complex and depends mainly on a portion of the T/M branch at low affinity for the substrate ![]() .
.
b) The butyric acid production.
The production of butyric acid appears, on the contrary, much easier to represent.
By examining Figure 2, it was assumed that ΠB=constant could be a good fit for the function B=f (D). This fitting is effectively acceptable and yields ΠB=0.012 ± 0.001 g/(L h); r2=0.93.
This hypothesis was confirmed by using Equation 5a and experimental values (Table 1).
The mean value was ΠB=0.016 ± 0.001 g/(L.h). The butyrate production rate in this consortium was then a constant of approximately 0.015 g/(L.h).
Thus, the Luedeking-Piret model (Equation 1), could be rewritten as
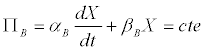 (7)
(7)
In the case of butyrate, one has that [11]
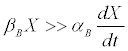 (8)
(8)
This is usually the rule for a fermentation end product, which is frequently how butyrate may be viewed. In the case of a by-product [12], αB=0 [13] and (Equation 8) is absolutely verified. (Furthermore, butyrate may also form building blocks for various by-products [14-16], which improves the validity of (8)).
Using (Equation 8) in (Equation 7), and assuming that B=BUT, it is possible to calculate
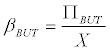 (9)
(9)
Which is equivalent to the specific production rate butyrate (in h-1).
This relationship is depicted in Figure 3.
Figure 3: Behavior of the second parameter of the Luedeking-Piret model versus dilution rate. βBUT (equivalent to the specific production rate (SPR) of butyrate) had a constant value (0.022 h-1) below the critical transition respirofermentative value (DC) but was linearly dependent on the dilution rate beyond DC. Around the maximum value of D (washout), the SPR was about 10 times greater (0.2 h-1) than that below DC. This could be explained by the mechanism through which the producing anaerobic cells metabolically adapt to butyrate production during the respirofermentative transition of the consortium. (Δ) βBUT = cte=0.0217 ± .0008 h-1; (O) 0 ; β0BUT = β0BUT + aD 0 β0BUT = -0.086 ± 0.014 h-1 and a=0.480 ± 0.003 (r²=0.99). (Symbols: experimental data; solid lines: fittings).
Two regions clearly appear. Below the respirofermentative critical value, βBUT is a constant equal to 0.023 ± 0.001 h-1; however, above the critical value, βBUT ceases to be constant and linearly depends on D:
![]() (10)
(10)
With ![]() -0.086 ± 0.014 h-1 and a=0.480 ± 0.003 (r2=0.99).
-0.086 ± 0.014 h-1 and a=0.480 ± 0.003 (r2=0.99).
Near the washout (D ≈ 0.6 h-1) βBUT is close to 0.2 h-1, 10 times the purely oxidative respiratory mode.
This work revealed an increase in the specific butyrate production rate, which is of paramount importance for the industrial or commercial application of this metabolite (as well as other). Butyric acid is fairly easy to convert into butanol. The challenge is still greater when considering the biofuel aspect of the process bringing by butanol. Ramey and Yang [7] describe in great detail the challenges of this transformation in the final report of the US Department of Energy. Our approach does not require anaerobic conditions or sterility for the production of butyric acid as in the business plan and opens new interesting economic perspectives, whereas we produce this intermediate from wastewater treatment plants ... and not corn!
In the example described herein, the use of a single chemostat did not provide the ideal conditions (low yield, poor selectivity, and substrate spilling). Therefore to take advantage of the results of our study, an appropriate bioreactor is needed. Merely by way of illustration, Du et al. [6] described a continuous culture utilizing partial cell recirculation that exhibited selectivity and a productivity of around 1.13 g/(L.h). They used a pure strain and worked at low dilution rates. In addition, they did not take precautions to ensure that (Eq. 8) was satisfied (e.g., by inhibiting the cell growth rate). Our technique provides a suitable mode for improvement of butyrate production. However, we believe that our work also reveals a novel method for increasing the production of secondary metabolites using metabolic engineering under favourable growth conditions.
As a final comment, we wish to emphasize that the consortium described herein was made of flocs. Bacteria are embedded in small “mucus” structures (the extracellular polymeric substances or EPS; [17]. The flocs are in suspension in the matrix phase of the chemostat. This situation is different from a fixed-culture (on a solid medium or when forming a biofilm). Unlike consortia formed of independent cells put together [18], the bacterial floc doesn’t pose any dynamic stability problem encountered with single cells [19,20]. Moreover, the emergent properties of the flocs are sometimes larger to those of isolated cells. Here, we have seen that simultaneous growth of 11 species, reaches a washout value close to 0.8 h-1, which is a high value for anaerobic bacteria. As noted earlier [10], the coordinated development of a floc is not easily seen. This phenomenon deserves to be studied to allow building specific flocs usable for the production of particular compounds.