ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
S.V.R.Arun1, S.Porselvi2, DR.A.N.Balaji3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Scheduling problems have played a vital role in recent years due to the fast growing of consumer demand for variety,quality, reduced product life cycles, competing with global competition and rapid development of new technologies. The Flow Shop Scheduling Problem (FSP) is one of the most popular scheduling models existing in practice, which is among the hardest combinatorial optimization problems . Particle Swarm Optimization (PSO) is a population based metaheuristic that takes advantage of indvidual and social cooperation in a Swarm. It has been applied to variety of optimization problems because of its simplicity and fast convergence. In this paper PSO is presented to solve the flowshop sequencing problem with an objective of minimizing the Total weighted delay of jobs. For this purpose a heuristic rule called the smallest position value(SPV) is used to enable the continous PSO to be applied in sequencing problems.
Keywords |
| Particle Swarm Optimization , Shortest position value rule, Total weighted delay |
INTRODUCTION |
| Metaheuristics are general frameworks commonly used for solving hard optimization problems. To examine a search space systematically, they employ intelligent and powerful heuristic mechanisms for both exploration and exploitation ([2] Mostafa Akhshabi, Javad Haddadnia). Amongst several metaheuristics using various search philosophies, ones providing dynamic balance between exploration and exploitation, usually deliver better performance. If exploration is the governing feature of a metaheuristic, it may perform a vague examination on the search space and generally misses good solutions. On the contrary, if exploitation is dominant, the entire search space may not be explored and premature convergence to a local optimum is possible Particle Swarm Optimization (PSO) is a metaheuristic introduced by Kennedy and Eberhart . |
| PSO is inspired of the behaviors of social models like bird flocking or fish schooling and is based on individual improvement and social cooperation [J. Jerald · P. Asokan [4]]. In PSO, a population of particles (swarm) flies over a multidimensional search space representing candidate solutions. During their search journey determined by their current tendency, personal experience and swarm’s experience, particles are expected to explore the whole search space and to tend towards the optimal solution PSO is initially proposed for continuous nonlinear optimization problems ([8] Ken Van den Enden2 and Thomas St¨utzle). Later it becomes quite popular and is applied to a wide range of optimization problems due to rapid swarm convergence and simplicity in its conceptual features and implementation . Although rapid convergence is a desirable advantage, it may result in a severe premature convergence problem, as well . The swarm may converge to a local solution and may not escape from it to explore the search space thoroughly. Moreover, PSO has a shortcoming in finding the best solution around a local neighborhood . Several modifications on the standard PSO algorithm are proposed to rectify above mentioned drawbacks. Most of these modifications concern only on either exploration or exploitation mechanism and merely correct the deficiencies partially. They locate good solutions for some of the problem types but fail to produce competitive results for others. For instance, while the methods concentrated on exploration mechanism improve the solution quality for multimodal continuous function optimization problems, they typically generate inferior solutions for unimodal problems. In this paper, a PSO algorithm with improved exploration and exploitation mechanisms is proposed. In PSO, the general flow of the PSO algorithm is preserved. However, among the PSO iterations, the search strategy is temporarily modified only for the particle(thepioneering-particle) which achieves or enhances the best solution. For the pioneering-particles, Shortest position value(SPV) is employed. The solutions obtained by SPV do not affect swarm’s experience in order to find promising search areas afterwards and not to hinder exploration. To improve exploration further and to prevent premature convergence, the pioneering-particles continue their search journey with random velocities and their previous experience. The primary advantage of PSO is its applicability to many different types of optimization problems with satisfactory performance. To support this claim, we experimented PSO on both continuous and discrete problems. Results for the continuous problems indicate that our approach improves the search capability of the standard PSO algorithm. PSO produces comparable solutions for both unimodal and multimodal functions while other similar PSO variants deliver poor solutions for either unimodal or multimodal functions. Moreover, our approach achieves the best known solutions for almost all instances of the Orienteering Problem (OP) which is a discrete NP-hard problem.Besides proposing a promising and valuable tool for solving different types of problems (continuous or discrete / unimodal or multimodal) satisfactorily, there are two auxiliary contributions of this paper; Firstly,we present the first successful PSO based algorithm for OP . IS-PSO which is derived from PSO,reproduces the best known solutions for all benchmark problems. Secondly, we propose that SPV with dynamic neighborhoods is a good alternative for a subsidiary local search([5] M.Faith Tasgetiren et al). |
PARTICLE SWARM OPTIMIZATION |
| Particle Swarm Optimization (PSO) is a population-based method in which a swarm includes n individuals called particles. Each particle has a d-dimensional position vector representing a candidate solution and a ddimensional velocity vector expressing the current tendency of the particle during its search journey. Initial swarm can be constructed randomly or by using some predetermined values. At each step, the velocity of each particle is re-evaluated based on the particle’s inertia as well as the social interaction (swarm’s experience) and personal experience of the particle. The experience of each particle is usually captured by its local best position(pbest ). The experience of the swarm is captured by the global best position (gbest ). In the course of several iterations, particles make use of this experience and are supposed to move towards the optimum position. |
| PSEUDO CODE |
| Procedure of PSO |
| Initialize parameters |
| Initialize population |
| For each particle |
| Evaluate |
| Update Local best |
| Update global best |
| Update velocity and position |
| While(not terminated) |
| End procedure |
| Pseudo-code of the standard PSO algorithm is illustrated above. Optimization is achieved in the course of several iterations of update-evaluate steps. During the update step at iteration t, the velocity and the position vector of each particle are calculated by using equations . In these equations are the velocity and the position values of the jth dimension (1 ≤ j ≤ d) of the ith particle (1 ≤ i ≤ n) at iteration . The stochastic behavior of PSO is achieved by random numbers rand 1 and rand 2 which are positive numbers generally uniformly distributedin [0, 1]. |
| After the update step, the fitness function value is calculated for each particle based on its position (the candidate solution represented by the particle.) The local best position, pbest of each particle and the global best position, gbest of the swarm are updated if the candidate solution is better than gbest is considered as the best solution.PSO algorithm for FSP The gbest model of kennedy et al.is followed in this study.according to the gbest model,each particle moves towards its best previous position and towards the best particle moves towards the best particle in the whole swarm.In the PSO alogorithm for fsp,parameters were initialized and the initial population was generated randomly since evaluation of each particle in the swarm requires the determination of the permutations of the job for fsp, the smallest position value(SPV) rule applies to each particle corresponding permutation thus each particle will be evaluated by using the permutation to compute the fitness function value.the objective function for the fsp with total weighted delay.after evaluation ,the PSO algorithm repeats the following steps iteratively. With its position,velocity,and fitness value,each particle updates its personal best (best value of each individual so far) if an improved fitness value was found.on the other hand the best particle in the whole swarm with its fitness and position was used to update the global best. Then the velocity of the particle is updated by using its previous velocity,the experiences of the personal best,and global best in order to determine the position of each particle. The permutation is determined through the SPV rule so that evaluation is again performed to compute the fitness of the particles in the swarm .this process is terminated with a pre-determined stopping criterion. |
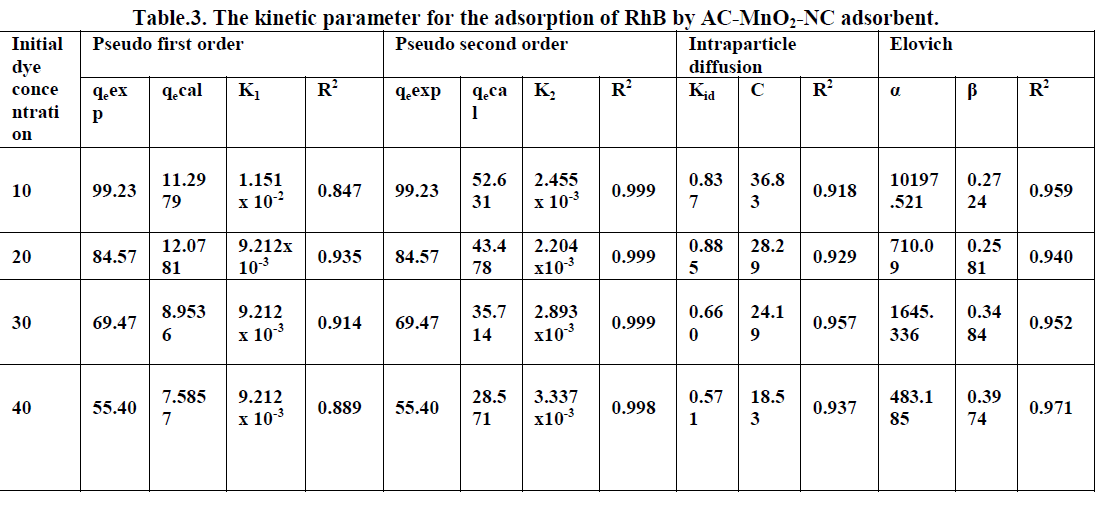 |
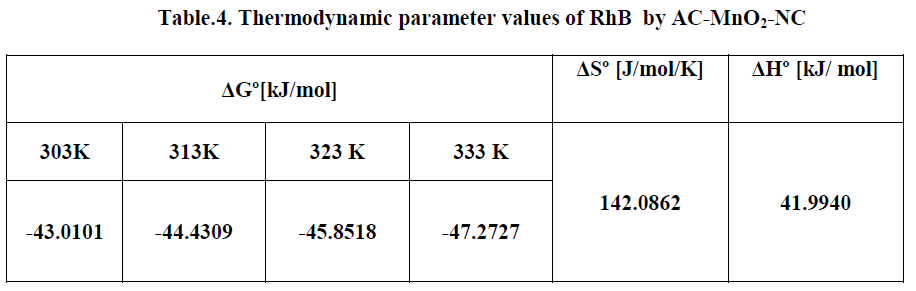 ' ' |
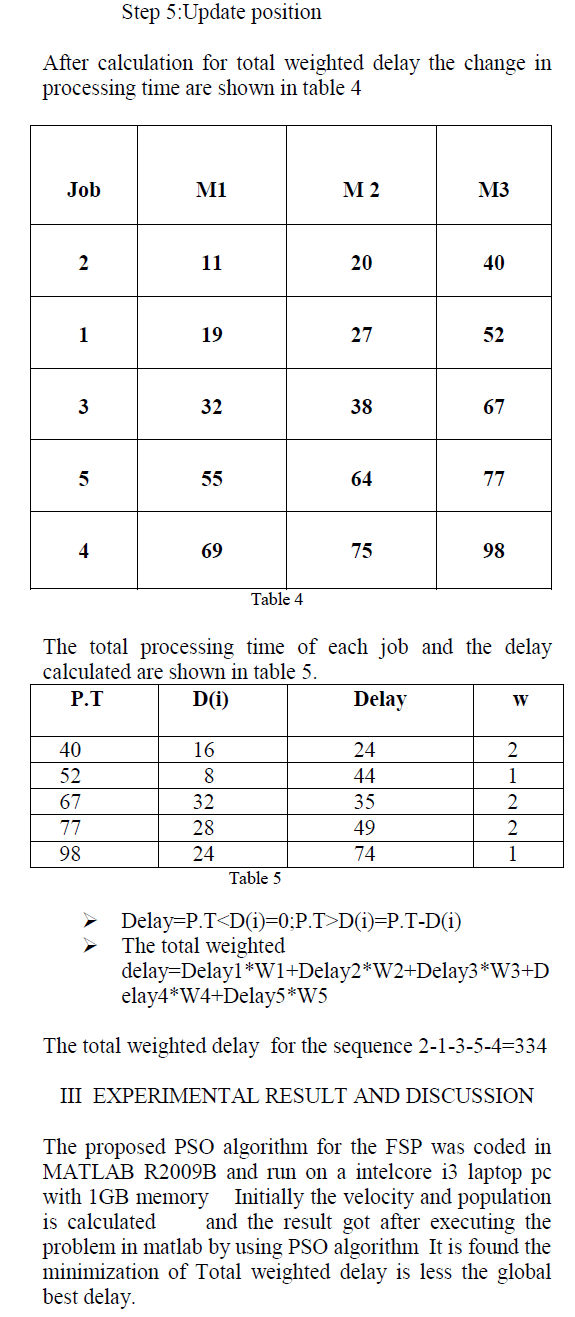 |
| The personsal best delay got is in sequence 3-2-4-5- 1=250 |
CONCLUSION |
| To the best of my knowledge ,this is the first reported application of the particle swarm optimization algorithm to solve the FSP with total weighted delay of jobs in the literature. Here SPV rule is used to enable the continuous PSO algorithm to be applied to all classes of sequencing problems.and the result got is better than the global best solution |
References |
|