Mixed Convection Stagnation Point Flow of
Casson Fluid with Convective Boundary
Conditions

G. Mahanta S. Shaw

Mixed Convection Stagnation Point Flow of Casson Fluid with Convective Boundary Conditions

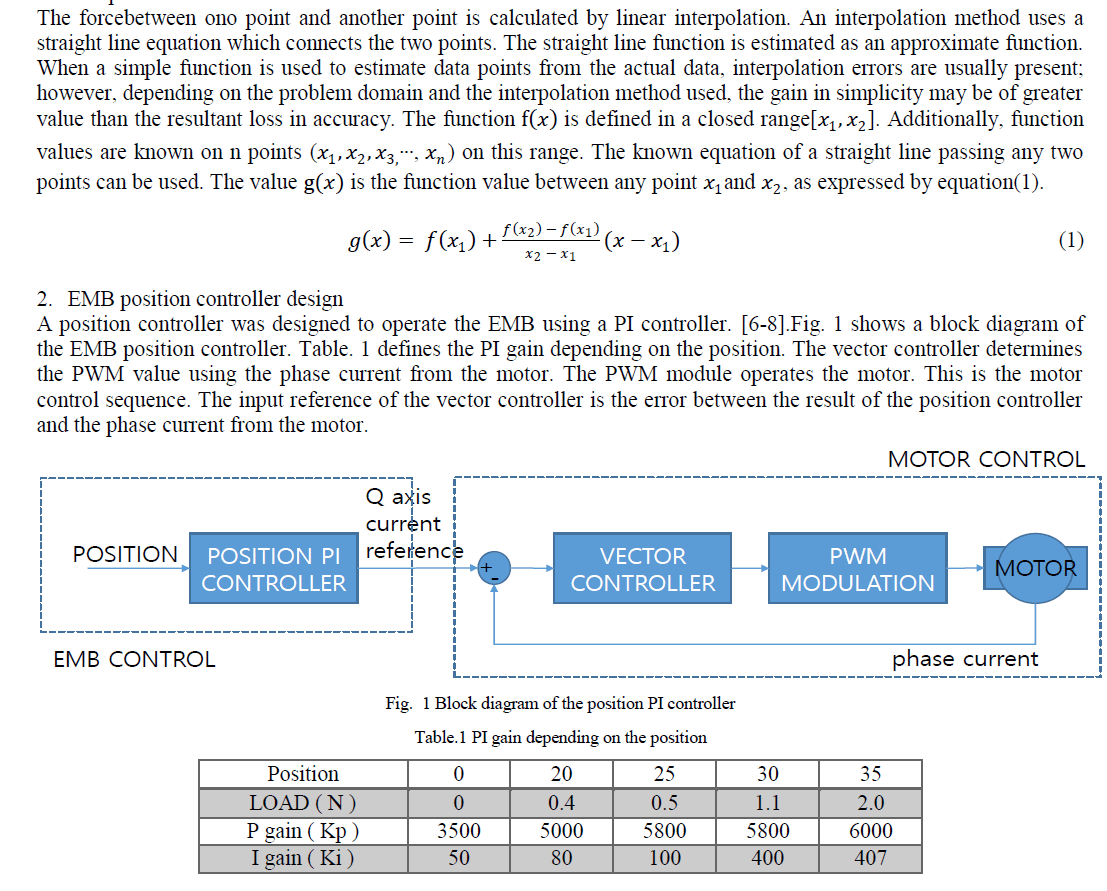
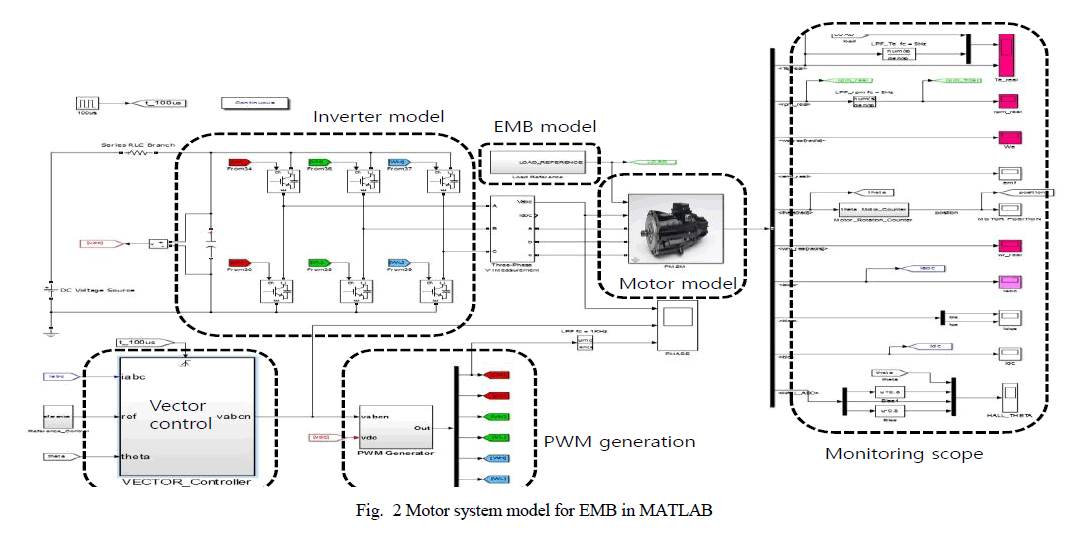
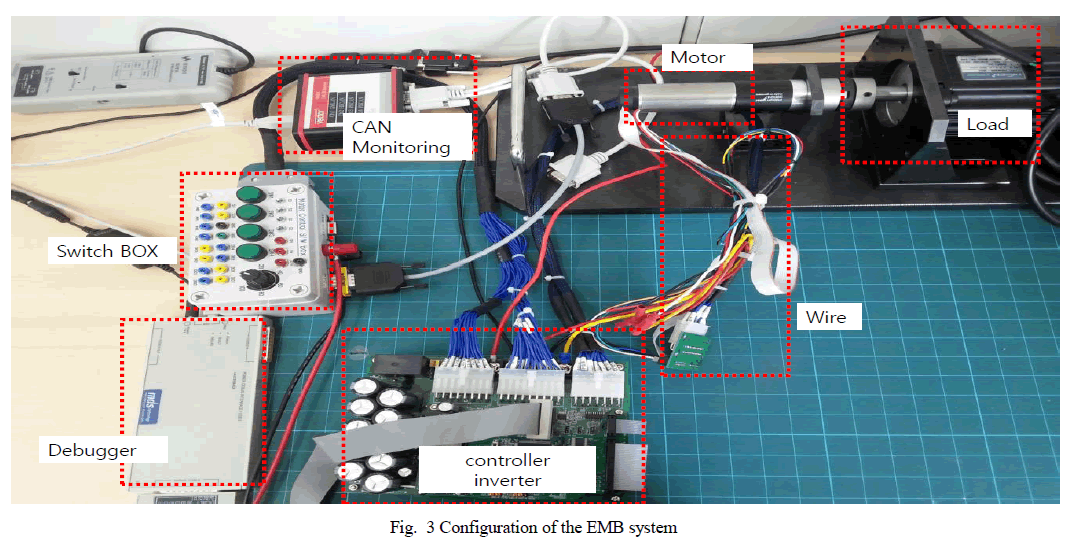
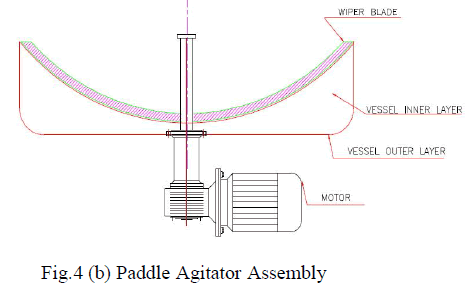
G. Mahanta S. Shaw
Department of Mathematics, Kalinga Institute of Industrial Technology, Bhubaneswar, Odisha, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Casson fluid flow has many practical applications food processing, metallurgy, drilling operations and bio-engineering operations. In the present paper we investigate the mixed convection stagnation-point flow of an incompressible non-Newtonian fluid over a stretching sheet with magnetic field under convective boundary condition. The resulting partial differential equations are converted into the ordinary differential equations by the suitable transformations. The velocity, temperature and concentration profiles are computed by employing the homotopy analysis method. The plotted graphs illustrate the flow and heat transfer characteristics and their dependence upon the embedded parameters. Numerical values of skin-friction coefficient, Nusselt number and Sherwood number are given and examined. Comparison of the present results with the existing solution is also given.

Keywords

Casson fluid, Magnetic field, convective boundary condition, Stagnation point.

INTRODUCTION

The stagnation point flow and heat transfer over a stretching sheet are commonly seen in paper production, the spinning of fibers, glass blowing, continuous casting, manufacture of sheeting material through extrusion process especially in the polymer extrusion in a melt spinning process, aerodynamic extrusion of plastic sheets etc. Chiam[1] studied a twodimensional stagnation point flow of viscous fluid towards a linear stretching surface. Mahapatra and Gupta[2] analyzed the heat transfer in the stagnation point flow towards a stretching surface. The steady stagnation point flow of an incompressible micropolar fluid over a stretching surface is addressed by Nazar et al.[3] The stagnation point flow of an upper convected Maxwell fluid has been numerically reported by Sadeghy et al.[4] The mixed convection stagnation point flow of an incompressible viscous fluid towards a vertical permeable stretching sheet is studied by Ishak et al.[5] .The effect of radiation on the mixed convection MHD stagnation point flow in a porous space is examined by Hayat et al.[6] Mahapatra et al.[7] carried out the analysis for the steady two-dimensional oblique stagnation point flow of an incompressible viscoelastic fluid towards a stretching sheet.Groson et.al.[8]carried outtheanalysis Magnetohydrodynamic oblique stagnation-point flow

Robert et.al. carried out the analysisHydromagnetic stagnation point flow of a viscous fluid over a stretching or shrinking sheet[9] Lok et.al[10] analysis Mixed convection flow of a micropolar fluid near a non-orthogonal stagnation-point on a stretching vertical sheet.Ali et.al.[11] carried out the analysis MHD stagnation point flow and heat transfer towards stretching sheet with induced magnetic field. Ming et al.[12] presented the fractal analysis of Casson fluid flow through porous space. Attia, [13] carried out the analysis, Hydromagnetic stagnation point flow with heat transfer over a permeable surface. Garg[14] carried out the analysis, Heat transfer due to stagnation point flow of a non-newtonian fluid. Nakayama et.al.[15]studied the analysis of, Free convection heat transfer over a non-isothermal body of arbitrary shape embedded in a fluid saturated porous media.. Hassanien, et.al[16] Effect of thermal dispersion and stratification on non-darcy mixed convection from a vertical plate in a porous medium.Dutta et.al[17] studied the, Temperature field in the flow over a stretching surface with uniform heat flux. Chiam[18] carried out the analysis,the Stagnation point flow towards a stretching plate.

MATHEMATICAL FORMULATION

CONCLUSION

The nonlinear problem of stagnation point flow of Casson fluid over a stretching surface subject to convective boundary conditions with magnetic field. The main points of the present study are listed as follows:

1. The velocity and temperature profiles decrease when the non-Newtonian Casson parameter increases β and the concentration profiles increases.

2. There is a prominent increase in the velocity and boundary layer thickness when λ1 increases. However, the temperature and concentration profile decreases by increasing λ1.

3. An increase in the Prandtl number also corresponds to the weaker thermal diffusivity which therefore reduces the thermal boundary layer thickness.

4. An increase the Eckert number thermal boundary thickness increases. Whereas the concentration and the momentum boundary layer thickness decreases with increase of Eckert number.

5. The temperature field as well as concentration increases with the increase of magnetic field.

6. The influence of the Biot number Bi on velocity and temperature profiles are qualitatively similar.

7. The velocityf" (n) is an increasing function of a/c. An increase in a/c decreases the dimensionless temperature and concentration profile.

References

Chiam T C two-dimensional stagnation point flow of viscous fluid towards a linear stretching surface. J. Phys. Soc. Jpn. 63 2443, 1994 .
Mahapatra T R and Gupta A S the heat transfer in the stagnation point flow towards a stretching surface. Heat Mass Transfer38 517 ,2002.
Nazar Ra, Amin Na, Diana Filipb, Pop I, . The steady stagnation point flow of an incompressible micropolar fluid over a stretching surface is addressed. Int. J. Non-Linear Mech. 39 122 ,2004.
Kayvan Sadeghya, , , Hadi Hajibeygib, , Seyed-Mohammad TaghaviThe stagnation point flow of an upper convected Maxwell fluid has been numerically reported by Sadeghy Int. J. Non-Linear Mech. 41 1242,2006.
Ishak .A . Nazar R · Pop I. Mixed convection boundary layers in the stagnation-point flow toward a stretching vertical sheet , Malaysian J. Math. Sci. 1 217 ,2007.
Hayata.T, . Abbas Z, , , Pop I., Asghar S The effect of radiation on the mixed convection MHD stagnation point flow in a porous space Int. J. Heat Mass Transfer 53 466,2010.
Ray Mahapatra,.T , Gupta A.S. Heat transfer in oblique stagnation-point flow of an incompressible viscous fluid towards a stretching surface Heat and Mass Transfer , 43(8):767-773,2007,2007.
Grosan T, . Pop I., . Revnic C, Ingham D.B , Magneto hydrodynamic oblique stagnation-point flow, Meccanica 10/2009; 44(5):565-572,2009.
Robert .A. Van Gorder, K. Vajravelu, . Pop I, : Hydromagnetic stagnation point flow of a viscous fluid over a stretching or shrinking sheet, Meccanica (Impact Factor: 1.82). 01/2012; 47(1):31-50.
Lok,Y.Y Pop I., . Ingham B.T, . Amin.T , Mixed convection flow of a micropolar fluid near a non-orthogonal stagnation-point on a stretching vertical sheet, International Journal of Numerical Methods for Heat and Fluid Flow 05/2009; 19(3-4):459-483,2009..
Ali F.M, .Nazar R, .Arifin N.M, Pop I, analysis MHD stagnation point flow and heat transfer towards stretching sheet with induced magnetic field. Applied Mathematics and Mechanics,32(4),409,418,2011.
Attia H.A, Hydromagnetic stagnation point flow with heat transfer over a permeable surface, Arab. J. Sci. Eng. 28 (2003) 107–112.
Garg V.K, Heat transfer due to stagnation point flow of a non-newtonian fluid, Acta. Mech. 104 , 159–171,1994.
Nakayama A, Koyama H, Free convection heat transfer over a non-isothermal body of arbitrary shape embedded in a fluid saturated porous media, ASME J. Heat Transfer 109 , 125–130,1987
Hassanien I.A,. Bakier A.Y, R.S.R. Gorla, Effect of thermal dispersion and stratification on non-darcy mixed convection from a vertical plate in a porous medium, Heat Mass Transfer 34 , 209–212,1998.
Dutta B.K, Roy P, . Gupta A.S, Temperature field in the flow over a stretching surface with uniform heat flux, Int. Comm. Heat Mass Transfer 12 , 89–10,1985.
Chiam T.C, Stagnation point flow towards a stretching plate, J. Phys. Soc. Jpn. 63 , 2443–2444,1985.