ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| D.Esther Kalpana Rani Assistant Professor, Department of Physics, JNTUH College of Engineering, Karimnagar, Andhra Pradesh, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Polarisation effects of multiple scattering of gamma transport can be studied using only the Vector Boltzmann transport equation. The scalar Boltzmann transport equation is utilized when the radiation’s polarisation effects are not taken into consideration. In this article a Monte Carlo code MCSHAPE is used to explain the importance of Vector Model to Scalar Model, using the sources of radiation which produces double scattering peak. The intensity of the double scattering peak of the Vector Model is compared with the Scalar Model which is explained unambiguously
Keywords |
| Scalar and Vector Boltzmann Transport Equation, MCSHAPE, Multiple Scattering, Double scattering peak. |
INTRODUCTION |
| Compton imagined that photons striking the electrons in the target material behaved like other “classical” objects colliding with each other. In this assumption, an incoming photon of a certain energy and momentum would glance off a stationary electron and send the electron recoiling at an angle away from the incident angle of the approaching photon. In these scattering experiments, it was noticed that the scattered X-rays were more readily absorbed than the incident X-rays from the same source (Tipler.et.al, 1999). These results were mostly apparent with high energy X-rays (about 0.1 Mev and above) and meant that the absorbed X-ray photons had less energy than the photons emitted from the source (Dumond 1930). Compton was then able to apply the laws of energy and momentum conservation to derive an equation for the change in wavelength of the scattered photon (Tipler.et.al, 1990). The first analytical approach to the multiple scattering of the Compton Effect was introduced by Dumond in 1930. He predicted that multiple scattering may affect the breadth of the Single Compton line, change its structure and distort the background until rendering unreliable the Compton shift measurements (Dumond 1930). A particular source is chosen so that the radiation has enough energy to penetrate through the material but with sufficiently reduced attenuation when passing through the defect. The increased transmission through a flaw results in a darker image on the developed film. The activity of the source is a critical characteristic since the quality of measurement is affected by it. Too high of an activity adds fog to the film, darkening it overall and reducing the likelihood of identifying the flaw. Techniques using the multiple scattering of X-rays and γ- rays are applied to obtain the information on electron momentum distributions in a wide range of materials (B.G. Williams 1977, M.J. Cooper, 1985 and W. Schulke, 1989). Tanner and Epstein, 1976 examined the general case with the Monte Carlo Technique to determine qualitatively the effects of the sample geometry, the scattering angles, the absorption coefficients and the shape of the scattering cross- sections on the intensities of single and higher order scattering. They described the energy profile reflected by a cylindrical sample as much of finite as of infinite radii of infinite thickness and assuming constant absorption coefficients. However, a detailed analytical solution with recourse either to the scalar transport equation (Fernandez, 1991; Fernandez and Sumini 1992) or to the vector transport equation (Fernandez, 1993a) is possible as has been demonstrated. In the present study three radioactive sources are taken and multiple scattering chains were studied with respect to the scalar model as well as the vector model and a comparative explanation is made. |
II. THEORY |
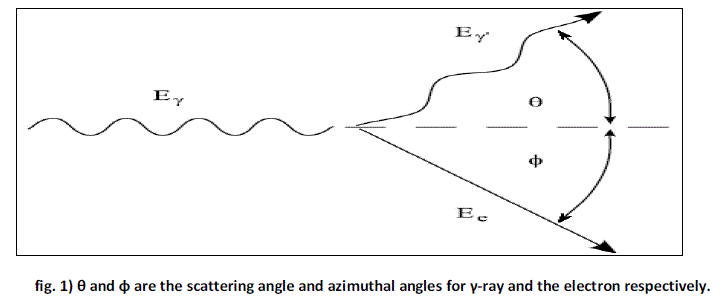
| In fig. 1 a gamma ray of energy Eθ scatters from an electron (for convenience all energies are expressed in Mev). The law of conservation of energy and momentum for the interaction are as follows: |
 |
 |
| Multiple collisions will mix the effects of the polarization on the single participating collisions. In this way multiple collisions involving the photoelectric effect proceeded by a scattering collisions will bring the effect of polarization also on the characteristic lines. Under these circumstances, there is no one part of the X-ray spectrum that remains completely independent of the state of polarization of the source. This is another reason to describe in detail about the state of polarization of the photons at each interaction (J.E. Fernandez, 1991). |
2.1 Chains of double scattering involving the Rayleigh and Compton effects using the Scalar Transport Equation and also the Vector Transport Equation: |
| There are four contributions involving a double scattering with the Rayleigh and the Compton effects Rayleigh-Rayleigh, Compton-Compton, Compton-Rayleigh and Rayleigh-Compton. The mathematical complexity in the computation of these intensities depends on whether the involved scattering is Rayleigh or Compton. The Rayleigh scattering contributions are discrete and do not change the energy of the incident radiation. The intensities contributed by the Compton Effect depend on the coupled relationship between the scattering angle cosine and the wavelength shift which introduces some difficulties in the computations of these processes. The details of the equations related to those double scattering and their computations for scalar model as well as vector model are described elsewhere in (J.E.Fernandez et.al., 1991). Many authors attempted an analytical description of the multiple scattering spectrum using three approaches: the calculation of the scattered electric field (Dumond 1930; Williams. et.al., 1974), the integration of a probabilistic differential intensity (Tanner and Epstein 1976a, 1976b; Braun- Keller and Epstein 1977a, 1977b) and the Boltzmann Transport Equation rather than single terms of multiple scattering. Some leading authors in this field considered for this reason that transport theory is unable to separate the multiple order contributions (Halonen.et.al, 1977). Since the mentioned analytical descriptions were insufficient to correct for the Compton profiles (Cooper, 1985; Halonen.et.al, 1977), the spectral distribution of multiple events was calculated with Monte Carlo Simulation (Felsteiner.et.al., 1974; Felsteiner and Pattison, 1975; Pitkanen et.al, 1986). |
2.2 Radioactive Sources |
| Radioactive sources are used for diagnosis, treatment and research. For example doctors find certain diseases by injecting a radioactive source and monitoring the radiation given off as the substance moves through the body (Nuclear Medicine-Wikipedia Article). Radioactive Source contains a quantity of radioactive material permanently sealed in a capsule or closely bonded in an inert substance which can be used under normal usage. Some of the radioactive sources which are also gamma sources are Cesium 137, Americium 241 and Cerium 141. Cesium 137: In practice, the use of Cs137 source emitting the mono-energetic gamma rays of 661 kev is known to all. If the activity of the irradiation source is high and the irradiating measuring conditions are optimally designed, the use of Compton back scattered radiation becomes possible in radiography. For Cs137, the energy of the incident of Eθ when θ = 180o and θ = 90o of 184kev and 288kev respectively (Knoll1989). Americium 241: Pure Americium is a relatively soft radioactive metal with silvery appearances. Its most common isotopes are Am241 and Am243. Am241 source emits α- particles with known energies. It has a significantly longer half life than Pu238 (432.2 years vs 87 years). It has been proposed as an active element for both gamma rays and α- particles for a number of medical and industrial uses. The 60kev gamma ray emissions from Am241, the energy of the incident photon is equal to 60kev. This yields theoretical values of Eθ when θ = 180o and θ = 90o of 0.485Mev and 0.534Mev respectively (Knoll1989). Cerium 141: Cerium is a soft silvery ductile metal which easily oxidizes in air. There are four isotopes of Cerium that occur naturally. These are Ce141, Ce142, Ce138 and Ce136. Of all these four, Ce141 has a half life of 32.501 days. This element also has two metastable states. Cerium is a malleable, soft ductile iron grey metal, slightly harder than lead. It is very reactive. It tarnishes readily in the air. It oxidizes in the air; it oxidizes slowly in cold water and rapidly in hot water. It dissolves in acids. The incident radiation of Ce141 possesses energy of about 145.4 kev (Knoll1989). Monte Carlo simulation is developed to describe the interaction processes occurred when the photon beam coming in the medium containing the testing objects, the results of which are that only the photons that are back scattered within a solid angle covered by the detector collimator to be registered by the corresponding detector in the array. The registered back scattered events allowed then to reproduce the two dimensional image of the object, to determine the saturation thickness of the material for a given energy of gamma rays and to plot energy spectrum of the back scattered photons. In general simulation program can be used for the target material with multi-elemental constituents. |
III. SIMULATION |
| A Monte-Carlo simulation has been developed to describe the interaction processes of gamma rays when coming in a medium with infinite thickness. The photons emitted from a radiation source or X-ray tube is followed until they are lost by the photoelectric absorption in the medium or registered by the back scattering detector array. The collision of a gamma ray with free electrons is explained by the Compton interaction. The kinematic equations that describe the interaction are exactly the same equations as for two billiard balls colliding with each other, except that the balls are of different sizes. Fig. 1 shows the interaction. To illustrate the difference between the intensity computed with the vector and scalar equations. Fig. 2a shows the comparison between the vector and the scalar approaches for the whole backscattered spectrum for a sample of water (Fernandez, 1991). |
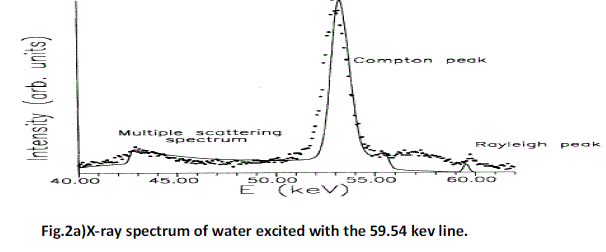 |
| 1. The incidence and take off angles are 45/135 respectively and azimuthal angle is φ=0º. 2. The solid line represents the theoritical estimation made by scalar transport equation (SHAPE) and the dotted line is done corrected with fourth-order collisions using Monte Carlo simulations (curve obtained from[J.E.Fernandez et.al.,1991: Sartori et.al 1992]). |
| In the above mentioned article, the intensities contributed by the Compton Effect depend on the coupled relationship between the scattered angle cosine and the wavelength shift which introduces some difficulties in the computation. There are four contributions involving the double scattering with the Rayleigh and Compton Effect: Rayleigh- Rayleigh, Rayleigh-Compton, Compton-Rayleigh and Compton- Compton. |
IV. RESULTS AND DISCUSSION |
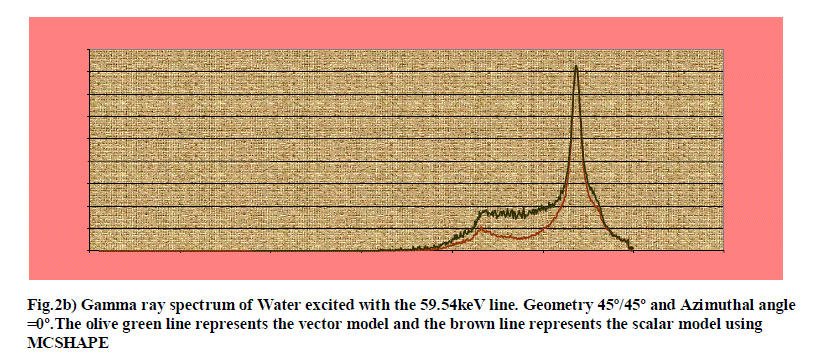
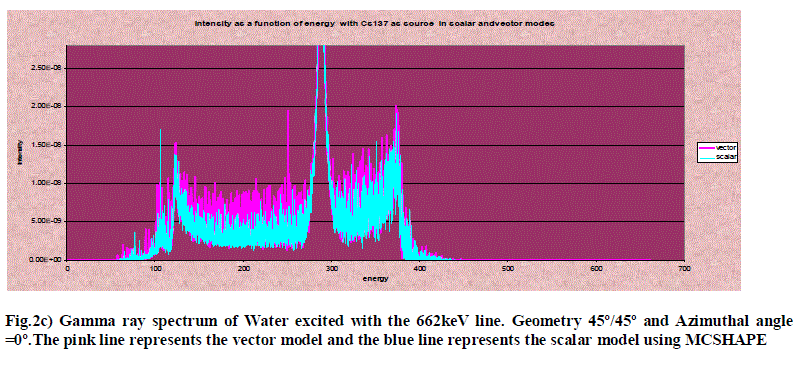
| The coupling between wavelength and direction prevents the separation of the phase-space integrals and make it necessary to separate them with mathematical tricks. Similarly in the case of Cs-137 and Ce-141 the Compton intensity due to these sources using MCSHAPE is observed. The scalar model gives only an approximated description of the photon transport because the scattering kernels are averaged on polarization states, and the photons propagate without changing the average state. A more advanced model was developed successively. From the fig. 2(b, c, d) it is clear that the sources with high energy i.e. 662kev has high intensity at the double scattering peak and also greater distortion. The influence of polarization is better appreciated if one is shown calculations of the same γ-ray spectrum with the scalar and vector theories. The coincidence of the vector model curve with the scalar model infers that as the number of collisions undergone is four therefore the intensity of the beam degrades the degree of polarization. |
 |
 |
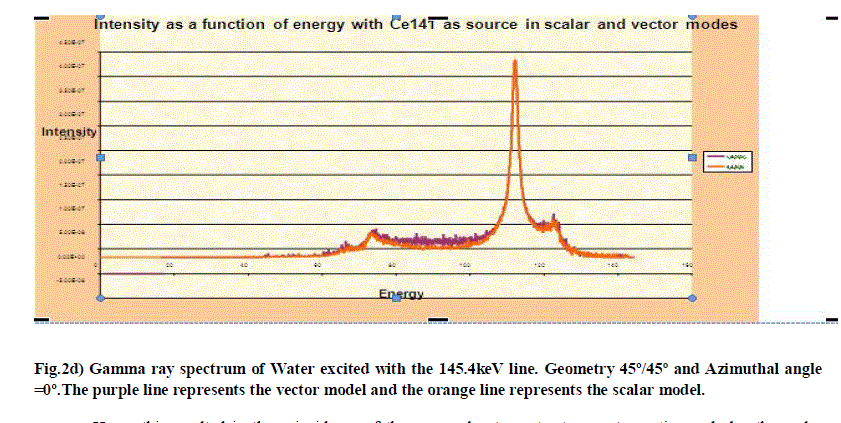 |
| Hence this resulted in the coincidence of the curves due to vector transport equation and also the scalar transport equation. In the fig. 2(b, c, d) it is further noted that at the double scattering peaks the in the case of Cs 137 the vector curve is indistinguishable from the scalar curve, this is because the backscattering is more in the detector due to this source whereas in the case of Ce141 also the backscattering in the double Compton peak is quite less when compared to Cs137. In the case of Am241 the vector model is easily distinguishable from the scalar model curve. This is because the backscattering is very low when compared to Cs137 and Ce141. If backscattering is high then that helps in the increased transmission through a flaw which results in a darker image on the developed film. Therefore the activity of the source is a critical characteristic since the quality of measurement is affected by backscattering. Too high backscattering adds fog to the film, darkening it overall and reducing the likelihood of identifying the flaw. Hence a radioactive source should be chosen in such a manner that the backscattering is low. Moreover the vector model is much better than the scalar model as the polarisation of the photons play a vital role in observing the image in the vector model than the scalar model which does not include polarisation. |
V. CONCLUSION |
| From these results, we conclude that the vector equation is a useful tool to compute the other stokes parameters, providing information about the state of polarization of the beam after each set of collisions. This is not possible with the scalar equation. Moreover the double scattering effect if reduced helps in observing the image more clearly in the gamma ray camera. After all MCSHAPE is the code of a simulated detector. Hence it can further be concluded that the source in the detector should be chosen in such a manner that it has low backscattering. |
References |
|