International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

New Results on Vertex Prime Graphs

Dr. A. Selvam Avadayappan1, R. Sinthu2
  1. Associate Professor, Department of Mathematics, V.H.N.S.N. College, Virudhunagar, Tamil Nadu, India
  2. Research Scholar, Department of Mathematics, V.H.N.S.N. College, Virudhunagar, Tamil Nadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

A graph G(V, E) is said to have a vertex prime labeling if its edges can be labeled with distinct integers from1, 2, 3, . . . , E such that for each vertex of degree at least 2, the greatest common divisor of the labels on its incident edges is 1. A graph that admits a vertex prime labeling is called a vertex prime graph. In this paper, we prove that mK3,3 and mK4,4 are vertex prime graphs, where m is any positive integer.

Keywords
labeling of graphs, vertex prime labeling of graphs.
Subject Classification Code (2000):05C(Primary)

INTRODUCTION
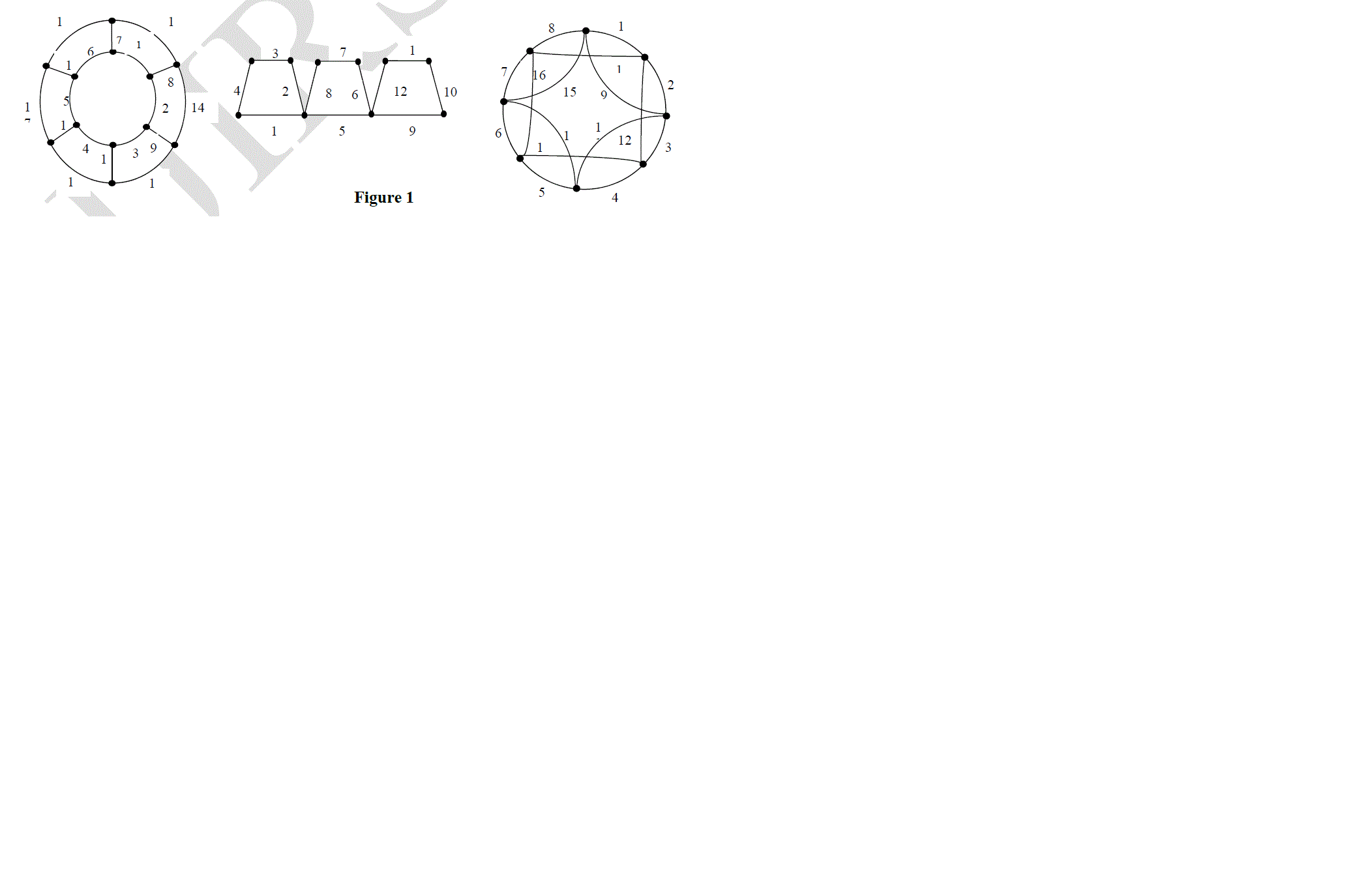image
image
image
image

BACKGROND OR RELATED WORK
Mean graphs and Super mean graphs are the related works.

PRESENTATION OF THE MAIN CONTRIBTION OF THE PAPER / SCOPE OF RESEARCH
We prove that mK3,3 and mK4,4 are vertex prime graphs through the definition of vertex prime graphs.We also work on the general case of this theorem.

EXPERIMENTAL RESULTS
We proved that mK3,3 and mK4,4 are vertex prime graphs.
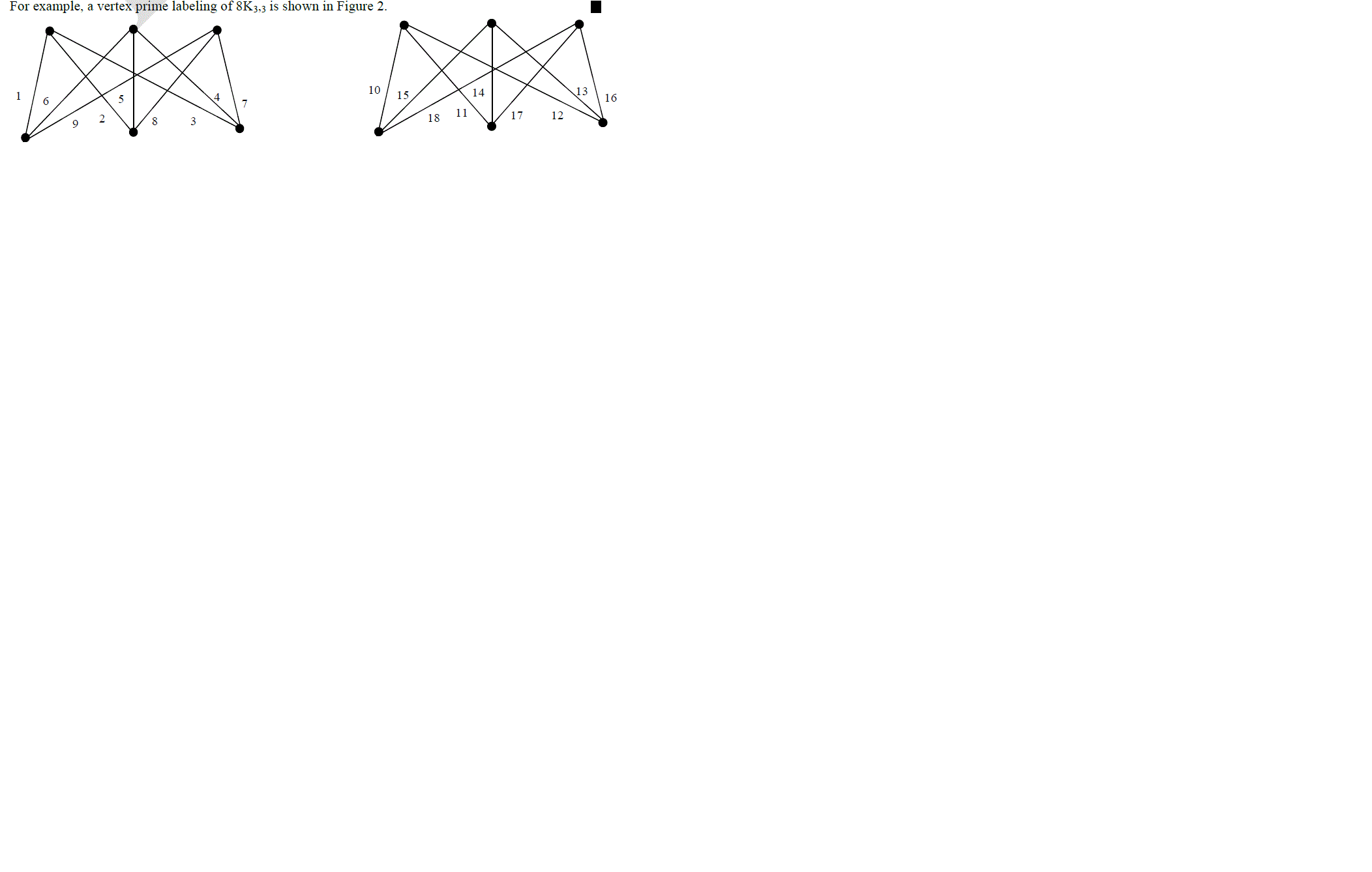
Theorem 1 For any positive integer m, the graph mK3,3 is a vertex prime graph.
Proof
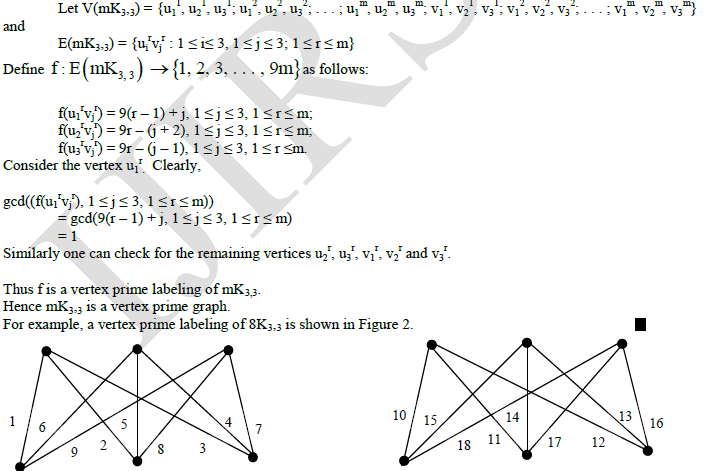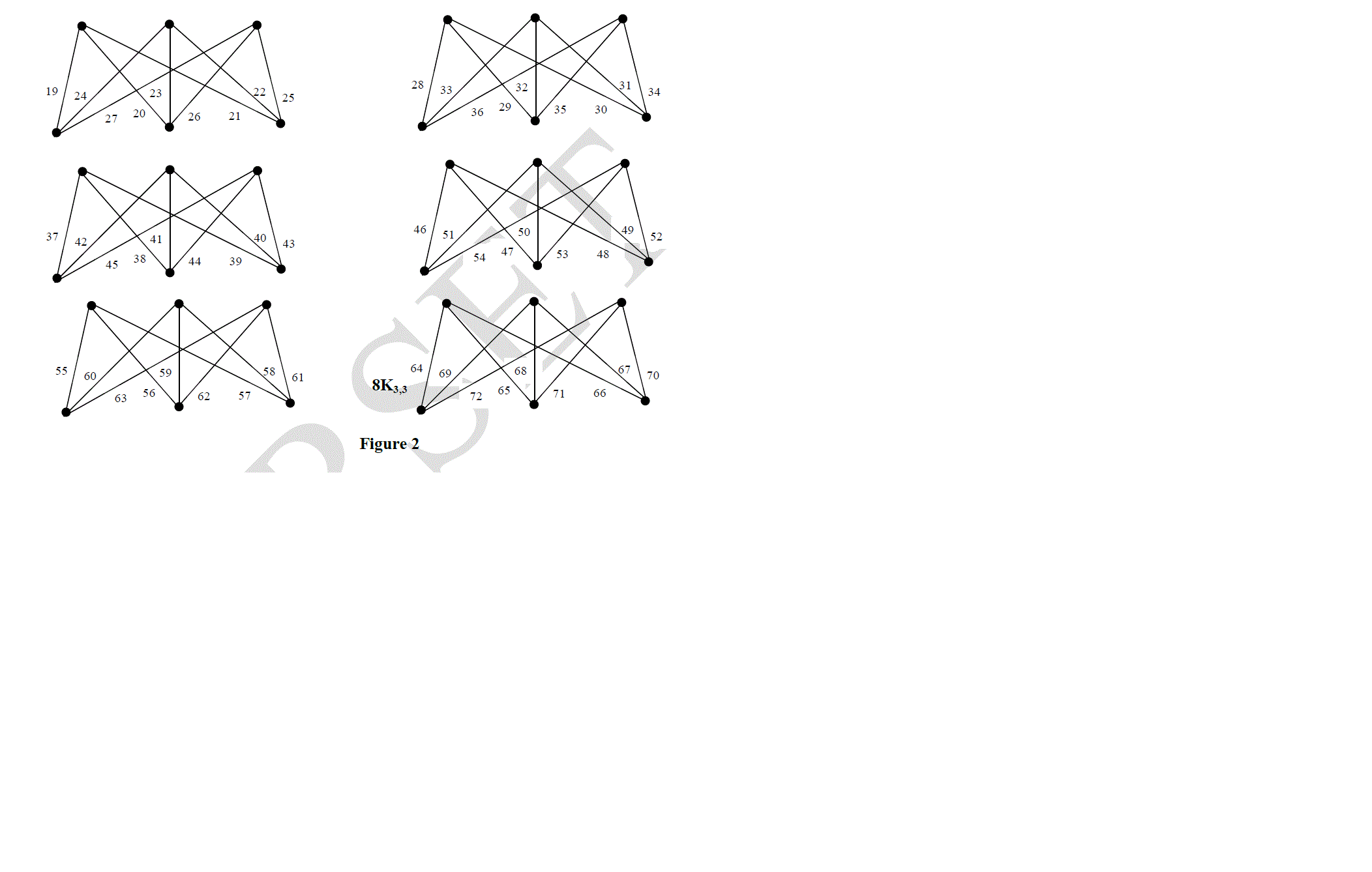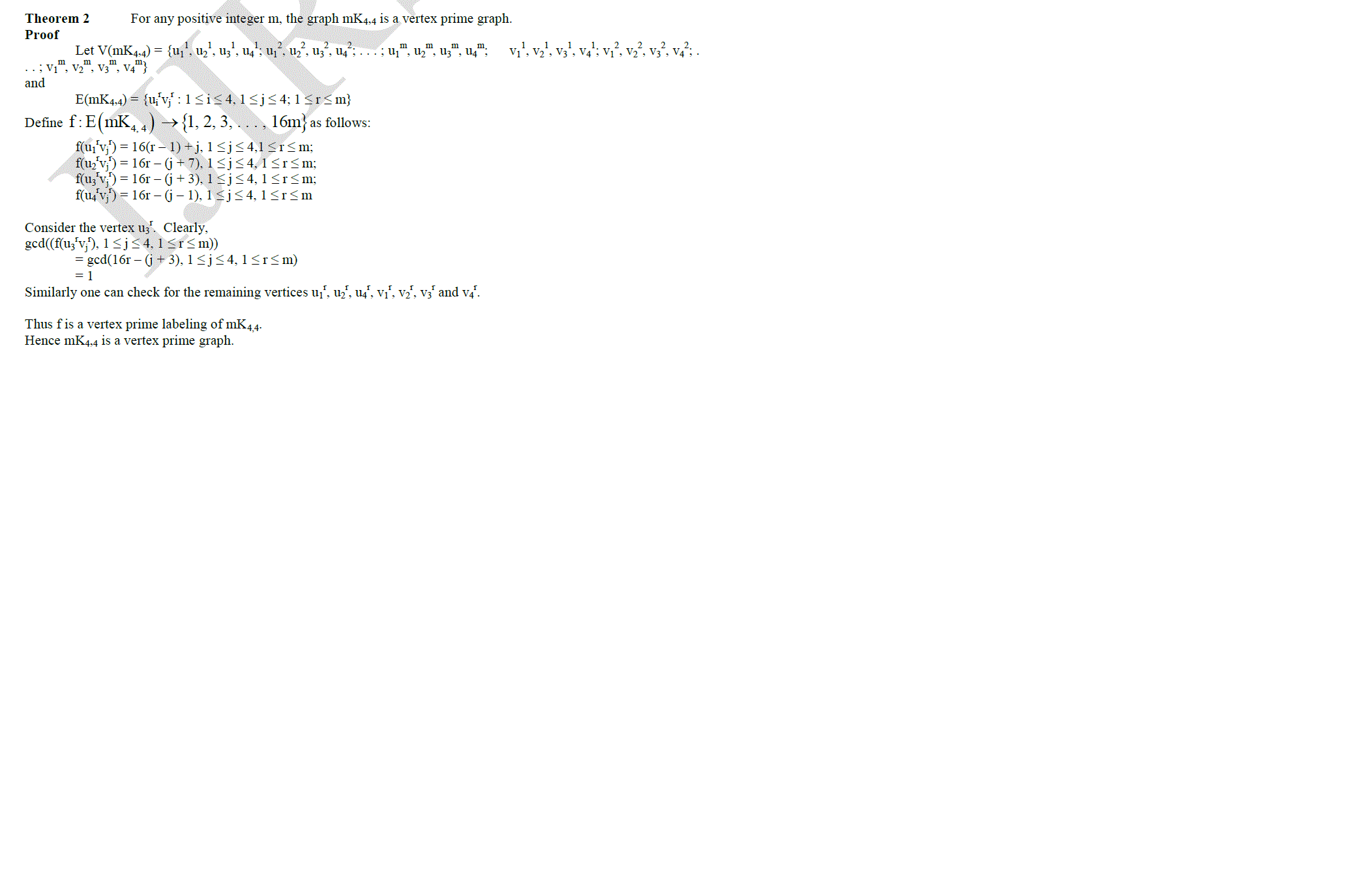
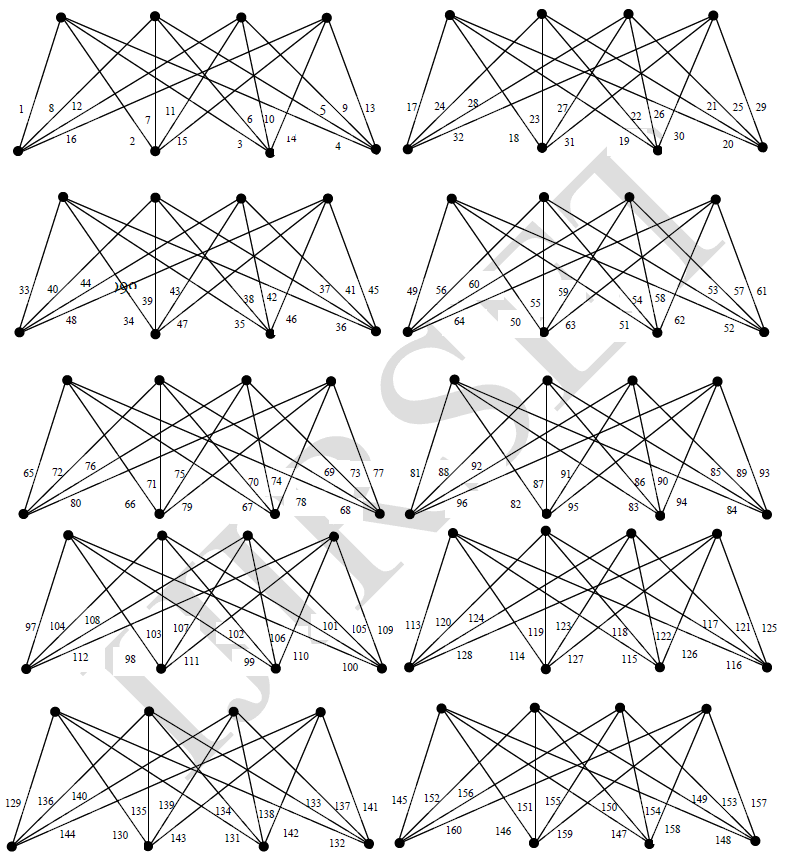
image
image
Theorem 2 For any positive integer m, the graph mK4,4 is a vertex prime graph.
Proof
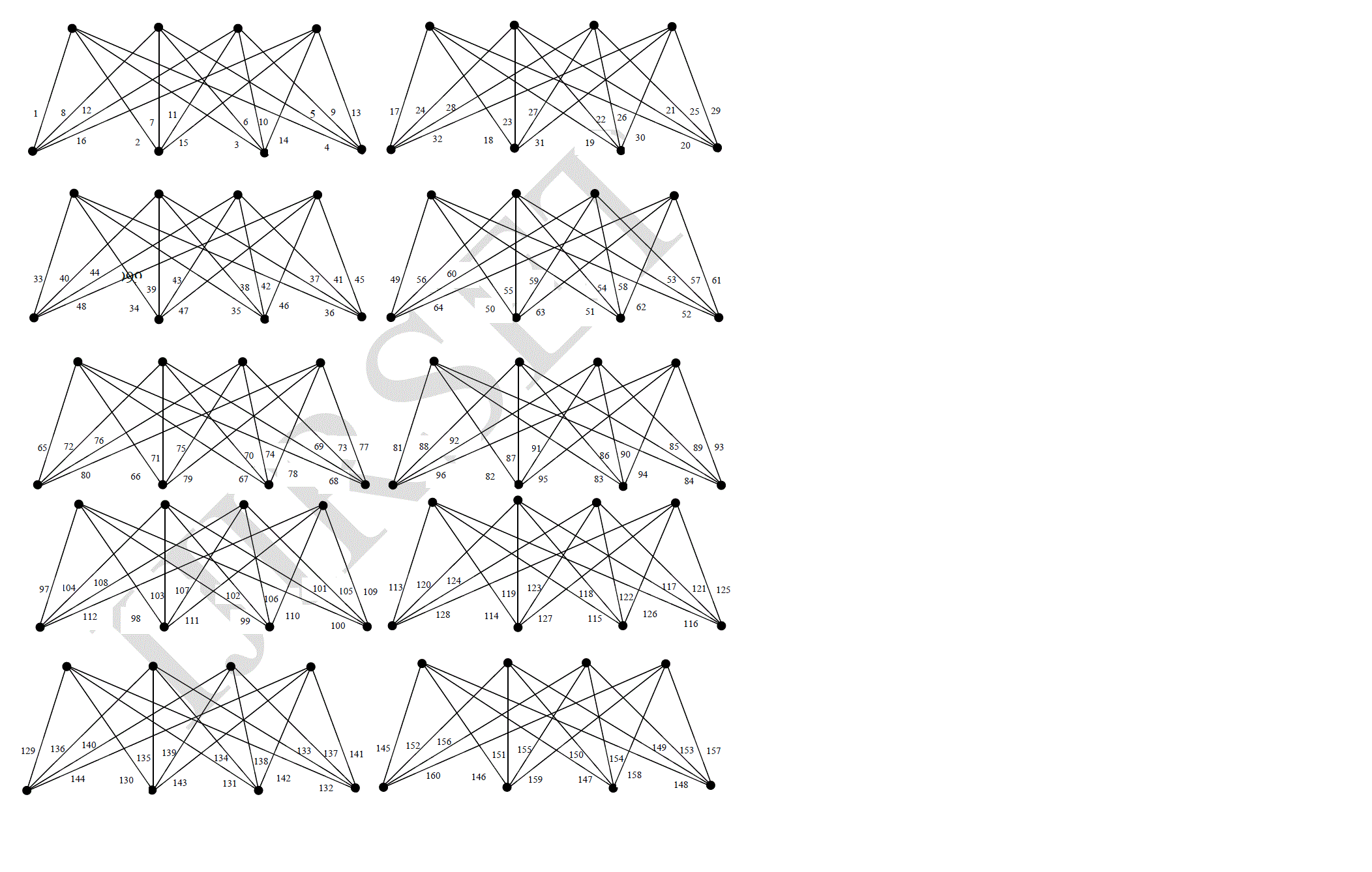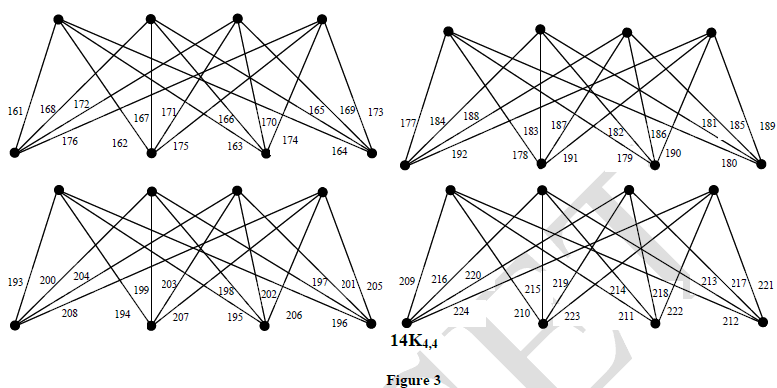image
image
image

CONCLUSION
In this paper, we present Vertex prime labeling if its edges can be labeled with distinct integers. Thus we prove that mK3,3 and mK4,4 are vertex prime graphs. Some known graphs and unknown graphs are illustrated in a simple manner.

ACKNOWLEDGEMENT
The authors of this paper would like to thank the reviewers for their valuable suggestions.

References
  1. Selvam Avadayappan and R. Sinthu,” mK2,3 is vertex prime”, International Journal of Physical Sciences, Vol. 20(3) M, pp. 613 – 618, 2008.
  2. R. Balakrishnan, and K. Ranganathan, A Text Book of Graph Theory, Springer Verlag (2000).
  3. I. Borosh, D. Hensley, and A. Hobbs, “Vertex prime graphs and the Jacobsthal function”, Congress Numerentium, Vol.127,pp.193 – 222, 1997.
  4. T. Deretsky, S.M. Lee, and J. Mitchem, “On vertex prime labelings of graphs”, in Graph Theory, Combinatorics and Applications Vol.1, J. Alavi, G. Chartrand, O. Oellerman and A. Schwenk, eds., Proceedings of 6th International Conference on Theory and Applications of Graphs (Wiley, New York, 1991), pp.359 – 369.