International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimal Reservoir Operation Using Genetic Algorithm: A Case Study of Ukai Reservoir Project

Sumitra Sonaliya1 and Dr. T.M.V. Suryanarayana2
  1. PG Student, Water Resources Engineering and Management Institute, Faculty of Technology and Engineering, The Maharaja Sayajirao University of Baroda, Samiala-391410, Vadodara, Gujarat, India
  2. Associate Professor, Water Resources Engineering and Management Institute, Faculty of Technology and Engineering, The Maharaja Sayajirao University of Baroda, Samiala-391410, Vadodara, Gujarat India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Application of optimization techniques for determining the optimal operating policy of reservoirs is a major issue in water resources planning and management. Genetic Algorithm is an optimization technique, based on the principle of natural selection, derived from the theory of evolution, are popular for solving optimization problems. The main aim of the present study is to develop a policy for optimizing the release of water for the purpose of irrigation. The fitness function used is minimizing the squared deviation of monthly irrigation demand along with the squared deviation in mass balance equation. The months considered are from July to October for three years from year 2007 to 2009. The decision variables are monthly releases for irrigation from the reservoir and initial storages in reservoir at beginning of the month. The constraints considered for this optimization are the bounds for the releases and reservoir capacity. Results show that in the year 2007, for months of July and August, 625 and 1573.86 MCM of water is saved respectively. In the year 2008, for July 65.67 MCM, August 27.15 MCM, September 35.32 MCM and October 62.91 MCM of water is saved. In the year 2009, for July 49.18 MCM, August 35.48 MCM, and in October 43.51 MCM of water is saved. Hence, GA model, if applied to the Ukai reservoir project in Gujarat State, India, can completely satisfy downstream irrigation demands and releases are minimized which leads to considerable amount of saving in water.

Keywords
Genetic algorithm, Optimization, Ukai reservoir project.

INTRODUCTION
Genetic Algorithms (GAs) are search procedures based on the natural genetics and natural selection. They combine the concept of the survival of fittest with genetic operators extracted from nature to form a robust search mechanism. Goldberg [1] identified the following differences between GAs and the traditional optimization methods:
• GAs work with coding of the parameter set but not with the parameters themselves.
• GAs search from a population of points, not a single point.
• GAs use objective function information, not derivatives or other auxiliary knowledge.
• GAs use probabilistic transitions rules, not deterministic rules.
Use of Genetic Algorithm (GA) in determining the optimal reservoir operation policies, is receiving significant attention from water resources engineers. A large number of works has been reported on the application of GA for various complex reservoir problems .East and Hall [2] has applied GA to a reservoir problem with the objective of maximizing the power generation and irrigation. Wardlaw and Sharif [3] evaluated several formulations of a genetic algorithm for four-reservoir, deterministic, finite-horizon problem. They also considered a nonlinear four-reservoir problem, one with extended time horizons and a complex ten-reservoir problem. They concluded that genetic algorithm approach is more robust. Sharif and Wardlaw [4] presented genetic algorithm approach for optimization of multireservoir systems for a case study in Indonesia and its results were compared with those of discrete differential dynamic programming. They concluded that genetic algorithm results are closer to the optimum. Kuo et al. [5] used genetic algorithm based model for irrigation project planning for a case study of Delta, Utah, for maximization of economic benefits for a command area. They compared solution of genetic algorithms with that of Simulated Annealing and iterative improvement techniques. Ahmed and Sarma [6] developed a GA model for deriving the optimal operating policy and compared its performance with that of stochastic dynamic programming (SDP) for a multipurpose reservoir. The objective function of both GA and SDP was to minimize the squared deviation of irrigation release. Sensitivity analysis was carried out for mutation and cross over. They found that GA model releases nearer to the required demand and concluded that GA is advantageous over SDP in deriving the optimal operating polices. Janga Reddy and Nagesh Kumar [7] developed Multi-objective Evolutionary Algorithm to derive a set of optimal operation policies for a multipurpose reservoir system and concluded that the results obtained using the proposed evolutionary algorithm was able to offer many better alternative policies for the reservoir operation, giving flexibility to choose the best out of them. Jotiprakash and Ganesan Shanthi [8] developed a GA model for deriving the optimal operating policy for a multi-purpose reservoir. The objective function was to minimize the squared deviation of monthly irrigation demand deficit along with the deviation in the target storage. Sensitivity analysis was carried out for crosses over and size of population, and they found that GA model releases nearer to the required demand and concluded that GA model is advantageous in deriving optimal operating polices. Mathur and Nikam [9] optimized the operation of an existing multipurpose reservoir in India using GA, and derived reservoir operating rules for optimal reservoir operations. Tripathy and Pradhan [10] developed a GA model for deriving optimal operating policy for Hirakud reservoir in India. The results obtained by GA model are compared with the current policy used by the Government of Odisha at that time and observed that GA gives a better policy. Srinivasa and Kumar [11] used the GA method to design the irrigation systems for a suitable cultivation pattern in India.
In the present study, a GA model has been used for optimum reservoir operation. The objective of this study is to minimize the squared deviation of monthly irrigation demand deficit along with squared deviation of mass balance equation. The decision variables used are the release for irrigation demand from the reservoir and initial storage in each month. The constraints used for this optimization are bounds for the releases and reservoir capacity.

STUDY AREA
The area selected for the present study is the catchment area of the Ukai dam, which is located across Tapi River near Ukai village of Fort Songadh taluka in Surat district. Its catchment is located between longitudes 73º32'25" to 78º36'3" E and latitudes 20º5'0" to 22º52'30" N. The dam is located at about 29 km upstream of the Kakrapar weir. The total catchment area of the Ukai reservoir is 62,225 sq. km, which lies in the Deccan plateau. The catchment of the dam covers large areas of 12 districts of Maharashtra, Madhya Pradesh and Gujarat. The districts that lie in the catchment include Betul, Hoshangabad, Khandwa, and Khargaon of Madhya Pradesh; Akola, Amravati Buldhana, Dhule, Jalgaon and Nasik of Maharashtra and Bharuch and Surat of Gujarat state. The command area of 66,168 Ha is spread over the districts of Surat, Tapi, Navsari and Valsad.

MODEL DEVELOPMENT
In the present study, the fitness function of the GA model is minimizing the squared deviation of monthly irrigation demand and squared deviation in mass balance equation. The objective function is given by equation 1.
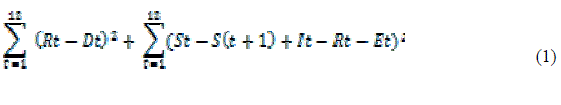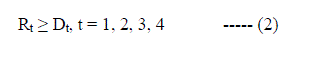Image
Image

RESULTS AND DISCUSSION
To apply Genetic algorithm (GA) to the above formulated model, the data used are inflow, demand, actual release, evaporation and storage in MCM. The important input variables in present GA model study are the monthly inflow in to the reservoir system and monthly irrigation demands for the month of July, August, September and October from year 2007 to 2009.The main objective of the study is to compute the quantity of water that should be released to meet the monthly irrigation demand. Since, the fitness function is based on the monthly irrigation demands (Dt) and monthly inflow in the reservoir (It), so reservoir releases for irrigation (Rt), and initial storage (St) in the reservoir in monthly time step are chosen as decision variable. Thus eight decision variables are considered for a year. The parameters considered in GA Population size from 5 to 20, probability of crossover of 0.80, number of generations from 5 to 50 and selection function Roulette wheel selection. After applying GA to the above formulated model the following results are generated which gives the releases by GA and that we consider as optimum releases for year 2007 to 2009.
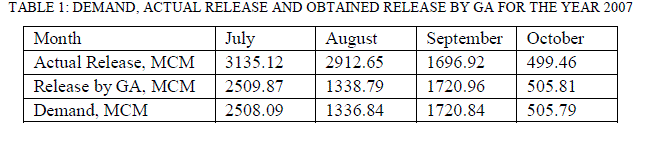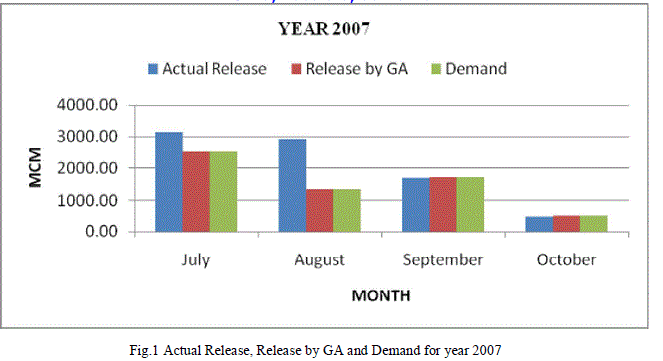
Image
Table 1 shows the values of the actual release, release obtained by applying genetic algorithm and the demand for each of the month of July, August, September and October for the year 2007. From the values of the Releases by GA, it can be shown that for each of the month of July, August, September and October, the demands are completely satisfied. Table 1 is represented graphically in Fig. 1.
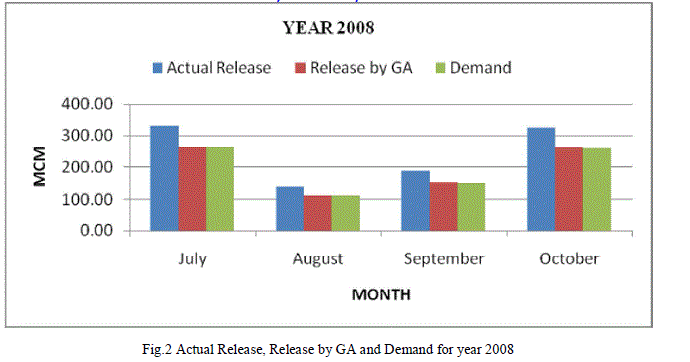
Image
Table 3 shows the values of the actual release, release obtained by applying genetic algorithm and the demand for each of the month of July, August, September and October for the year 2008. From the values of the Releases by GA, it can be shown that for each of the month of July, August, September and October, the demands are completely satisfied. Table 3 is represented graphically in Fig. 2.
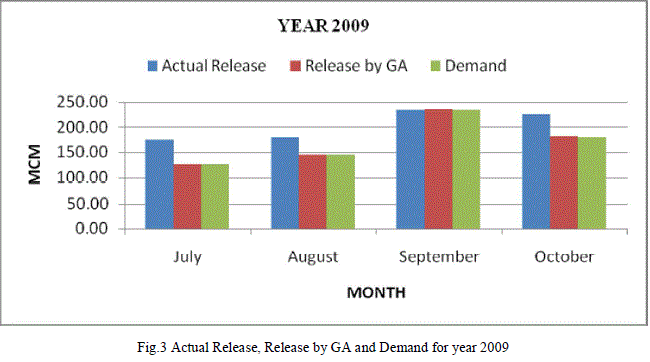
Image
Table 5 shows the values of the actual release, release obtained by applying genetic algorithm and the demand for each of the month of July, August, September and October for the year 2007. From the values of the Releases by GA, it can be shown that for each of the month of July, August, September and October, the demands are completely satisfied. Table 5 is represented graphically in Fig. 3.
Image
Table 6 shows the amount of water saved in MCM and in percentage for each of the monthS of July, August, September and October respectively for the year 2007. In the month of July, August and October, 49.18, 35.48 and 43.51 MCM of water is saved respectively in each month, which shows that almost 28 % of water is saved from the actual release in July and similarly almost around 20 % in August and October respectively. The asterisk (*) is used to show that the release obtained by GA is more than the actual release in the month of September, so water is not saved, but instead care is taken to fulfil the demands.

CONCLUSIONS
An optimal policy has been developed for release of water from the Ukai reservoir project for the purpose of irrigation. The releases developed by Genetic algorithm satisfy completely the irrigation demands for all the four months i.e. July, August, September and October for each year from year 2007 to 2009 respectively. The amount of water saved in the months of July and August for year 2007 is 625.25 MCM and 1573.86 MCM respectively, similarly in the months of July, August, September and October for year 2008, it comes out to 65.67 MCM, 27.15 MCM, 35.32 MCM and 62.91 MCM respectively and in July, August and October for year 2009, it is 49.18 MCM, 35.48 MCM and 43.51 MCM respectively. Thus, almost in nine out of twelve months the optimal releases obtained by genetic algorithm, are less than the actual releases, which leads to considerable amount in saving of water.

References
  1. Goldberg, D. E., “ Genetic Algorithms. In: Search, Optimization and Machine Learning”, Addison-Wesley, New York,1989.
  2. V. East,MJ Hall, “Water resources system optimization using genetic algorithms”, Proc.1st int. conf. on Hydroniformatics, Balkema,Rotterdam, The Netherlands, pp 225-231, 1994.
  3. Wardlaw, R. and Sharif, M., ‘Evaluation of genetic algorithms for optimal reservoir system operation’, Journal of Water Resources Planning and Management ASCE 125, 25–33, 1999.
  4. Sharif, M. and Wardlaw, R., ‘Multireservoir systems optimization using genetic algorithms: case study’, J. Comp. Civil Engin. ASCE 14, 255– 263, 2000.
  5. Kuo, S. F., Merkley, G. P. and Liu, C. W., ‘Decision support for irrigation project planning using a genetic algorithm’, Agri. Water Manage. 45, 243–266, 2000.
  6. Ahmed Juran Ali., Arup Kumar Sarma , “Genetic algorithm for optimal operation policy of a multipurpose reservoir”, Water resources management, vol-19, pp 145-161, 2005.
  7. Janga Reddy M.and Nagesh Kumar D. , “Multiobjective differential evolution with application to reservoir system optimization”, Journal of Computing in Civil Engineering, pp-861-878, 2005.
  8. Jotiprakash, V and Ganeshsan shanthi , “Single reservoir operating policies using genetic algorithm”. J. of Water Resources Management, vol.20: 917–929, 2006.
  9. Y. Mathur ,S. Nikam , “ Optimal reservoir operation policies using genetic algorithm”, Int. J. Eng Technol(2), 184-187, 2009.
  10. U.K.Tripathy , S.N Pradhan , Application of Genetic Algorithm for optimal operating policy of the multipurpose Hirakud reservoir of IWWA 44(4),2012, 315-320, 2013.
  11. K. Srinivasa Raju and D. Nagesh Kumar, “Irrigation Planning using Genetic Algorithms”.J. of Water Resources Management, vol.18: 163- 176, 2004.
  12. Hashemi, M.S., Barani, G.A, Ebrahimi, H., “Optimization of reservoir operation by genetic algorithm considering inflow probabilities (Case Study: The Jiroft dam reservoir)”, J. of applied science. vol. 8(11), pp. 2173-2177, 2008.
  13. WRDO., ‘Bhadra Reservoir Project’, Project report, Water Resources Development Organization, Government of Karnataka, Bangalore, India, 1986.