ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Nakandhrakumar R S, Seralathan S, Azarudeen A, Narendran V Department of Mechanical Engineering, Hindustan University, padur, Chennai, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The Job shop scheduling (JSS) problem consists of „n‟ jobs and „m‟ operations on each of the jobs and it is hardest combinatorial optimization problems for which it is extremely difficult to find optimal solutions. Past two decades, much attention has been made to general heuristics such as Genetic algorithm, Ant Colony Optimization, Tabu Search and Simulated Annealing to solve this type of combinatorial optimization problems. In this paper we present how the adaptive search algorithms namely Tabu search is applied to solve Job shop scheduling (JSS) problem. The method uses dispatching rules to obtain an initial solution and searches for new solutions in a neighborhood based on the critical paths of the jobs. Several benchmark problems are tested using this algorithm for the best makespan and the obtained results are encouraging when compared with benchmark values.
Keywords |
| Job shop scheduling, Optimization, Tabu Search, disjunctive graph |
I. THE SALIENT FEATURES OF JOB SHOP SCHEDULING PROB LEM |
| Scheduling is an important phase in Production Planning. It concern the allocation of limited resources to tasks over time and focuses on how best to use the existing components, takes into account technical production constraints. The objective of this problem is to find optimal schedule by minimizing the makespan. In recent years, many heuristic techniques such as Genetic algorithm, Ant Colony Optimization, Tabu Search and Simulated Annealing were employed to solve this type of combinatorial optimization problems. In this paper, an attempt has been made to solve job shop scheduling problem by heuristic technique called Tabu search (TS) for minimizing the makespan, which satisfy the precedence and capacity constraint. In JSS problem, set of „n different jobs & set of „m different machines are processed in a specified operation time with distinct task routes. |
| The standard model of the n-job, m-machine job shop problem is denoted by: n / m / G/ C*max. The parameter G indicates that jobs are connected with technological production rules, describing their processing order of machines. This order is specified in the technological matrix. An example for Technological matrix (G) could be |
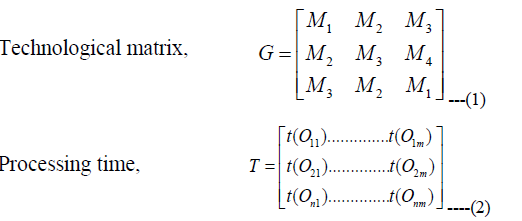 |
| The parameter C*max stands for the minimum makespan of the job shop and indicates the performance measure used to minimize the production time to finish all the jobs, taking into account the imposed restrictions of machine occupation. |
A. Representa tion Models |
| A schedule is defined by a complete and feasible ordering of operations to be processed on each machine and in job shop. There are two main ways of graphically representing such an ordering |
| • Gantt Chart |
| • Disjunctive Graph |
| 1) Gantt Chart: The simplest and most widely used representation method is the Gantt chart. This chart (Table 1) is a matrix illustrating the relationship of jobs and machines when idle time and starting and /or completion time are inserted. |
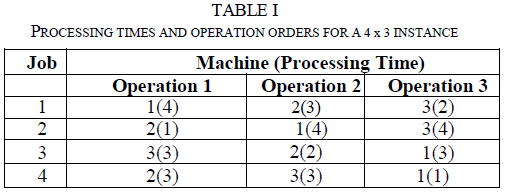 |
| 2) Disjunctive graph model: A job-shop scheduling problem is often represented by a disjunctive graph. In disjunctive graph vertices drawn as circles, represent tasks. conjunctive arcs, which are directed lines, represent precedence constraints among the tasks of the same job. Disjunctive arcs, which are pairs of opposite directed lines, represent possible precedence constraints among tasks belonging to different jobs, these tasks being performed on the same machine. A graph representation for the problem stated in Table 1 is shown in figure1 and a representation of disjunctive graph is given in figure 2. |
 |
II. LITERATU RE REVIEW |
| The Job Shop Scheduling problem has drawn interest during last decades, mainly because of its combinatorial characteristics. Previous decade researcher of Chambers et al., [3] presented, the Tabu search used to solve the problem of Job Shop Scheduling. This paper outlines the algorithmâÃâ¬ÃŸs implementation and performance when applied to job shop scheduling. In this paper some statistical analysis for parameter tuning is presented and the obtained solutions are compared with benchmark problems in job shop scheduling. |
| Ponnambalam et al. [4] considered the tabu search technique for solving job shop scheduling problems. The performance measure considered is makespan time. The adjacent pair wise interchange method is used to generate neighborhoods. The results of tabu search are compared with simulated annealing and genetic algorithms. It was concluded that the performance of tabu search is comparable to that of genetic algorithm and simulated annealing. |
| Farud Geyik et al., [5] focused on tabu search strategies and parameters such as initial solution, neighborhood structure, tabu list, aspiration criterion and number of iteration. This gives an introduction about tabu search and explores the meta-heuristic approach called tabu search, which is dramatically changing our ability to solve a host of problems in applied science, business and engineering. |
| Group shop scheduling problems have been solved by using Tabu search algorithm by Liu et al. [6]. They concluded that computational results by this algorithm are typically more efficient and faster than the other methods. |
| Jen-Shiang Chen et al., [7] have studied the re-entrant permutation flow-shop scheduling problem with objective to minimize makespan using Hybrid Tabu Search (HTS) method. They concluded that the improvement rate during computation can hardly be increased even a great amount of computational time is spent. Further, they suggested using dynamic tabu list instead of static tabu list for reducing effect of maximal iteration number and experimental design may be applied to find out the best way of neighborhood search. Same HTS used by Wojciech Bozejko et al., [8] for solving job shop problem with a no-wait constraint with a makespan criterion. Their main achievement of this work is a very high efficiency of an algorithm in a comparable time with other algorithms such as Genetic Algorithm, Neural network etc., |
| Multi-objective flexible Job Shop scheduling problems with three minimization objectives – the maximum completion time (makespan), the total workload of machines and the workload of the critical machine are considered simultaneously and solved using an effective hybrid tabu search algorithm by Jun-qing Li et al.,[9].They used an effective neighborhood structure with two adaptive rules for speed – up local search method in the neighborhood of tabu list. Finally they concluded that this method helped to improve the solution quality as well as the search speed in the operation scheduling module. |
| Mohammad Mahdi Nasiri et al., [10] used the hybrid algorithm which combines global equilibrium search(GES), path relinking and tabu search (TS) for solving Job shop scheduling problem. In which they used biased random sampling to have a better covering of the solution space. They concluded that proposed GESTS algorithm take advantage of a new version of N6 neighborhood and it is a very fast and effective algorithm. |
| Antonin Ponsich et al., [11] carried the JSS problem with the aim to determine if the association of Local Search procedure with a global search method was able to attain the same performance levels which includes very competitive re-start features. They concluded that the computational results indicated a very good general efficacy of the Differential Evolution – Tabu Search (DETS) algorithm for the mid-size problems with satisfactory repeatability and on complex instances observed that there is a deterioration of the solution quality. Further, they suggested that there is still room for improvement. |
III. TABU SEARCH |
| Tabu search [2] is a local search algorithm that requires a starting solution and a neighborhood structure. The procedure begins with an initial solution and stored it as the current seed and the best solution. The neighbors of the current seed are then produced by a neighborhood structure. These are candidate solutions. They are evaluated for an objective function and a candidates of which is not a tabu or satisfies the aspiration criterion is selected as a new seed solution. This selection is called move and added to tabu list in order to create memory. The new seed solution is compared with the current seed solution. If better, it is stored as new best solution. Iterations are repeated until a stop criterion is satisfied. |
A. Elements of TS Algorithms |
| The elements of the TS algorithm [2] in connection with job shop problem are defined as follows. |
| 1) Initial solution: A feasible solution is obtained by selecting from any one priority dispatching solutions. Initial solution affects the scheduling solution quality. In this paper, the shortest processing time (SPT) rule is used as an initial solutions method. |
| 2) Neighborhood Structure: A neighborhood structure is a mechanism, which contain new set of neighbour solutions by applying a simple modifications to given solutions. Each neighbour solution is reached from a given solution by move. A sequencing move is defined by the exchange of certain adjacent critical operation pairs and then considered the exchange of every adjacent critical operation pair on every machine. |
| 3) Move: The best neighbour which is not tabu or satisfies a given aspiration criterian is selected as a new seed solution. “The best” neighbours is one whose objective function Cmax is minimum. If the entire neighbour is tabu or no neighbour satisfies the aspiration criterion then the oldest neighbour entering the tabu list at first, is selected as new seed solution. |
| 4) Tabu list: The purpose of the tabu list is to prevent the search from degenerating by starting to cycle between the same solutions. In tabu list, the elements added on the list are attributive. The main aim of using an attributive representation is to save computer memory. The attribute that represents an element in sequencing is two operations that have interchanged in recent move. It is the arc (j,i), which is obtained by swapping a pair of operations (i, j). To identify tabu status of the neighbour (j, i) it is looked whether or not it is on the tabu list; if so it is labeled as “tabu”. Tabu list is updated after each move in so far as the strategic forgetting occurs. |
| 5) Aspiration criterion: The aim of the aspiration criterion, when it is necessary, is to override the tabu status of a neighbour. The aspiration criterion used as follows, if the move yields a solution better than the best obtained so far then the move is perfomed even as it is tabu. |
| 6) Termination criterion: When the number of disapproving moves reaches to a maximum to a maximum set value of 9000 or neighbour is generated or an infeasible solution is encountered. The TS algorithm terminates. |
 |
 |
IV. IMPLEMENTATION |
| Consider the technological matrix (1) and it should be defined into a disjunctive graph while using the tabu system for Job shop scheduling. For this, General Initial level is found for all the operations. The tabu list chooses the operation which is having higher probability value. The probability value depends upon the major tabu value and the heuristic distance for the particular job. The stored tabu is recorded and the time of operation to complete all the jobs. When the entire search completes a tour, a cycle is completed. Then the tabu which is having the minimum completion time is chosen and stored value is updated to this path of tour. After completing the total number of cycles, the final path of tour in tabu list is recorded. Then the makespan for the path is found to the machine order. Then using the makespan comparison graph of the output has been plotted in which shows deviations between the obtained makespan and benchmark values. |
V. RESULTS AN D DISCUSSIONS |
| The developed software for the proposed Tabu search algorithm has been tested for different bench mark problems proposed by Muth and Thompson (1963)(MT06), E. Taillard (1993) (TA00 – TA05), Fisher and Thompson (FT10), LA 05, ORB (10x10)(ORB 01 – ORB05). The obtained computational results are given in Table 2. |
| Figure 3 and 4 shows the comparison of makespan obtained by Tabu search and the optimum makespan known (Benchmark values) for various test instances are given in Table 2. |
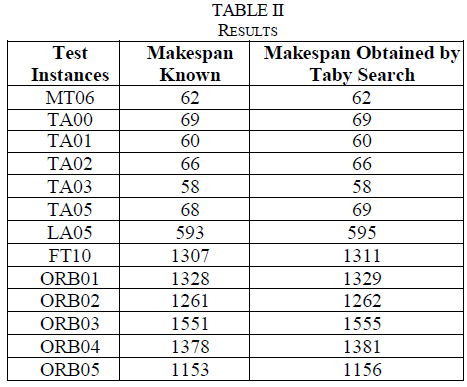 |
| From the table it is found that, obtained makespan value by Tabu search is very close to the benchmark value. But the deviation increase with the increase in complexity of the problems. |
 |
 |
| or less same and the deviations are found smaller while solving problems size up to 5 X 5. |
| Figure 4 shows that the deviations are found to increase a bit while solving problem size 10 X 10 and above. |
VI. CO NCLUSIONS |
| Job shop scheduling problems can be solved by many techniques like Genetic algorithm, Simulated annealing, Tabu Search, Ant Colony Optimisation Shifting Bottleneck Procedure, etc. In this paper, Tabu Search is applied to JSS problem to obtain best makespan. The approach seems to be a promising one because of its generality in nature and its effectiveness in finding very good solutions to the difficult problems. |
References |
|