ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Mythili.M1, Gowrishankar.V2, Venkatachalam.K.V3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Digital Signal Processing (DSP) systems are the core of wide range of applications like audio, video, image processing and consumer electronics.Most of the DSPs involve repetitive operations of addition, subtraction and multiplication on large integers.A digital Finite Impulse Response (FIR) filter performs the frequency shaping or linear prediction on a discrete-time input sequence {x0, x1, x2….}. In this work we focused on the design of an efficient VLSI (Very Large Scale integration) architecture for FIR filters which aims at reducing the power consumption, increasing the speed and also to reduce the hardware complexity using Residue Number System (RNS). This enables simultaneous parallel processing on all the digits resulting in high speed addition and multiplication in RNS domain. It uses modulo adders and modulo multipliers to obtain high speed performance.
Keywords |
| Finite Impulse Response (FIR), Residue Number System (RNS), modulo adders, modulo multipliers, moduli set. |
INTRODUCTION |
| The aim described in [1] was the comparison of RNS-FIR filter with TCS-FIR filter in terms of delay, area and power dissipation. And the work in [1] took into account the dynamic power dissipation, which was the dominant portion of the energy consumed a few years ago. The static powerdissipation is also an important role in today’s powerbudgets due to the technology scaling, and the increased transistor’sleakage due to sub-threshold current. In [2] the static and dynamic power dissipation of RNS filter was reduced compared to TCS filter, but the speed was not improved. |
| RNS implementation is faster than its TCS counterpart because the computations are accomplished in short word - length modulo channels without carry propagation between channels. As the carry chain that slows down Very Long Word- Length (VLWL) (hundred bits or more) addition and multiplication is effectively broken in RNS, the problem in implementing VLWL arithmetic on platforms with limited space and constrained battery specification, such as smart cards and Radio Frequency Identification (RFID) tags, is the hardware required for the conversion between TCS and RNS as well as the simultaneous computation in severalmodulo channels. As RNS is well suited for applications involving repetitive computations like repeated modulo multiplications in cryptographic algorithm and multiply-add operations in signal processing algorithm, the research emphasis has moved obviously in recent years to the area-power efficient implementation of concurrent modulo arithmetic operations in RNS. |
| The techniques such as multi-modulus and multi-function architectures to reduce the hardware redundancy as well as multi - threshold voltage and multi-supply voltage designs to lower the power dissipation have been proposed in [2]–[4]. Such control techniques are intended for algorithm level design space exploration and are applicable to generic modulo arithmetic architectures. For structural level simplification of specific modulo arithmetic operations like modulo multiplication, and modulo addition techniques that explore unique number theoretic properties of special moduli of the forms 2n, 2n+1, 2n-1 have received wide spread attention amongst others[5]-[8]. |
BACKGROUND |
| Residue Number System is widely used in the implementation of application specific Digital Signal Processing (DSP) systems. Since the system has gained a remarkable importance in recent years because of the lower power consumption over their two’s complement counterparts. |
| A. ResidueNumberSystem(RNS) |
| RNS is defined by a set of relatively prime integer. The RNS implementations can speedup addition, subtraction and multiplication. The data represented by RNS is processed in parallel with no dependence or carry propagation between the processing units. The process of converting the input data into RNS representation is called Forward Conversion, and the process of converting back the output data from RNS to conventional representation is called Reverse Conversion.A general structure of a typical RNS processor is shown in Fig 1. |
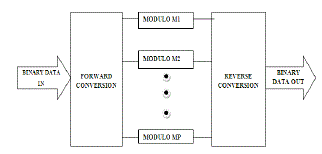 |
| In RNS, a decimal number is represented by an n-tuple of its remainders with respect to each modulus in the moduli set. To illustrate an RNS number, let us consider X to be a decimal number and set {m0, m1, m2…m(n-1)} to be the moduli set for a residue number system. This RNS can be the moduli set for a residue number system. This RNS can represent any number from 0 to (M-1), where M is the product of all the moduli in the set. Number X in this system will be represented as |
| <X >mi = X mod mi (1) |
| The operations of addition and multiplication in RNS, are done in parallel on the moduli |
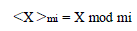 |
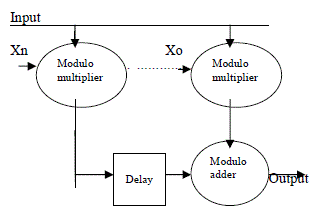
| This FIR filter can be implemented in RNS by decomposing it into p FIR filters working in parallel, as sketched in Figure 1. A key point in the design of the RNS filter is the selection of moduli. To select the set of co-prime numbers which cover the dynamic range of 20 bits, we used the tool described in [2], which selects the set of moduli giving the best delay/area/power tradeoffs according to the results of the characterization of the RNS filter composing blocks. In each tap, a modular multiplier is needed. |
| C.Modulo addition and modulo multiplication |
| Modulo addition and multiplication can be done by using special moduli set {2n, 2n+1, 2n-1}.These sets of forms are preferred over the generic moduli due to the ease of hardware implementation of modulo arithmetic functions as well as system level inter-modulo operations, such as RNS to binary conversions and signed detections. |
PROPOSED MODULO ADDER AND MODULO MULTIPLIER BASED RNS-FIR FILTER |
| Modular adder is one of the key components for residue number system (RNS) it can offer an excellent balance among the RNS channels for multi channel RNS processing. These adders are adopted to eliminate the recompilation of carries. It also offers better performance in delay and area. |
| A. Modulus 2n-1addition |
| As 2n-1is congruent to zero modulo, zero can be represented by an n-bit binary string of all zeros or all ones in modulo 2n-1arithmetic [10]. Thus, a modulo 2n-1addition oftwo operands, A and B is equivalent to an n-bit addition of A, B and Cout, i.e., |
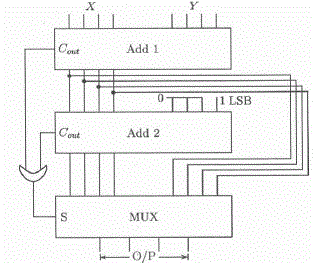 |
 |
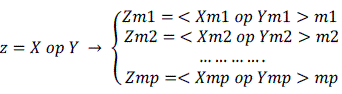 |
 |
| Modulo 2n+1operator are also commonly included in residue number system (RNS) applications. |
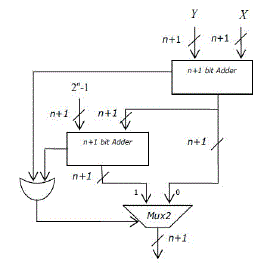
| C.Modulus2n-1multiplication |
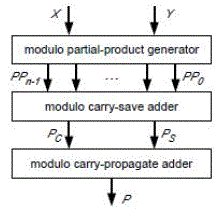
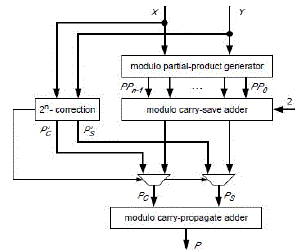
| For multiplication various ROM based solutions using table lookup have been proposed and compared. Sophisticated methods exist to reduce the table sizes by combining smaller table lookups with simple arithmetic operations, such as additions. For word lengths larger than eight bits, however, these solutions still require prohibitively large ROMs or many clock cycles for evaluation. For high performance modulo multiplication, keen multipliers are necessary, that can be implemented as combinational or pipelined circuits. Solutions based ordinary integer multiplication with subsequent modulo correction using adders are proposed. A modulo (2n-1) multiplier Architecture can be represented in Fig. 4. |
 |
| Modulo multiplication can be formulated as |
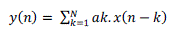 |
| D.Modulus2n+1multiplication |
| Modulo (2n+1) multiplication is considered here for the application of IDEA cipher. That is, n-bit numbers in normal representation are used for operands and result, where the value 0 is not used and the value 2n is represented by “00…._0”. The presented algorithm can easily be suited for number representations with the value 0 included and the value 2nindicated by a separate bit. |
| The normal number representation of modulo (2n+1) multiplication can be formulated as |
| X.Y mod (2n+1) |
| = (X.Y mod 2n -X.Y div 2n)mod(2n+1) (8) |
 |
| As well to modulo (2n-1) multiplication, an n-nbit unsigned multiplication followed by an n-nbitmodulo (2n+1) subtraction can be performed [3]. Again, the multiplication can be obtained by performing partial product generation and carry save addition modulo (2n+1). |
| E.Implementation of FIR filter by using modulo adders and modulo multipliers |
 |
| A main point in the design of the RNS filter is the choice of moduli. The special moduli set is considered here in the form of {2n, 2n+1, 2n-1}. |
 |
| Results for filter implementation |
| The uses of modulo adder and modulo multiplier in each tapgiving the best delay/area/power tradeoffs according to the results of the characterization of the RNS filter composing blocks. Adder and subtractor based forward and reverse converters are used in the design of FIR filter. The output of forward converter is given as the input to modulo adder/multiplier based RNS-FIR. The residue output from RNSFIR filter is applied to reverse converter, to achieve high speed of the filter output. |
RESULTS AND ANALYSIS |
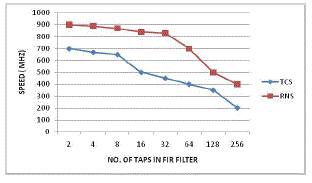
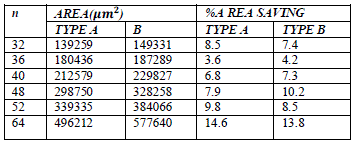
| In Table I the comparison is carried out on filters executed in the 90 nm STM library of standard cells (VDD = 1:0 V , at 25 C) [3], and the power dissipation has been calculated by Synopsys Power Analyzer based on the annotated switching activity of random generated inputs. All the filters can be clocked atfmax = 500 MHz.The power dissipation is computed at a clock frequency of 100 MHz. The speed of the FIR filter is improved than the traditional TCS-FIR. Table II represents the comparison of area saving between two modulo multipliers. The speed performance of residue number system based FIR filter is compared with the traditional Two’s complement system based FIR filter. Assuredly the performance improvement factor speed is improved much better than the conventional system. |
 |
CONCLUSION |
| One of the most widely used operations in DSP is Finite Impulse Response (FIR) filtering. Thus the design of compact and high speed real-time digital filters will be necessary to find applications in radar, communications and image processing systems.So the performance improvement in FIR filter using Residue Number System with modulo adders and modulo multipliers will be designed. The implementation of the proposed FIR filter has lesser delay than the conventional method. Due to the decrement of delay the speed of the system will be increased automatically.The implementation results show that the RNS filters offer a reduction offer a total power reduction of 35% with respect to the corresponding conventional filters. |
ACKNOWLEDGMENT |
| The authors acknowledge the contributions of the students, faculty of VelalarCollege of Engineering and Technology for helping in the design of check circuitry, and for tool support. The authors also thank theanonymousreviewers for their thoughtful commentsthat helped to improve this paper.The authors would like to thank the anonymous reviewers for their constructive critique from which this paper greatly benefited. |
References |
|