International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Physical and Optical Properties of Ge10Se90-xSbx Glasses

Atul K Kukreti1*, Shilpa Gupta1, Manish Saxena1 and Nikhil Rastogi2
  1. Assistant Professor, Department of ASH, Moradabad Institute of Technology, Moradabad, UP, India
  2. Director, School of Sciences, IFTM University, Moradabad, UP, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Chalcogenides glasses doped with antimony (Sb) have shown remarkable potential in nonlinear and optoelectronic applications. In search of finding the optimised glass for the use in infra-red optics the new ternary Ge10Se90-xSbx (x = 0, 3, 6, 9, 12, 15, 18, 21, 24) system has been studied theoretically for variation in physical parameters. Transmission spectra for Ge10Se80Sb10 have been used to study the absorption and refractive index of the material. The compositional variation of Sb (Replacing Se) on the system has been studied in terms of average coordination number, cohesive energy, glass transition temperature and transmission spectra of the system.

Keywords
Chalcogenide glasses, Glass transition temperature, Transmission spectra, Refractive index, Optical band gap.

INTRODUCTION
The elements in Group VI of periodic table S, Se, and Te along with more electropositive element such as Antimony (Sb) forms a special class of chalcogenide glasses. The phase change properties of chalcogenides make them attractive candidates to be used in all-optical devices [1]. Chalcogen glasses are generally less weakly bonded materials than oxide glasses. The alloy of Se- Sb improves the corrosion resistance and optical sensitivity of the alloy [2]. The addition of Ge and Sb with Se makes the material more promising glasses, having low transmission loss and high transparency to infrared radiations from 2 - 16 μm [3]. Ge-Se and Sb-Se glasses are promising materials for infrared optical fibres not only due to their high non-linearity and refractive index but also to their relatively good thermomechanical and chemical properties. The versatile behaviour of these materials makes us select this composition and study the effect of Sb in corporation in physical properties of Ge- Sb -Se glass. Physical interpretation and their results show Ge10Se90-xSbx (x = 0, 3, 6, 9, 12, 15, 18, 21, 24) as the most cross linked and stable. The addition of metallic impurity to glass alloy increases the conductivity and is very suitable for device fabrication [4].

II. MATERIALS AND METHODS
Thin films Ge10Se80Sb10 were deposited using thermal evaporation technique. The transmission spectra of these thin films were obtained using a double beam UV–VIS–NIR spectrophotometer. The slit width was kept at 1 nm and all the measurements were performed at room temperature (300K). The transmittance and reflectance measurements were carried out on a double beam spectrophotometer over a range 400 nm to 900 nm. Almost all the recording spectrophotometer uses a double beam principle and all achieve automatic control by suitable use of servomotors. In dual beam spectrophotometer, one beam provides a reference signal and the other a measuring signal. The blank (reference) is placed in the first beam and the sample in second. By referring intermittently or continuously to the reference beam when making measurements, errors that arise from fluctuations and drift in applied voltage, source intensity detector response, amplifier gain and other irregularities, as well as, those errors that the blank is particularly designed to compensate, are largely eliminated. A monochromatic source splits into two identical beams using a rotating sector mirror which alternately passes and reflects the beam directed at it (in some spectrophotometers), while in some other cases a stationary splitting device is used, in such cases two detectors are required. Either the difference or the ratio of their outputs is determined, amplified and presented, while where splitting is achieved by chopper, detection can be performed by either dual detectors or a single detector. In recording spectrophotometer once a sample and a reference are in place and controls are set, it determines and records the absorption curve of sample over one or more spectral ranges. For recording R and T spectral curved over the range 400-900 nm glass slide was used as reference in the present investigations.

III. THEORETICAL STUDIES AND DISCUSSION

3.1 MAXWELL’S COUNTING FOR FLOPPY MODES &AVERAGE COORDINATION NUMBER
According to J. C. Phillips it may be valuable to consider the transitions between Z = 2.4 and 2.67 in the light of the constraint – counting argument originally proposed for amorphous covalent materials [5]. Phillips gave the mechanicalconstraint counting algorithms to explain glass forming tendencies. The strongest covalent forces between nearest neighbours serve as Lagrangian (mechanical) constraints defining the elements of local structure (building blocks). Constraints associated with the weaker forces of more distant neighbours must be intrinsically broken leading to the absence of long-range order. The well known Phillips–Thorpe approach is based on comparing the number of atomic degrees of freedom with the number of inter-atomic force field constraints. If the number of degrees of freedom is greater than the number of constraints, the network is “floppy”; conversely, if the network becomes over-constrained, stressed-rigid structures will percolate throughout the entire network. According to Phillips, the tendency of glass formation would be maximum when the number of degrees of freedom exactly equals the number of constraints. For the composition Ge10Se90-xSbx (x = 0, 3, 6, 9, 12, 15, 18, 21, 24). The average coordination number Z was calculated by using the standard method [6].
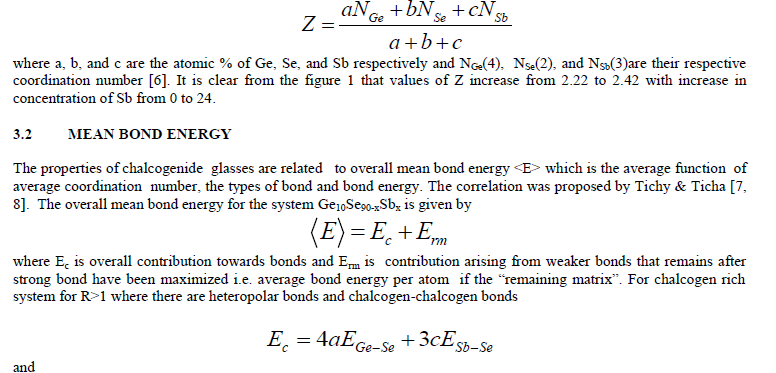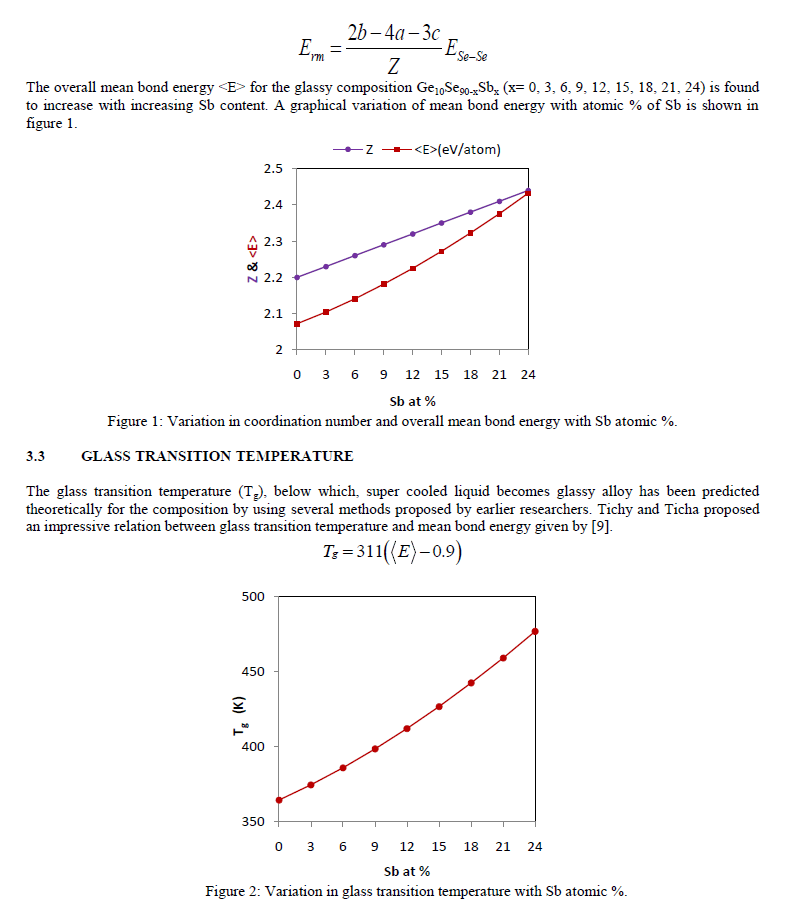image
image
The variation of Tg, corresponding to <E> and with increase in Sb content is shown in figure 2, which is clearly depicting the rise in glass transition temperature with increasing the content of Sb from 0 to 24 atomic % for the present composition. 3.4 COHESIVE ENERGY The cohesive energy of the system, defined as the stabilization energy of an infinitely large cluster of material per atom, has been calculated using the Chemical Bond Approach (CBA) [10]. According to CBA, atoms combine more favourably with atoms of different kind until all the available valences of the atom are filled. Bonds are always formed in the sequence of decreasing bond energies, which are assumed to be additive in nature. The heteropolar bond energies can be calculated by the relation [10].
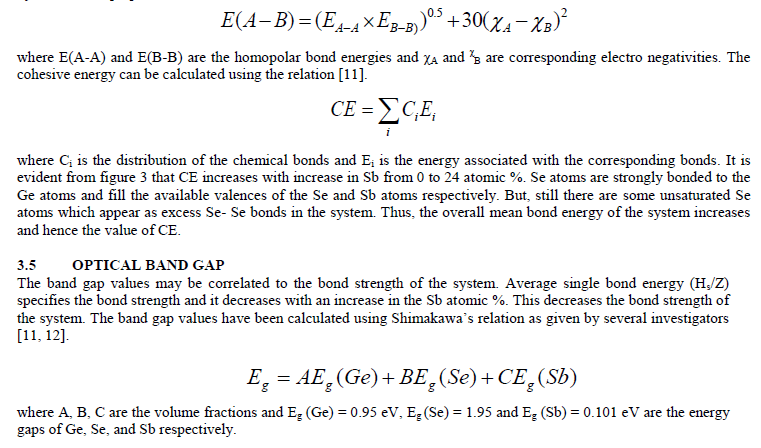image
Figure 3: Variation in cohesive energy and energy band gap with Sb atomic %. The variation of Eg with increase in content of Sb follows from the above discussion. figure 3 shows that values of Eg decrease from 1.940 to 1.468 with increase in concentration of Sb from 0 to 24 atomic %.

IV. OPTICAL STUDIES AND DISCUSSION

4.1 TRANSMISSION SPECTRA
Transmission spectra of Ge10Se80Sb10 thin films shows that the transmission shifts towards longer wavelength with Sb addition to the ternary system. A red shift has been observed in interference free region of spectra shown in figure 4. In the region of weak and medium absorption where (α ≠ 0), the transmittance decreases mainly due to the effect of absorption coefficient (α) and the refractive index (n). In the region of strong absorption, the transmittance decreases drastically, due to almost exclusively the influence of α and n whose values can be estimated by extra plotting the values in other region.
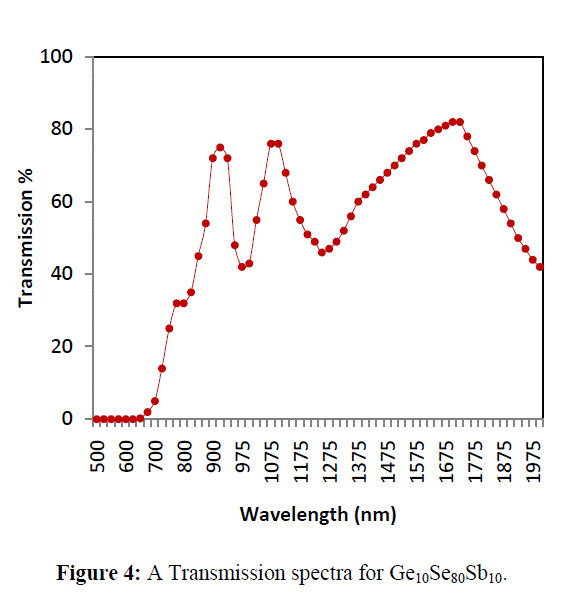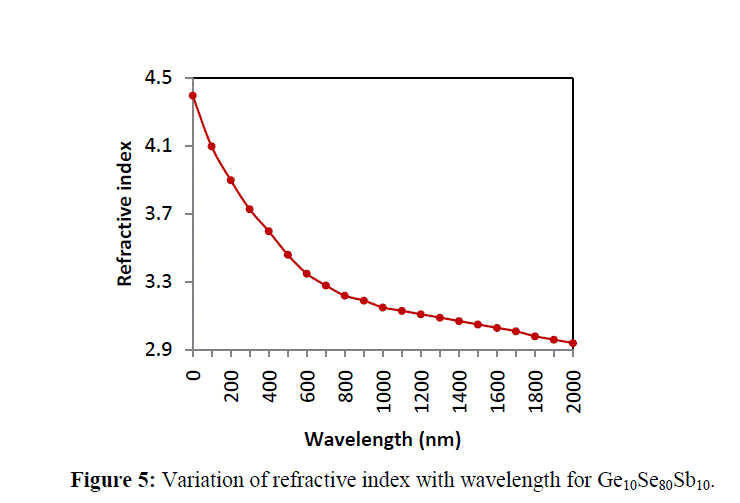
image

4.2 REFRACTIVE INDEX
The variation in refractive index has been explained using polarizability of atoms. The refractive index (n) and polarizability are linked by the relation given by Lorentz – Lorentz [13]
where n is the refractive index of alloy, αi is the polarizability and ε0 is the permittivity of the free space and Ni is the number of polarizable units per unit volume. As depicted from figure 5, the replacement of Se with Sb (different polarizable) leads to a variation in refractive index of the system [14]. The variation in the value of k with addition of Sb content indicates that loss of light changes due to scattering. A shift change evident from the Kramers–Kronig relation also supports the variation in refractive index [15, 16].
image

V. CONCLUSIONS
The average coordination number and overall mean bond energy increases and hence glass transition temperature increases because coordination no and heat of atomization of Sb are greater than that of Se. The cohesive energy increases slightly and energy band gap of the system decreases due to decrease contents of chalcogen Se and increasing Sb. The steadily shift change in transmission spectra and decrease in refractive index at higher wavelength makes these materials potential candidate for ultra high-band width signal processing and infrared optical sensors for medical applications.

References
  1. Abdel Rafea M. and Farag A.A.M., “Preparation and optical properties of SeS thin films semiconducting chalcogenide glasses”, Chalcogenide Letters, Vol. 5, No.3, pp. 27 - 33, 2008.
  2. Sharma P., Sharma V. and Katyal S.C., “Variation of optical constants in Ge10Se60Te30 thin film”, Chalcogenide Letters, Vol. 3, No. 10, pp. 73 - 79, 2006.
  3. Majeed Khan M.A., Kumar S., Hussain M. and Zulfekuar M., “Thermal properties of Selenium-Bismuth glassy alloys”, Chalcogenide Letters, Vol. 4, No. 12, pp. 147 - 153, 2007.
  4. Mehta N., Zulfequar M. and Kumar A., “Crystallization Kinetics of some Se–Te–Ag chalcogenide glasses”, J. Optoelectronics and Advanced Materials, Vol. 6, No. 2, pp. 441 - 448, 2004.
  5. Phillips J.C., “Topology of covalent non-crystalline solids I: Short range order in chalcogenide alloys”, J. Non- Crystalline Solids, Vol. 34, pp. 153-181, 1979.
  6. Thorpe M. F., “Continuous Deformation in Random Net-work”, J. Non- Crystalline Solids, Vol. 57, No. 3, pp. 355-370, 1983.
  7. Tichy L. and Ticha H., “On the Chemical Threshold in Chalcogenide Glasses”, Materials Letters, Vol. 21, No. 3-4, pp. 313-319, 1994.
  8. Tichy L. and Ticha H., “Covalent Bond Approach to the Glass Transition Temperature of Chalcogenide Glasses”, J. Non- Crystalline Solids, Vol. 189, No. 1-2, pp. 141-146, 1995.
  9. Biecerano J., Ovshinsky S. R., “Chemical bond approach to the structures of chalcogenide glasses with reversible switching properties”, J. Non- Crystalline Solids, Vol. 74, No. 1, pp. 75-84, 1985.
  10. Kukreti A. K., Gupta S., Saxena M., “Theoretical aspects in physical Properties of Se70Ge10Te20-XSbX Chalcogenide glass system”, International J Innovative Research in Science, Engineering and Technology, Vol. 2, No. 11, pp. 6074-6080, 2013.
  11. Tiwari R. S., Mehta N., Shukla R. K. and Kumar A., “Kinetic Parameters of Glass Transition in Glassy Se1−xSbx Alloys”, Turk J Phys , Vol. 29, pp. 233 – 241, 2005.
  12. Zakery A., Elliot S.R., “Optical Properties and Applications of Chalcogenide Glasses: A Review”, J. Non- Crystalline Solids, Vol. 330, No. 1-3, pp. 1, 2003.
  13. Gonzalez J.M., Prieto-Alcon R., Angel J.A. and Marquez E., “Optical Properties of Thermally Evaporated As40S60–xSex Films”, J. Non- Crystalline Solids, Vol. 315, pp. 134 – 143, 2003.
  14. Saxena M. and Bhatnager P.K., “Crystallization Study of Te–Bi–Se Glasses”, Bull. Mater. Sci., Vol. 26, No. 5, pp. 547–551, 2003.
  15. Borisova, Z.U., “Glassy Semiconductors”, Plenum Press, New York, 1981.
  16. Sharma P., Katyal S.C., “Far-infrared Transmission and Bonding Arrangement in Ge10Se90-xTex Semiconducting Glassy Alloys”, J. Non- Crystalline Solids, Vol. 354, No. 32, pp. 3836-3839, 2008.