Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Predicting Reservoir Water Level Using Artificial Neural Network

Shilpi Rani1, Dr. Falguni Parekh2
  1. PG Student, Water Resources Engineering and Management Institute, Faculty of Technology and Engineering, The Maharaja Sayajirao University of Baroda, Samiala-391410, Vadodara, Gujarat, India
  2. Offg. Director & Associate Professor, Water Resources Engineering and Management Institute, Faculty of Technology and Engineering, The Maharaja Sayajirao University of Baroda, Samiala-391410, Vadodara, Gujarat India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Water resources management mainly deals with hydrological forecasting. In hydrological forecast mainly forecast of water level of reservoirs is done which is useful for various purposes. Forecasting techniques may be different as per the purpose of system, data available for the system and physical characteristics. Uncertainty is there in hydrological parameters, and to deal with thisa proper forecasting method is needed. This paper presents an Artificial Neural Network (ANN) approach for forecasting of reservoir water level using ten daily data of inflow, water level and release. For developing the ANN models, three alternative networks i.e. Cascade, Elman and Feedforward back propagation were evaluated. A total of 23 years of hydrological data were used to train and validate the networks. This paper investigates the best model to forecast water level. The developed models are trained and validated on the collected data of Sukhi Reservoir project, located in Gujarat State, India.Based on these results, it can be concluded that amongst the three methods used for this study, ANN using Feed Forward Backpropagation is an appropriate predictor for real-time Water Level forecasting of Sukhi Reservoir Project.

Keywords
Artificial Neural Network, Forecasting, Release, Reservoir Inflow, Water Level

I. INTRODUCTION
Due to Advanced technology solutions, lot of data can be handled and data analysis become easier and faster. In water resources it becomes necessary to analyze the data and use the analyzed data for optimum use of water resources as there is scarcity of such resources. From last few decades, time series forecasting has achieved tremendous response from researchers.This stream has very wide applications. Previous, the traditional methods of time series analysis were used by the researchers. Traditional methods of time series analysis such as autoregressive method of Box - Jenkins (AR), auto-regressive moving average (ARMA), auto-regressive integrated moving average (ARIMA), autoregressive moving average with exogenous inputs (ARMAX), etc. The conventional time series modeling methods were also efficient since long time, but they suffer the problem of stationary and linearity and gives only reasonable accuracy. The need for giving more accurate forecast for time series has forced the researchers to develop innovative methods to model time series. Artificial Neural Networks (ANNs) were introduced as an efficient tools of modeling and forecasting since two decades. The artificial neural networks can model, map, and as well as can demonstrate the nonlinear relationship of complicated phenomena. The artificial neural networks are widespread and highly flexible function approximates, used in the fields of cognitive science and engineering. The artificial neural networks are widely used and have become increasingly popular in a broad range of fields. The neural networks are fewer sensitive to the error term assumptions and can bear noise, hectic components, and hefty tails better than most other methods. This paper presents a study aimed at forecasting water level of reservoir using neural network approaches.
The development of Artificial Neural Networks began approximately 50 years ago, inspired by a desire to understand the human brain and emulate its functioning. Within the last two decades, it has experienced a huge resurgence due to the development of more sophisticated algorithms and the emergence of powerful computation tools. It has been proved that ANN models show better results in river stage-discharge modelling in comparison to traditional models. The human brain always stores the information as a pattern. Any capability of the brain may be viewed as a pattern recognition task. The high efficiency and speed with which the human brain processes the patterns inspired the development of ANN and its application in field of pattern recognition. ANN is a computing model that tries to mimic the human brain and the nervous system in a very primitive way to emulate the capabilities of the human being in a very limited sense. ANNs have been developed as a generalization of mathematical models of human cognition or neural biology. Comparison to a conventional statistical stage-discharge model shows the superiority of an approach using ANN. Basic principle of ANN is shown in Fig. 1.
Enlargement of ANN is based on the following rules:
1. Information processing occurs at nodes that are single elements and are also denoted as units, neurons or cells.
2. Signals are passed between nodes through connection links.
3. Each connection link has an associated weight that represents its connection strength.
4. Each node typically applies a nonlinear transformation called an activation function to its net input to determine its output signal.
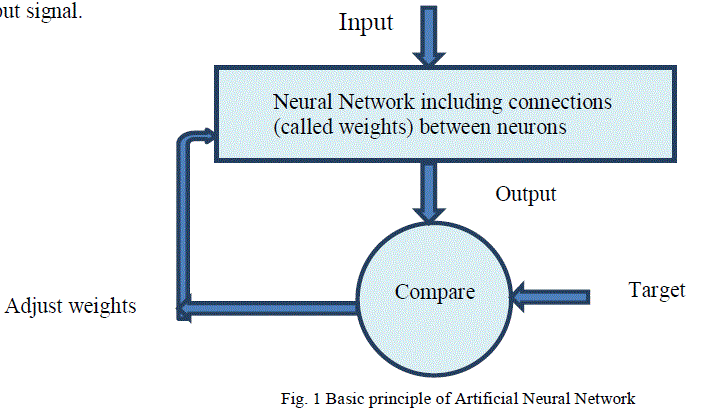image
ANN is network of parallel, distributed information processing system that relates an input and output vectors. It has a quantity of information processing elements such as cells or nodes and that are grouped in layers. The input layer processing elements receive the input vector and transmit the values to the next layer of processing elements across connections where this process is continued. This type of network, where data flow one way (forward), is known as a feedforward back propagation network. A feedforward back propagation ANN has mainly input layer, an output layer, and one or more hidden layers between the input and output layers. Each of the neurons in a layer is connected to all the neurons of the next layer, and the neurons in one layer are connected only to the neurons of the immediate next layer. The strength of the signal passing from one neuron to the other depends on the weight received from the interconnections. It is initiate that ANNs are robust tools for modeling many of the nonlinear hydrologic processes such as rainfall-runoff modelling, ground-water administration, water quality recreation, stream flow, and reservoir water levels. The hidden layers enhance the network’s ability to model complex functions. Performance of BPANN (Back Propagation Artificial Neural Network) models is compared with the developed linear transfer function (LTF) model and was found superior. ANNs can effectively model the stage-discharge relationship.

II. RELATED WORK
Mahmood et al. [7] used seven different combinations of input variables and trained them for release model. The principal inputs which were used to compute monthly release were monthly inflow, rainfall, evaporation, reservoir storage, monthly total demand and released water at previous time. The model which gave the highest coefficient of determination was selected to make released formula. It was found that ANNs have the ability to predict the release with accepted accuracy. The sensitivity analysis for the model indicated that the reservoir storage (t) has the most significant effect on the predicted release water (t) followed by release water (t-1). The result also indicated that rainfall, monthly total demand have moderate impact, while evaporation and inflow have the smallest impact. Okoye and Igboanugo [9] successfully developed a sound and statistically robust methods and models and the aim of this study was to develop artificial neural network models for predicting water levels at kanji dam, which supplies water to Nigeria’s largest hydropower generation station. It involves taking of a ten year record of the daily water levels at the dam. The daily water level were used to develop five neural network models and an Autoregressive Integrated Moving Average (ARIMA) model to fit the daily water levels obtained. The results show that the prediction accuracy of the neural network model increases with increasing input, but after the four – input model the accuracy started declining. The four – input neural network model had the lowest relative error while the single input model had the highest relative error. Generally, the models’ predictions were good, but the neural network models which involve little mathematics were much simpler to build. The developed models were very useful in power planning in Nigeria’s hydropower stations for more efficient power supply. Ondimuand Murase [10] observed that the neural networks (NN) models developed in the study were able to forecast the water levels of LakeNaivasha for four consecutive months beginning after agiven month and given data for six consecutive monthsprior to that month. Thus, NN provide an effective andtimely method for forecasting water levels in the lake.This can help in water-use formulation and schedulingfor domestic, municipal and agricultural uses. Timelyforecasting can also help in disaster monitoring,response and control in areas prone to floods. Forpower generation, effective and timely reservoir levelforecasting can help in predicting power loads andmanagement of power generation for efficiency andoptimization.The number of feature groups and the number ofelements in each feature group used as inputs greatlyinfluence the ability of NN to forecast reservoir levelsaccurately.Data compression using the Karhunen–Loeve Transform(KLT) provides an optimal technique of reducingthe size of input vectors and thus reduces the size of NNused. This greatly increases the forecasting ability of theNN models. However, data compression introducesundesirable qualities into the data that affects theforecasting ability of the NN. In addition, overcompressionof data undermines the efficiency of NNin forecasting reservoir levels.

III. STUDY AREA
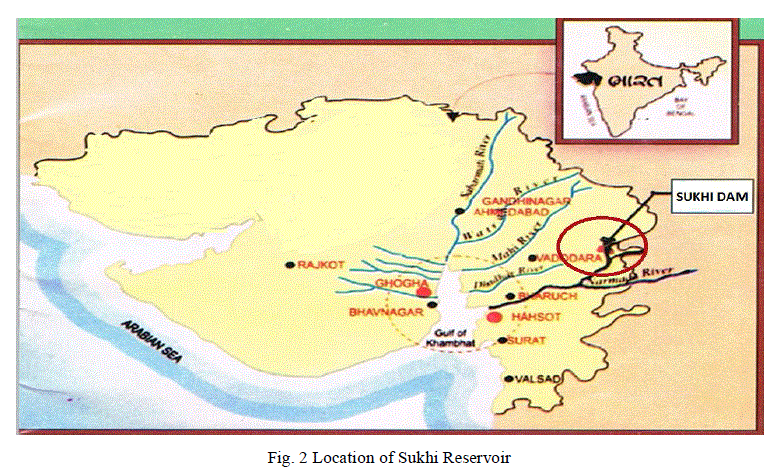
The study area isSukhi Reservoir project, it is a part of the major Water Resources projects envisaged, constructed and developed by Govt. of Gujarat at the confluence of river Sukhi and Bharaj river near village Sagadhra and Khos in Pavijetpur and Chhota-UdepurTaluka of Vadodara District in Gujarat State, India and it lies between longitudes of 73˚ 53’ 00” E and latitudes of 22˚ 26’ 00” N. The location of Sukhi Reservoir is shown in Fig. 2.
image
The region experiences a typical semi-arid climate (aridity index 15-20%); the average annual rainfall is 700-1000 mm with 30 to 45 rainy days and has dependability of 50-60%. Mean annual temperature is 26-270 ˚C with mean maximum and minimum temperatures of 410 ˚C and 110 ˚C respectively and the range of extremes is 460 ˚C to 500 ˚C. The average annual wind speed is 5 to 15km/hr. Interestingly a pocket in Panchmahals experiences, a high wind velocity of more than 15 km/hr. Winds blow from West and South-West for most part of the year. The average relative humidity is 60-65 %. The potential evapotranspiration is about 2250 mm. The Climate of Vadodara station is semi-arid with fairly dry and hot summer. Winter is fairly cold and sets in, the month of November and continues till the middle of February. Summer is hot and dry which commences from mid of February and ends by the month of June. Monsoon sets in around end of June to mid-July.

IV. METHODOLOGY
The whole data set comprises of total of 23 years, out of which 16 years data was used for training and rest of the 07 years of were used for validating the models. Forecasting was done by evaluating the model fitness and performance in 10 days ahead forecasting. The desired outputs were the Water levels corresponding to the 10 days ahead forecast. Inputs were feature group elements of inflow, water level and release.
The testing patterns are used for evaluating accuracy of the ANN trained model that is developed using ANN. Several patterns of input data have been employed to develop the optimum ANN model for the reservoir Water level. Three different NN models; Cascade, Elman and Feedforward back propagation were developed. A three-layered architecture with 10 neurons in the hidden layer and one neuron in the output layer was adapted for all the models after trial and error. The number of neurons in the input layer varied with the number of elements in the input vector for each model. Three elements from each feature group were joined to the input vector elements by the relation given in equation (1).
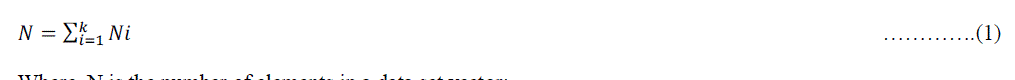image
First, real time information has got to be inheritable from reservoirs through the file based mostly date transfer system like SFTP or transfer over by emails manually. It includes daily information should also be added along with historical information over amount of time into the database. Behavioural research and end-use analysis require not just information but also the context for energy use. These slow dynamical datasets should be updated regularly, and also the modification of sources over time should be done themselves. As a result, an automatic information ingest system has got different sizes as well as rates to support discrete information acquisition, and be approachable for necessities and different information sources.
Data inherited is kept into the temporary storage and afterwards has got to be keep and shared with comparatively large system. To researchers mining and exploring information for correlations and gaining information is most vital. The information collaboration has got to be balanced against the considerations of knowledge security.
Data-driven forecasting models are essential and for it data-driven models are trained using the existing data, and utilize large-scale options that are direct and indirect indicators of water levels. In particular, our demand foretelling models use ANN time-series to supply high accuracy, uses the feedforward back propagation for playacting such analytics.
The greatest advantage of data-driven models is that the convenience of automatically building a model without having deep technical information on the system. The models also can be easily well-kept up to now by grooming them over new data that is collected. Further, it permits data analysts to try completely different combos of options to find those that most significantly impact the water levels. This can help to outline the limits for data collection, or alternatively can provide us the ways to reduce usage of water. This tends to noticethat there's no one size fits alluniversal model, and a set of models are used for various functions, however the results of exploitation ANN model provides most as regards to actual results.
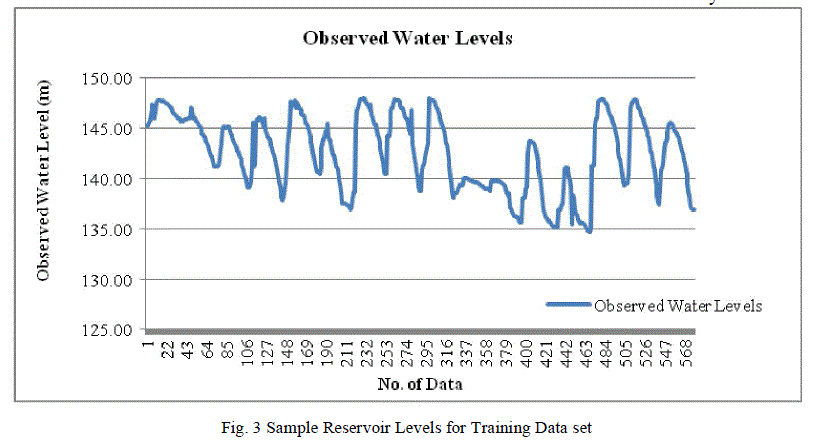
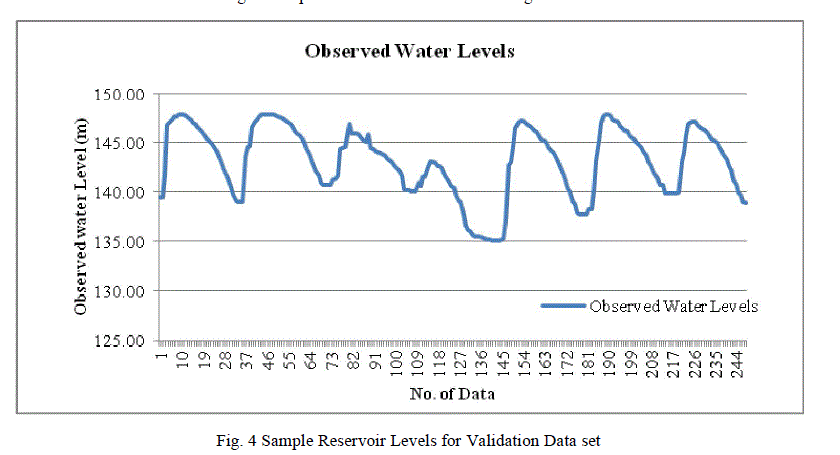
The information of the water level, inflow and release is collected.The level of reservoir is plotted for the info collected for the past years and to see the patterns and behaviour. Fig. 3 and Fig. 4 shows observed water level for training and validation period.It is observedthat the level volume unit are less consistent across some of theyears.
image

V. RESULT
The most important part of ANN model is its ability to forecast future events accurately. This Water level forecasting is an essential topic in water management affecting reservoir operations and effective multipurpose water storage. The statistical evaluation criteria used in the present study are Root Mean Square Error (RMSE), Correlation Coefficient (R) Coefficient of variation (R2) Coefficient of Determination (D). Table 1 shows the values of evaluation parameters for training set of data.
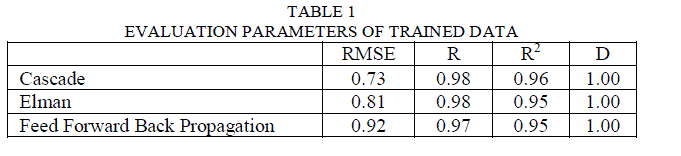image
After observing the evaluation parameters, it is observed that Feed Forward Back propagation gives the best output having RMSE; 0.92, Correlation Coefficient, R ; 0.97, Coefficient of Determination, R2 ; 0.95 and Discrepancy Ratio, D ; 1.00.
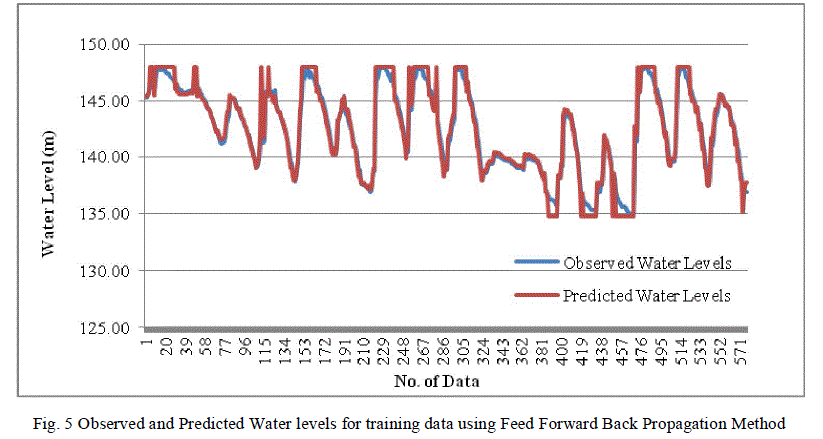
The ANN model using Feed Forward Back Propagation predicts the water levels that measure very close or near to the actual levels, as depicted in the form of graph in Fig 5 and Fig.6. Less variation measure seen with the forecasted and that of the actual provides the closeness of predication to the actual values.
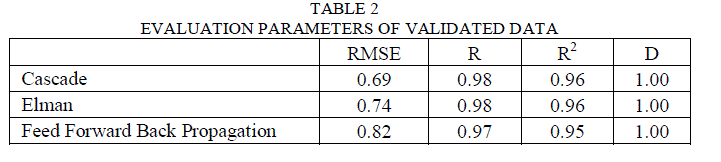
image
The forecast accuracy is validated on the remaining 30% of the data by evaluating the following statistic performance indicators: Root Mean Square Error (RMSE), Correlation Coefficient (R), Coefficient of determination (R2) and Discrepancy Ratio (D) described in Table 2.
image
Fig. 7 shows the variation of water levels between the forecasted and that of the actually observed.
image

VI. CONCLUSIONS
The neural networks (NN) models developed in this study were able to forecast the water levels of Sukhi Reservoir for ten daily consecutive days beginning after a given day and given data for ten consecutive days prior to that day. Thus, NN provide an effective and timely method for forecasting water levels in the reservoir. This can help in water-use formulation and scheduling for domestic, agricultural and municipal uses. Timely forecasting can also help in disaster monitoring, response and control in areas prone to floods. For power generation, effective and timely reservoir level forecasting can help in predicting power loads and management of power generation for efficiency and optimisation. The number of feature groups and the number of elements in each feature group used as inputs greatlyinfluence the ability of NN to forecast reservoir levels accurately.
The main conclusions obtained are as below:
1. Soft computing technique like ANN is reliable and more accurate than conventional methods.
2. On the basis of performance evaluation of models, ANN model using Feed Forward Back Propagation gave best results among three developed ANN models.
3. This paper also demonstrates that ANN technique give good results for more number of inputs.
Feed Forward Back propagation gives the best output having RMSE; 0.92, Correlation Coefficient, R;0.97, Coefficient of Determination, R2;0.95 and Discrepancy Ratio, D;1.00 in comparison of Cascade which gives the output having RMSE; 0.73, Correlation Coefficient, R; 0.98, Coefficient of Determination, R2; 0.96 and Discrepancy Ratio, D; 1.00 and Elman which gives the output having RMSE;0.81, Correlation Coefficient, R;0.98, Coefficient of Determination, R2; 0.95 and Discrepancy Ratio, D; 1.00. Based on these results, it can be concluded that amongst the three methods used for this study, ANN using Feed Forward Backpropagation is an appropriate predictor for real-time Water Level forecasting of Sukhi Reservoir Project.

References
  1. Alvisi S, Mascellani G, Franchini M and Bardossy A, “Water level forecasting through fuzzy logic and artificial neural network approaches”, Hydrology and Earth System Sciences, 10, 1–17, 2006 www.copernicus.org/EGU/hess/hess/10/1/SRef-ID: 1607-7938/hess/2006-10-1 European Geosciences Union, 2006.
  2. ASCE, “Task Committee on Application of artificial neural networks in Hydrology” (2000), Artificial neural networks in Hydrology II: Hydrologic Applications, Journal of Hydrologic Engineering, ASCE, vol. 5, no. 2, pp. 124–137, 2000.
  3. Bhattacharya B. and Solomatine D. P., “Application of artificial neural network in stage discharge relationship”, in Proceedings of the 4th Int. Conf. on Hydro-informatics, Iowa, USA, 2000.
  4. Bisht D. C. S., M. M. Raju, M. C. Joshi, “ANN based river stage-Discharge modelling for Godavari river, India”, Computer Modelling and New Technologies, vol. 14, no. 3, pp. 48-62, 2010.
  5. Golabi M, Radmanesh F,Akhondali A and Kashefipoor M., “Prediction of Seasonal Precipitation Using Artificial Neural Networks (Case Study: Selected Stations of (Iran) Khozestan Province), ISSN 2090-4304, Journal of Basic and Applied Scientific Research”, 2013.
  6. Jain S. K. and Chalisgaonkar , “Setting up stage-discharge relations using ANN”, Journal of Hydrologic Engg., vol. 5, no. 4, pp. 428-433.[6] Box, G.E.P., Jenkins, G.M. and Reinsel, G.C. Time Series Analysis Forecasting and Control. McGraw-Hill Inc., USA, 1994.
  7. Mahmood, Mustafa and Muhammed, “Application of Artificial Neural Networks to Forecast theRelease Water from Haditha Dam”, Special Issue of Engineering and Development Journal ISSN 1813-7822, 2012.
  8. McCulloh and Pitts, “Logical Calculus of ideas immanent in nervous activity”, Bulletin of Mathematical Biophysics, vol. 5, pp. 115-133, 1943.
  9. Okoye N. and Igboanugo, A.C, “Predicting Water Levels at Kainji Dam using Artificial Neural Networks”, 2013.
  10. Ondimu S. and Murase H., “Reservoir Level Forecasting using Neural Networks: Lake Naivasha”, Biosystems Engineering 96 (1), 135–138, 2007.
  11. Shrivastava, Pandiaraj and Jagadeesan,“Cloud based software platform for big data analytics in Water Reservoir Level Forecasting”, IOSR Journal of Computer Engineering (IOSR-JCE), 2014.